oo第三次博客-JML规格

这三周的作业主要是围绕以JML来约束代码开发，以确保程序的正确性与鲁棒性。

Part 1：三次作业的实现与bug

第一次作业没有任何算法和数据结构上的难度，对于Path和PathContainer的各个方法的实现按照给出的规格复读即可。唯一的难点（大约也不算难点）便是将NodeId进行映射，用hashmap就好，不过注意不要做一个调包侠，hashmap中有的方法譬如遍历很慢，虽然看上去只差常数，但是这个常数巨大，如果在第一次作业中不加处理就会在第二次作业中TLE。

第一次作业也让我们了解了抛异常，我个人认为JML对于抛异常的处理是值得称道的，通过这样的约束可以控制程序在犯了一些明显的错误后及时停止而不是越错越远浪费计算资源，造成更严重的后果。

第二次作业是在第一次的基础上写一个Graph类，这个类继承PathContainer，将不同的Path汇总成一个图，并能够查询最短路。

对于第二次作业，首先要吐槽的是给出的接口，在需要继承的情况下应该声明为protect，才能更好地实现数据的继承，而给出的接口使用了private，给我们的选择便只有重新声明数据，每当使用的时候get一次以更新或者将第一次PathContainer的代码复制到Graph中，我为了偷懒选择了后者，结果第三次就只能靠疯狂压行来改正代码风格。

对于第二次图的实现，介于图中边权均为1，求最短路和是否连通均可以使用BFS。在BFS中将查找到的点均进行更新就好，这样，在询问两点是否连通或者他们的最短路时，可以先查找对应图中两点间值是否为初始值，若是则BFS查找更新，否则直接返回结果。同时只有当需要查找两点间最短路或者连通情况且Path有过remove或add且上一次Path改变后没有更新才更新图。

对于第三次作业，其实是在求带权最短路。这里再使用BFS就不太合适了。

对于连通块数量，可以使用并查集，也可以选择图中一个点开始BFS，终止后若没有遍历所有点则选择一个未遍历的点继续BFS，如此往复至图中所有点被搜索过即可。这两者后者更快。

对于三种不同的最短路，王嘉仪同学给出的关于图的数学性质是正确的，利用这个性质我们可以更简洁的完成最短路。

以最短花费为例，设边权为1，跨路径一次消耗2，则最终消耗=边数+2*换乘数-2，此时，对于同一路径内任意两点，我们先求出图内floyd最短路图，将其中的值全部加上2，再将这些图合并后使用迪杰斯特拉求出两点间最短路，得到的值减去2就是正确答案。注意求起点a到终点b的最小花费时，使用迪杰斯特拉算法更新的点答案均是正确的，所以若是询问的两点的最短路值不是初始值就可以直接输出了。其余几种最短路可以类推。

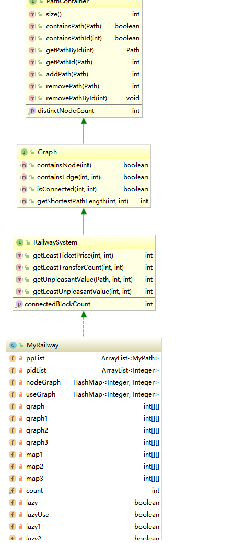
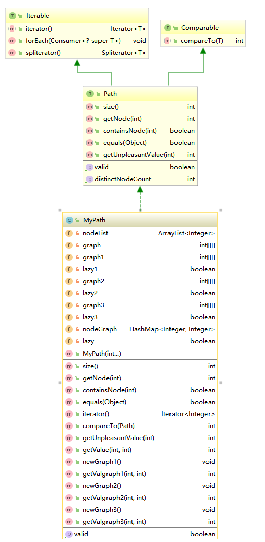
这三次作业只有最后一次有bug，我将最短路的图设置为了1000，没想到UnpleasentValue的最小值超过了1000.

关于这三次作业的不足，我觉得最大的问题在于继承复用上。因为接口里给出的类型是private，没有办法使用protected继承数据，导致继承时需要把所以数据使用时get一次，而我选择了偷懒的办法，直接将被继承的代码写入了新的代码中，这导致我第三次作业的Railway很长很丑。

Part 2：关于JML

JML(Java Modeling Language)是用于对Java程序进行规格化设计的一种表示语言。

JML能够用形式化语言来规范代码，提高代码可维护性。

JML以注释形式存在，每行以@开始，分为行注释（表示为//@......）和块注释（表示为/*@......@*/）。

JML有原子表达式，量化表达式，集合表达式等等，以及约束类型的类型规格和约束方法的方法规格。

原子表达式有\result和\old()两种，前者用来约束一个方法的返回值，后者用来表示括号内内容在方法执行前的内容。

量化表达式有forall，\exists和\sum，forall表示某范围内的元素均应满足某条件，为全称量词，相应的\exists为存在量词，而\sum返回的是给定范围内表达式的和。

集合表达式则构造一个容器，明确其包含的元素。

操作符包含子类型操作符<，等价操作符<==>，不等价操作符<=!=>，推理操作符==>，上述操作符均返回bool型值。

对于方法规格，我们通过requires语句约束前置条件，通过ensures语句约束后置条件，同时JML也给出了副作用、异常的约束，通过saaignable和modifiable来约束副作用，并利用signals来抛异常。

对于类型规格，主要利用不变式invariant P来进行约束。

部署JML UnitNG/JML Unit

安装后，编写测试样例如下：

测试结果如下：

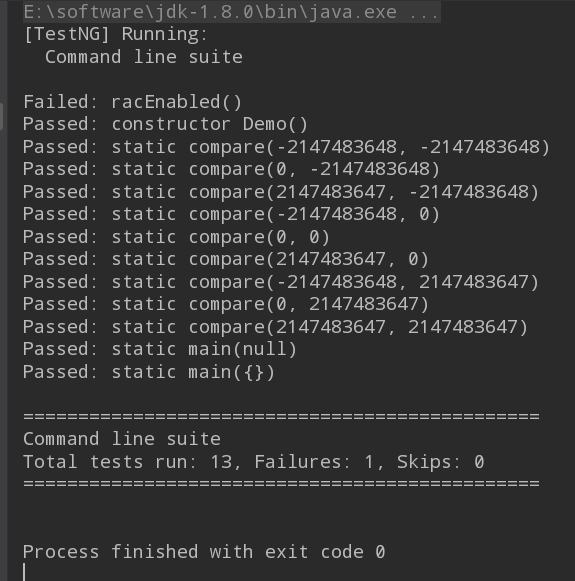
关于JML的使用，我个人感觉它只应该是一种严格的约束。事实上，我们的代码和JML都是形式化语言，而我们使用JML是为了自然语言表述不清导致代码bug。

我认为，规格应该是宏观的，整体的，针对于方法的输入输出形式，而不应该是对于代码实现的全盘描述，若是后者，那写代码岂不成为了对于规格的翻译？那我们为什么不直接写规格？规格应该是规范而不涉及具体的内部实现。

举个例子，形式化的规格语言可以作为伪代码来描述算法，我们利用这种形式化的语言来详尽的描述算法，在用java语法来翻译规格语言，这显然是在做重复无谓的工作。

在这几次作业中，尤其是最后一次作业，我们可以发现，新增的方法具有大量的规格，不少同学都吐槽过这个规格又臭又长，而我发现这些又臭又长的规格真正有用的部分是在于对于输入输出数据合法性判断以及抛异常的部分，剩下的部分其实是在表达算法思想，而我认为描述算法不应该是规格应该做的。