从零开始学算法---二叉平衡树（AVL树）

先来了解一些基本概念：

1）什么是二叉平衡树？

之前我们了解过二叉查找树，我们说通常来讲， 对于一棵有n个节点的二叉查找树，查询一个节点的时间复杂度为log以2为底的N的对数。

通常来讲是这样的， 但是。。。有例外

比如，我们向一棵树中输入预先排好序的数据， 如1，2，3，4，5，。。。10000， 可以想象到，将形成一棵斜树那么查找10000就要经过9999次比较才能得到，这显然不是我们期望看到的

所以，我们希望引入一个约束条件----任何节点的深度不得过深。

这就是二叉平衡树

二叉平衡树是二叉查找树（排序树）的一种，其每一个节点的左子树和右子树的高度差最多为1

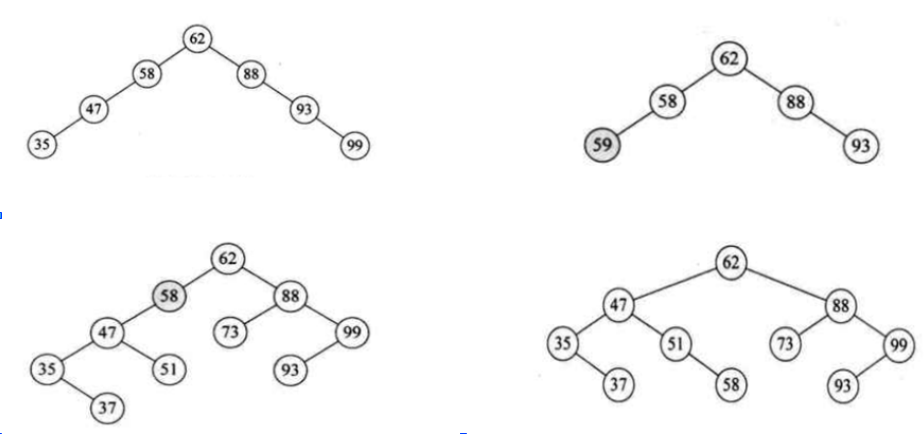
如上图， 左边两棵树并不是二叉平衡树， 因为节点58的左子树和右子树高度差>1。 （分别为2和3）

2）平衡因子？

二叉树上节点的左子树高度 减去 右子树高度， 得到的结果称为该节点的平衡因子

3）最小不平衡树？

当我们给一个二叉平衡树增加新的节点时，会产生最小不平衡树

以   距离插入节点最近的，平衡因子大于1的节点   为根的树， 我们称为最小不平衡树

如

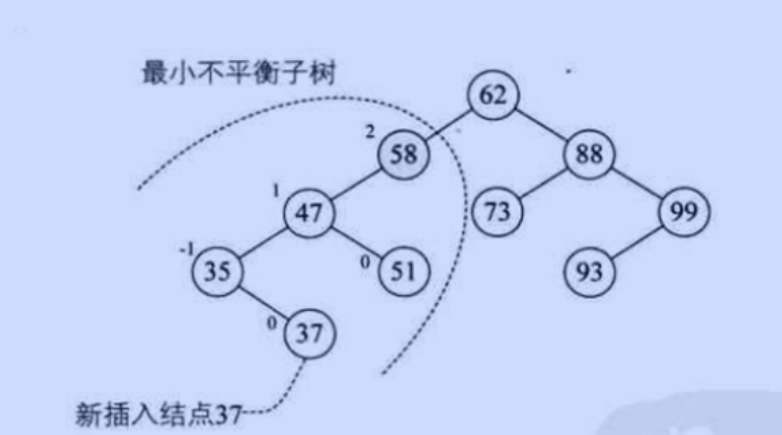
了解了基本概念之后，我们来看看如何构建一棵二叉平衡树

来看一个例子，我们从初始的空AVL树开始插入3，2，1， 当插入1时， AVL的性质在根（3）处被破坏，此时，我们需要在根与其左儿子间实施单旋转以解决这个问题

我们继续插入节点4， 这没什么问题， 但当我们插入节点5时， AVL的性质在节点3处被破坏， 因此， 我们需要在节点3与其右儿子之间实施一次左旋来解决这个问题

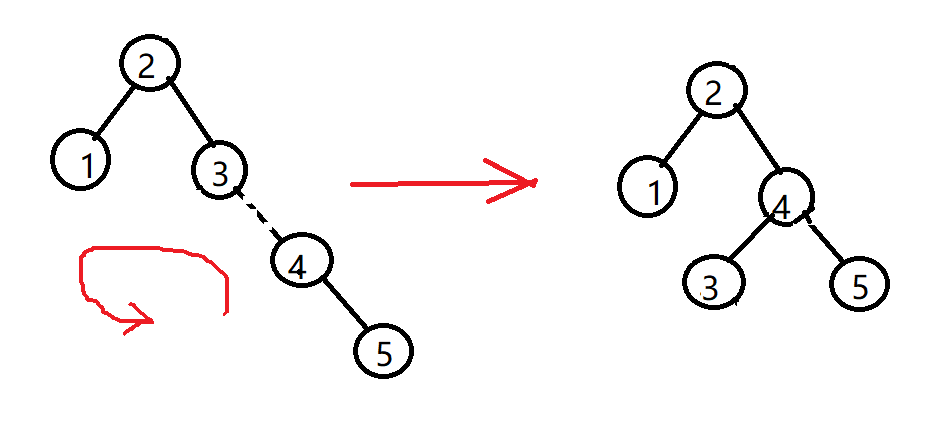
现在我们再插入节点6，此时AVL的性质在根节点（2）处被破坏， 因此我们在根节点和其右节点4之间实施一次左旋

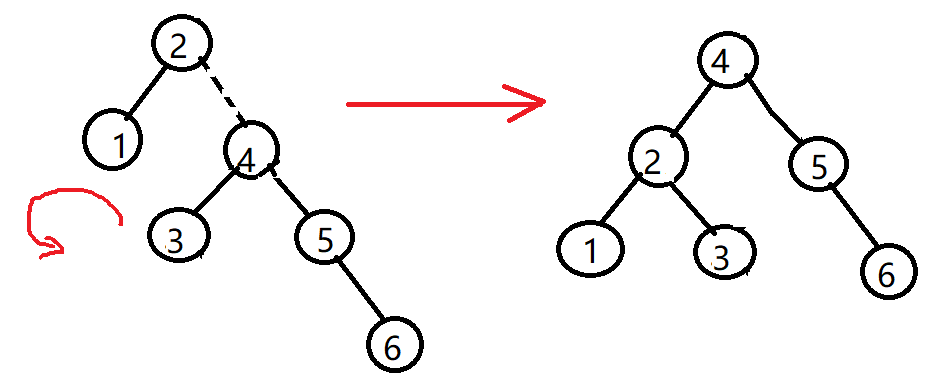
左旋的结果是 4成为根节点，2成为4的左儿子， 4 原本的左儿子3成为2的右儿子

现在再插入节点7， 此时AVL的性质在节点5处被破坏， 因此我们在5节点和其右节点6之间实施一次左旋

根据上面的操作，我们现总结处两条规律:（太绕口，不用记，看图能理解就可以）

假设当我们插入新节点时，导致了原AVL树在节点 p 处不平衡，那么

1）如果添加的新节点是p的左儿子的左儿子， 则在p和其左儿子之间实施一次右旋转， p变成其左儿子的右儿子（如果其左儿子原本已经有右儿子， 则原本的右儿子成为p的左儿子）

2）如果新加的节点是p的右儿子的右儿子， 则在p和其右儿子之间实施一次左旋转，p变成其右儿子的左儿子（如果其右儿子原本已经有左儿子， 则原本的左儿子成为p的右儿子）

感觉头都转晕了

but...真正复杂的还在后面。。。。。。。。

现在我们给上面的二叉树插入节点16，这没什么问题， 再插入15， 此时二叉树在节点7处不再平衡，这时我们发现单旋转已经不能解决问题了， 如果只是在7和16之间左旋的话，15将成为16的右节点，这显然不符合二叉排序树的性质。

因此这里我们需要两次旋转，先在15和16之间进行一次右旋，右旋之后就满足了上文规律2）的条件，此时再进行一次左旋

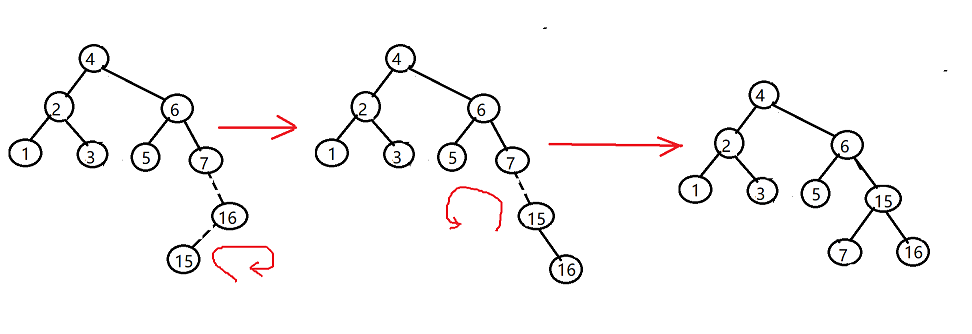
现在我们再插入14， 跟上面情况类似，插入之后需要执行先右旋再左旋的操作

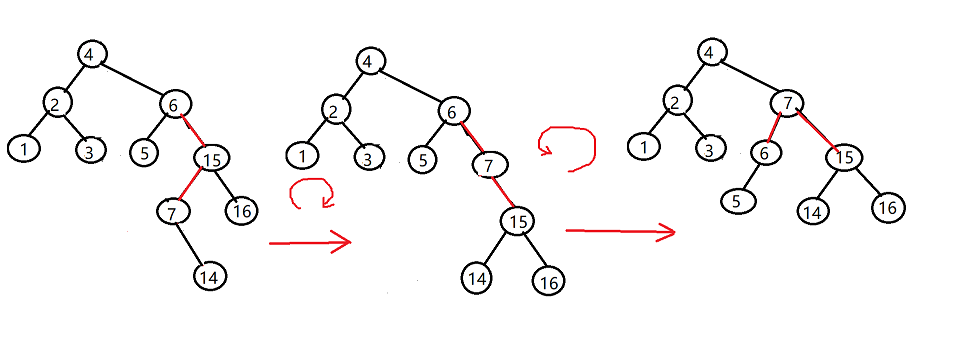
现在让我们再做个小结，

当我们插入新节点时，导致了原AVL树在节点 p 处不平衡，那么

3）如果添加的新节点是p的右儿子的左儿子， 则先在其右儿子和右儿子的左儿子之间实施一次右旋转， 再在p和其右儿子之间实施一次左旋转

3）如果添加的新节点是p的左儿子的右儿子， 则先在其左儿子和左儿子的右儿子之间实施一次左旋转， 再在p和其左儿子之间实施一次右旋转

再高度总结下： 同向时单旋转，异向时双旋转

原理就到这里了， 代码实现比较复杂，这里就不再写了，个人觉得没有必要，因为AVL树是最古老的平衡树， 我们了解其原理是为了下一步----更好的理解红黑树。