命运（经典dp）

题目连接：http://acm.hdu.edu.cn/showproblem.php?pid=2571

命运

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 13394    Accepted Submission(s): 4686

Problem Description

穿过幽谷意味着离大魔王lemon已经无限接近了！
可谁能想到，yifenfei在斩杀了一些虾兵蟹将后，却再次面临命运大迷宫的考验，这是魔王lemon设下的又一个机关。要知道，不论何人，若在迷宫中被困1小时以上，则必死无疑！
可怜的yifenfei为了去救MM，义无返顾地跳进了迷宫。让我们一起帮帮执着的他吧！
命运大迷宫可以看成是一个两维的方格阵列，如下图所示：
 
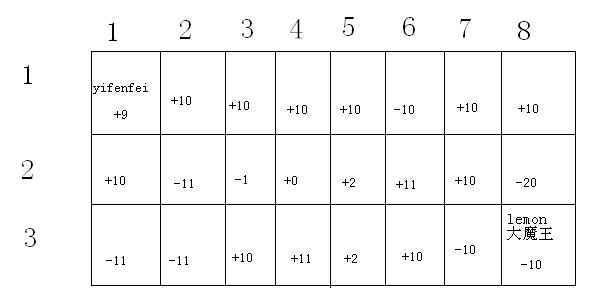
yifenfei一开始在左上角，目的当然是到达右下角的大魔王所在地。迷宫的每一个格子都受到幸运女神眷恋或者痛苦魔王的诅咒，所以每个格子都对应一个值，走到那里便自动得到了对应的值。
现在规定yifenfei只能向右或者向下走，向下一次只能走一格。但是如果向右走，则每次可以走一格或者走到该行的列数是当前所在列数倍数的格子，即：如果当前格子是（x,y），下一步可以是（x+1,y），(x,y+1)或者(x,y*k) 其中k>1。 
为了能够最大把握的消灭魔王lemon，yifenfei希望能够在这个命运大迷宫中得到最大的幸运值。

 

Input

输入数据首先是一个整数C，表示测试数据的组数。
每组测试数据的第一行是两个整数n,m，分别表示行数和列数(1<=n<=20,10<=m<=1000)；
接着是n行数据，每行包含m个整数，表示n行m列的格子对应的幸运值K ( |k|<100 )。

 

Output

请对应每组测试数据输出一个整数，表示yifenfei可以得到的最大幸运值。

 

Sample Input

1
3 8
9 10 10 10 10 -10 10 10
10 -11 -1 0 2 11 10 -20
-11 -11 10 11 2 10 -10 -10

 

Sample Output

52

 

Author

yifenfei

 

Source

ACM程序设计期末考试081230

 

题解： 这是一道经典的dp的题，但是要注意设计到倍数的跳跃的时候点的编号是从1开始的。

下面给出代码：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 #define N 25
 #define M 1010
 int mp[N][M];
 int dp[N][M];
 int main()
 {
     int t ;
     scanf("%d",&t);
     while(t--)
     {
         int n , m ;
         scanf("%d%d",&n,&m);
         for(int i = ; i <= n ; i++)
             for(int j =  ; j <= m; j++){
                 scanf("%d",&mp[i][j]);
                 dp[i][j] = -;
             }
         dp[][] = mp[][];
         for(int i = ;i <= n ;i++){dp[i][] = dp[i-][]+mp[i][];}
         for(int i = ;i <= n ;i++){
             for(int j =  ; j <= m ;j++){
                 if(dp[i][j]==-) dp[i][j] = dp[i][j-]+mp[i][j];
                 else
                 dp[i][j] = max(dp[i][j], dp[i][j-]+mp[i][j]);
                 if(i>=) dp[i][j] = max(dp[i][j],dp[i-][j] + mp[i][j]);
                 int tm = j ;
                 for(int k = ;k < tm ; k++)
                 {
                     if(tm%k==) dp[i][j] = max(dp[i][k]+mp[i][j], dp[i][j]);
                 }
             }
         }
         printf("%d\n",dp[n][m]);
     }
     return ;
 }