用于 C♯ 图像识别的轮廓分析技术

用于 C♯ 图像识别的轮廓分析技术

供稿：Conmajia

标题：Contour Analysis for Image Recognition in C#

作者：Pavel Torgashov

此中文版翻译已获作者本人授权.

Jan. 23rd，2018

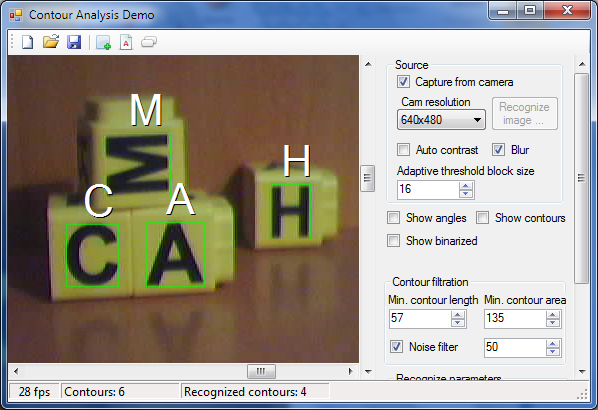
图 1 本文提供的范例程序截图

简介

本文阐述了轮廓分析 (Contour Analysis，以下简称 CA) 的理论基础以及它在图像识别方面的实际应用. 文章末尾提供了一个处理 CA 的库文件和一个范例 (参见图 1).

文章第一部分给出了 CA 的定义和相关定理. 笔者尝试尽量用精简的语言对 CA 进行概要说明，以使读者能尽快理解 CA 的理论基础并加以应用. 同时，笔者提出了一些自己的思考，试图将文章核心聚焦于 CA 理论的部分方面和算法优化上. 第二部分在此基础上对算法进行了阐述.

第三部分是对 C♯ 专用库 ContourAnalysis 的说明.

第一部分 轮廓分析基础

为什么需要轮廓分析

CA 允许对物体呈现的外部边界——即轮廓——进行描述、存储、比较和查找. 它假定此轮廓已包含有物体形状的必要信息，而不考虑物体内部的点. 对于图像，CA 将分析从 2 维空间限定到轮廓空间上可降低计算强度及算法的复杂性. 由此，CA 便可高效地解决模式识别的主要问题：图像物体的换位、旋转及重设大小. 对这些变换而言，CA 方法是不变的.

主要概念

首先，定义物体的轮廓.

轮廓是物体的边界，一组可将物体从背景中分离出来的点 (像素) 的集合.

在计算机视觉系统中，经常用到多种编码格式来记录轮廓，如 Freeman 编码、2 维编码、多项式编码等. 但在本文讲述的轮廓分析中，不使用上述任何一种编码.

作为替代，笔者使用一组复数序列对轮廓进行编码. 对某一轮廓而言，假定其上一点为起点，将该点固定. (顺时针或逆时针地) 遍历轮廓上的点，记录每个点相对于它前一个点偏移量，用复数 \(a+\mathbf{i}b​\) 表示偏移向量，\(a​\) 为 \(x​\) 轴方向上的偏移量，\(b​\) 为 \(y​\) 轴方向上的偏移量. 图 2 展示了一个简单的例子.

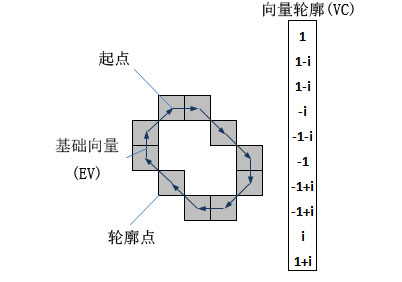
图 2 使用复数表示偏移向量

考虑到 3 维物体的物理实际，它们的轮廓不会内交，并且轮廓的最后一点总是与起点重合. 这保证了上述编码方法可以唯一地表示一个轮廓.

在这里，定义轮廓上的一个偏移向量为基础向量 (elementary vector)，简称 EV，用小写希腊字母表示；由 EV 所组成的复数序列称为向量轮廓 (vector contour)，简称 VC，用大写希腊字母表示.

这样，长度为 \(k\) 的向量轮廓 \(\Gamma\) 可以表示为：
\[
\Gamma=(\gamma_0,\gamma_1,\cdots,\gamma_{k-1})
\]
之所以采用复数编码，是因为对向量进行运算相对于其他直接计算轮廓的编码方式，在不增加额外计算负担和复杂性的基础上，可以保留可观的轮廓数学信息.

基本上，复数编码非常接近 2 维编码，后者将轮廓定义为一组 2 维空间中的坐标. 然而在处理点积上二者是不同的.

轮廓的性质

1. 闭合轮廓的所有 EV，其和为零. EV 最终指向起点，它们的和是一个零向量.
2. 轮廓向量不依赖于源图像的平行换位. 由于轮廓是相对于起点编码的，所以这种编码方式不会因初始轮廓而改变.
3. 图像旋转相当于对轮廓上所有 EV 旋转同一角度.
4. 改变起点不会改变 VC. EV 是相对于它之前的一点而编码，显然改变起点后，整个轮廓的 EV 序列除了起点位置外不会有任何改变.
5. 源图像缩放可认为是对轮廓中每个 EV 与缩放因子的乘积.

轮廓的点积

考虑轮廓 \(\Gamma\) 和轮廓 \(N\) 的点积，有：
\[
\eta=(\Gamma,N)=\sum_{n=0}^{k-1}(\gamma_n,\upsilon_n) \tag{1}
\]
其中，\(k\) 是向量轮廓 VC 的维数；\(\gamma_n\) 是轮廓 \(\Gamma\) 的第 \(n\) 个 EV；\(\upsilon_n\) 是轮廓 \(N\) 的第 \(n\) 个 EV. 复数点积 \((\gamma_n,\upsilon_n)\) 计算方法为：
\[
(a+\mathbf{i}b,c+\mathbf{i}d)=(a+\mathbf{i}b)\cdot(c-\mathbf{i}d)=ac+bd+\mathbf{i}(bc-ad) \tag{2}
\]
需要注意，在 CA 中计算轮廓的点积时，各轮廓维数必须一致，即 EV 的数量应相等.

将两个 EV 作为简单向量相乘，其点积为：
\[
\left((a,b),(c,d)\right)=ac+bd \tag{3}
\]
比较式 \((2)\) 和式 \((3)\)，可以发现：

1. 向量的点积结果为实数，复数的乘积为复数.
2. 复数点积的实数部分与对应向量的点积相等.

根据线性代数知识，向量的点积等于其夹角的余弦. 这意味着两个垂直的向量其点积总是为零，同向的两个向量其点积最大.

向量乘积的这些性质，使得它可以用来衡量向量之间的接近程度. 乘积值越大，说明向量间夹角越小，即它们越接近. 互相垂直的向量其乘积为零，随着夹角继续增大，其乘积为负值，直到再次平行时得到最大值 (绝对值). 式 \((1)\) 显然也具有与此相同的性质.

接下来引入归一化点积 (Normalized Scalar Product，NSP) 的概念：
\[
\eta=\frac{(\Gamma,N)}{|\Gamma||N|} \tag{4}
\]
模 \(|\Gamma|\) 和 \(|N|\) 计算方法为：
\[
|\Gamma|=\left(\sum_{n=0}^{k-1}|\gamma_n|^2\right)^{\frac{1}{2}} \tag{5}
\]
复数空间中的 NSP 亦为复数.

于是，NSP 归一化的最大可能值为单位向量 \(\mathbf{E}\) (|\(\mathbf{E}|=1\))，且仅在
\[
\Gamma=\mu N \tag{6}
\]
时成立. 式中 \(\mu\) 为任意复数.

我们知道，两个复数相乘，相当于它们的长度相乘 (缩放)，幅角相加 (旋转). 式 \((6)\) 中轮廓 \(\mu N\) 即表示轮廓 \(N\) 被旋转和缩放 \(\mu\) 后的结果.

所以对 NSP 而言，当且仅当轮廓 \(\Gamma\) 和轮廓 \(N\) 为相同轮廓时——可以按一定系数旋转或缩放——其模达到最大.

如表 1 所示例子. 假设两个同样的轮廓进行点积运算，可得 \(\mathrm{NSP}=1\). 将其中一个旋转 \(90^\circ\)，可得 \(\mathrm{NSP}=0+\mathbf{i}\). 旋转 \(180^\circ\) 则得 \(\mathrm{NSP}=-1\). 于是，NSP 的实数部分给出了轮廓夹角的余弦值，而模 \(|\mathrm{NSP}|\) 恒等于 \(1\).

表 1 轮廓归一化点积的性质

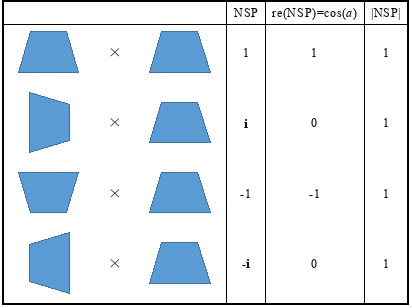
类似的，由式 \((4)\) 可知，如果增加某个向量轮廓的缩放因数，仍有 \(\mathrm{NSP}=1\).

结论 1 NSP 的模不随换位、旋转或缩放而改变.

故而仅当两个轮廓在旋转方向和缩放大小均相同时，其 NSP 为 \(\mathbf{E}\)，否则均小于 \(\mathbf{E}\). 实际上，NSP 的模与其换位、旋转或缩放等变换均无关. 类似的，如果轮廓处于变化中，则它们的 NSP 必小于 \(\mathbf{E}\).

结论 2 NSP 的模体现了轮廓之间的接近程度.

轮廓的相关函数

上一节，我们确立了 NSP 在轮廓相似性判断中的作用. 然而要使用这一性质，取决于对起点的选取.

式 \((6)\) 仅当轮廓的起点一致时成立. 如果轮廓唯一，但 EV 所参考的起点不同，则其 \(\mathrm{NSP}\ne\mathbf{E}\).

下面引入一个新的概念，两个轮廓的内相关函数 (intercorrelation function，ICF)：
\[
\tau(m)=(\Gamma,N^{(m)}), \qquad m=0,1,\cdots,k-1 \tag{7}
\]
式中 \(N^{(m)}\) 是轮廓 \(N\) 循环移位 \(m\) 次得到的 EV.

例如，\(N=(n_1,n_2,n_3,n_4)\)，\(N^{(1)}=(n_2,n_3,n_4,n_1)\)，\(N^{(2)}=(n_3,n_4,n_1,n_2)\).

ICF 揭示了轮廓 \(\Gamma\) 和轮廓 \(N\) 在移位 \(m\) 次时的相似程度. 它是 \(k\) 的周期函数，所以我们限制 \(m\in[0,k-1]\). 显然有：
\[
\tau_{\mathrm{max}}=\max\left(\frac{\tau(m)}{|\Gamma||N|}\right),\qquad m=0,1,\cdots,k-1 \tag{8}
\]
综上，模 \(|\tau_{\mathrm{max}}|\) 表示了两个轮廓的相似度，并当轮廓相同时，\(|\tau_{\mathrm{max}}|=\mathbf{E}\). 夹角 \(\arg(\tau_{\mathrm{max}})\) 给出了一个轮廓相对另一个的夹角.

结论 3 ICF 模最大值表示了两个轮廓的相似度.

结论 4 ICF 模的最大值不受换位、缩放、旋转或起点移位的影响.

另一个新概念是自相关函数 (autocorrelation function，ACF). ACF 实际是 ICF 在 \(\Gamma=N\) 时的特例，有：
\[
\upsilon(m)=(\Gamma,\Gamma^{(m)}),\qquad m=0,1,\cdots,k-1 \tag{9}
\]
下面考察 ACF 的性质.

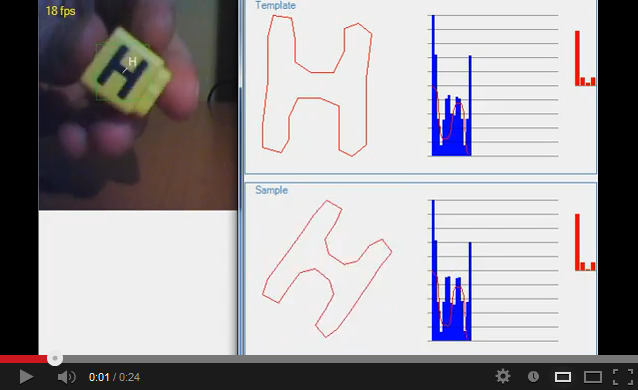
图 3 自相关函数的性质

1. ACF 与轮廓起点选取无关. 由式 \((1)\) 可知，起点的变化不会导致 \(\eta\) 改变，

2. ACF 由轮廓 EV 两两相乘得到，在 \(0\) 到 \(k\) 范围内对称分布，对称点为 \(k/2\).

令 \(N=(n_1,n_2,n_3,n_4)\)，可以写出其对不同 \(m\) 的 ACF：

\(\mathrm{ACF}(0)=(n_1,n_1)+(n_2,n_2)+(n_3,n_3)+(n_4,n_4)\)

\(\mathrm{ACF}(1)=(n_1,n_2)+(n_2,n_3)+(n_3,n_4)+(n_4,n_1)\)

\(\mathrm{ACF}(2)=(n_1,n_3)+(n_2,n_4)+(n_3,n_1)+(n_4,n_2)\)

\(\mathrm{ACF}(3)=(n_1,n_4)+(n_2,n_1)+(n_3,n_2)+(n_4,n_3)\)

\(\mathrm{ACF}(4)=(n_1,n_1)+(n_2,n_2)+(n_3,n_3)+(n_4,n_4)\)

可知 \(\mathrm{ACF}(1)=\mathrm{ACF}(3)^*\)，\(\because |a^*|=|a|\)，\(\therefore |\mathrm{ACF}(1)|=|\mathrm{ACF}(3)|\).

类似的，\(|\mathrm{ACF}(0)|=|\mathrm{ACF}(4)|\).

1. 由图 4 可以看出，除最后一幅图像外，前 3 幅图像其 ACF——用蓝色表示——均关于 \(k/2\) 对称.

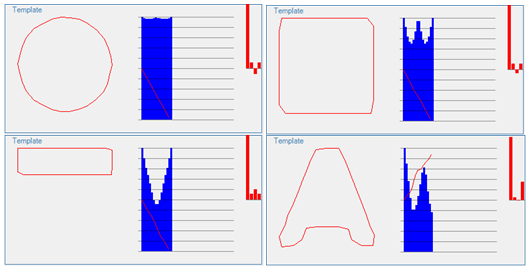
图 4 轮廓 ACF 示例

1. 在某种意义上，可以认为轮廓的 ACF 代表了轮廓的形状特性.

2. 对 ACF 取模无关于其缩放、位置、旋转或是起点的选取.

以上即是 CA 的理论部分. 在这一部分，笔者为了引入下一部分模式识别，只介绍了较为重要的相关概念和理论计算.

第二部分 轮廓分析的实际应用

通用识别算法

(未完待续)