POJ2284 That Nice Euler Circuit （欧拉公式）（计算几何 线段相交问题）

                                                      That Nice Euler Circuit

Time Limit: 3000MS		Memory Limit: 65536K
Total Submissions: 1977		Accepted: 626

Description

Little Joey invented a scrabble machine that he called Euler, after the great mathematician. In his primary school Joey heard about the nice story of how Euler started the study about graphs. The problem in that story was - let me remind you - to draw a graph on a paper without lifting your pen, and finally return to the original position. Euler proved that you could do this if and only if the (planar) graph you created has the following two properties: (1) The graph is connected; and (2) Every vertex in the graph has even degree.

Joey's Euler machine works exactly like this. The device consists of
a pencil touching the paper, and a control center issuing a sequence of
instructions. The paper can be viewed as the infinite two-dimensional
plane; that means you do not need to worry about if the pencil will ever
go off the boundary.

In the beginning, the Euler machine will issue an instruction of the
form (X0, Y0) which moves the pencil to some starting position (X0,
Y0). Each subsequent instruction is also of the form (X', Y'), which
means to move the pencil from the previous position to the new position
(X', Y'), thus draw a line segment on the paper. You can be sure that
the new position is different from the previous position for each
instruction. At last, the Euler machine will always issue an instruction
that move the pencil back to the starting position (X0, Y0). In
addition, the Euler machine will definitely not draw any lines that
overlay other lines already drawn. However, the lines may intersect.

After all the instructions are issued, there will be a nice picture
on Joey's paper. You see, since the pencil is never lifted from the
paper, the picture can be viewed as an Euler circuit.

Your job is to count how many pieces (connected areas) are created on the paper by those lines drawn by Euler.

Input

There
are no more than 25 test cases. Ease case starts with a line containing
an integer N >= 4, which is the number of instructions in the test
case. The following N pairs of integers give the instructions and appear
on a single line separated by single spaces. The first pair is the
first instruction that gives the coordinates of the starting position.
You may assume there are no more than 300 instructions in each test
case, and all the integer coordinates are in the range (-300, 300). The
input is terminated when N is 0.

Output

For each test case there will be one output line in the format

Case x: There are w pieces.,

where x is the serial number starting from 1.

Note: The figures below illustrate the two sample input cases.

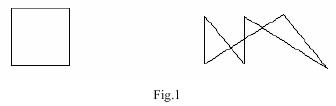
Sample Input

5
0 0 0 1 1 1 1 0 0 0
7
1 1 1 5 2 1 2 5 5 1 3 5 1 1
0

Sample Output

Case 1: There are 2 pieces.
Case 2: There are 5 pieces.
欧拉公式：对任意平面图，顶点数n，边数m且含有r个区域，则有 n-m+r=2.这题最难得还是判断两线段是否相交并求出相交点。

#include<cstdio>
#include<cstring>
#include<stdlib.h>
#define inf 0xffffff
#include<iostream>
#include<cmath>
#define NUM 22
#include <algorithm>
using namespace std;

const double eps=1e-;
struct point {
    double x,y;
    point(double a=,double b=) {
        x=a;
        y=b;
    }
};
bool operator< (point a, point b) {
    return a.x<b.x||a.x==b.x&&a.y<b.y;
}
bool operator == (point a,point b) {
    return abs(a.x-b.x)<eps&&abs(a.y-b.y)<eps;
}
struct Lineseg {
    point s,e;
    Lineseg(point a, point b) {
        s=a;
        e=b;
    }
};
struct Line {
    double a,b,c;
};
bool online(Lineseg L,point p) { //判断p是否在线段L上
    return abs((L.e.x-L.s.x)*(p.y-L.s.y)-(p.x-L.s.x)*(L.e.y-L.s.y))<eps&&(p.x-L.s.x)*(p.x-L.e.x)<eps&&(p.y-L.s.y)*(p.y-L.e.y)<eps;
}
Line Makeline(Lineseg tmp) { //线段L变成L
    Line L;
    int x1=tmp.s.x;
    int y1=tmp.s.y;
    int x2=tmp.e.x;
    int y2=tmp.e.y;
    if(y2-y1>) {
        L.a=(y2-y1);
        L.b=(x1-x2);
        L.c=(x2*y1-x1*y2);
    } else {
        L.a=(y1-y2);
        L.b=(x2-x1);
        L.c=(x1*y2-x2*y1);
    }
    return L;
}
bool Lineinter(Line x,Line y,point &q) { //直线X,Y相交于点q
    double d=x.a*y.b-y.a*x.b;
    if(abs(d)<eps)
        return false;
    q.x=(y.c*x.b-x.c*y.b)/d;
    q.y=(y.a*x.c-x.a*y.c)/d;
    return ;
}

bool Lineseginter(Lineseg aa,Lineseg bb,point &q) { //线段aa，bb如果相交则返回交点q
    Line a,b;
    a=Makeline(aa);
    b=Makeline(bb);
    if(Lineinter(a,b,q))
        return online(aa,q)&&online(bb,q);
    else
        return false;
}
bool cmp(point a ,point b) {
    if(a.x==b.x)
        return a.y<b.y;
    else
        return a.x<b.x;
}
point p[];
point inter[];
int N;
int main() {
    int m,n;
    int T=;
    while(scanf("%d",&N),N) {
        m=n=;
        int cnt=;
        for(int i=; i<N; i++)
            scanf("%lf %lf",&p[i].x,&p[i].y);
        for(int i=; i<N; i++) {
            for(int j=; j<N; j++) {
                Lineseg L1(p[i],p[(i+)%N]),L2(p[j],p[(j+)%N]);
                point q;
                if(Lineseginter(L1,L2,q))
                    inter[cnt++]=q;
            }
        }
        sort(inter,inter+cnt,cmp);
        n=unique(inter,inter+cnt)-inter;//去重复的点
        for(int i=; i<n; i++) {
            for(int j=; j<N; j++) {
                Lineseg t(p[j],p[(j+)%N]);
                if(online(t,inter[i])&&!(t.s==inter[i]))m++;
            }
        }
        T++;
        printf("Case %d: There are %d pieces.\n",T,m+-n);//欧拉定理
    }
    return ;
}