hdu 3572 Task Schedule（最大流）2010 ACM-ICPC Multi-University Training Contest（13）——Host by UESTC

题意：

告诉我们有m个任务和k个机器。第i个任务需要ci天完成，最早从第ai天开始，最晚在第bi天结束。每台机器每天可以执行一个任务。问，是否可以将所有的任务都按时完成？

输入：

首行输入一个整数t，表示共有t组数据。

接下来，每组数据第一行输入两个整数k，m，表示共有k项任务，m台机器。

接下来k行，每行包括三个整数ci，ai，bi。

输出：

如果可以完成所有任务，输出——Case i: Yes

否则，输出——Case t: No

注意，每组输出占2行

这道题我如何也想不到是个最大流。即使我知道这是最大流，我也想不出来如何建图。看了题解后，才恍然大悟。

题解：

首先建立一个超级源点0.

从1到k表示k项任务的节点，ki表示第i项任务。

从k+1到m+k表示机器的节点，第k+mi表示第mi台机器。

从m+k+1到m+k+l表示时间的节点。第m+k+li表示第li天。

最后一个超级汇点m+k+l+1。

然后从0到ki用ci连接——mp[0][ki] = ci; 表示第ki项任务需要执行ci天。

从ki到m+k+lj用1连接——mp[ki][m+k+lj] = 1; 表示第ki项任务在第lj天执行一天。

从m+k+lj到k+mi用1连接——mp[m+k+lj][k+mi] = 1; 表示第lj天使用了mi一天。

然后从k+mi到m+k+l+1用l连接——mp[k+mi][m+k+l+1] = l; 表示第mi台机器最多可以使用l天。

接下来将这张图进行运算。如果最大流等于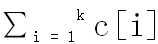，则可以完成。

同样使用Dinic算法。

上代码——

 #include <cstdio>
 #include <cmath>
 #include <cstring>
 #include <algorithm>
 #include <queue>
 using namespace std;

 const int N = ;
 const int M = ;

 int mp[N][N];
 int dis[N];
 int cur[N];
 bool vis[N];
 int t, k, m, n, l, ans, sum;

 inline int Min(int x, int y)
 {
     return x < y ? x : y;
 }

 void init()             //神奇的建图
 {
     scanf("%d%d", &k, &m);
     l = ;
     sum = ;
     memset(mp, , sizeof(mp));
     for(int i = ; i <= k; i++)
     {
         int a, b, c;
         scanf("%d%d%d", &c, &a, &b);
         if(l < b) l = b;
         mp[][i] = c;
         sum += c;
         for(int j = a; j <= b; j++)
         {
             mp[i][k+m+j] = ;
         }
     }
     n = k+m+l+;
     for(int i = ; i <= m; i++)
     {
         for(int j = ; j <= l; j++) mp[m+k+j][k+i] = ;
         mp[k+i][n] = l;
     }
     ans = ;
 }

 bool bfs()
 {
     memset(vis, , sizeof(vis));
     queue<int> que;
     que.push();
     vis[] = ;
     dis[] = ;
     while(!que.empty())
     {
         int k = que.front();
         que.pop();
         for(int i = ; i <= n; i++)
         {
             if(!vis[i] && mp[k][i] > )
             {
                 vis[i] = ;
                 dis[i] = dis[k]+;
                 que.push(i);
             }
         }
     }
     return vis[n];
 }

 int dfs(int x, int val)
 {
     if(x == n || val == ) return val;
     int flow = , minn;
     for(int& i = cur[x]; i <= n; i++)
     {
         if(dis[x]+ == dis[i] && (minn = dfs(i, Min(val, mp[x][i]))) > )
         {
             mp[x][i] -= minn;
             mp[i][x] += minn;
             val -= minn;
             flow += minn;
             if(val == ) break;
         }
     }
     return flow;
 }

 void work()         //开始搜图，即使用Dinic算法
 {
     while(bfs())
     {
         for(int i = ; i <= n; i++) cur[i] = ;
         ans += dfs(, M);
     }
 }

 void outit(int tm)
 {
     printf("Case %d: ", tm);
     if(ans == sum) printf("Yes\n\n");
     else printf("No\n\n");
 }

 int main()
 {
     //freopen("test.in", "r", stdin);
     scanf("%d", &t);
     for(int tm = ; tm <= t; tm++)
     {
         init();
         work();
         outit(tm);
     }
     return ;
 }

只是别人使用15ms，我用300+ms。看来还是需要优化啊。