Leetcode题目39.组合总和（回溯+剪枝-中等）

题目描述：

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。 
示例 1:

输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]

示例 2:

输入: candidates = [2,3,5], target = 8,
所求解集为:
[
  [2,2,2,2],
  [2,3,3],
  [3,5]
]

题目解析：(题解来自：LeetCode大佬liweiwei1419)

解题思路：
做搜索、回溯问题的套路是画图，代码其实就是根据画出的树形图写出来的。

那么如何画图呢？

根据题目中的用例，画一个图，因为是搜索，因此呈现的是一个树形结构图，并且在这个树形结构中会体现出递归结构。
根据题目中的用例，比对自己画图的结果和题目的结果的差异，如果一样，说明我们的分析没有错；如果不一样，说明我们的分析有误，一定有哪一个环节漏掉了或者分析错误，根据找到的问题调整算法。
下面我具体说一下，本来想展示草稿的，奈何本人画的图太难看，还是用软件画图给大家看吧。

针对示例 1：

输入: candidates = [2, 3, 6, 7]，target = 7，所求解集为: [[7], [2, 2, 3]]

一开始我画的图是这样的：

思路：以 target = 7 为根结点，每一个分支做减法。减到 0 或者负数的时候，剪枝。其中，减到 0 的时候结算，这里 “结算” 的意思是添加到结果集。

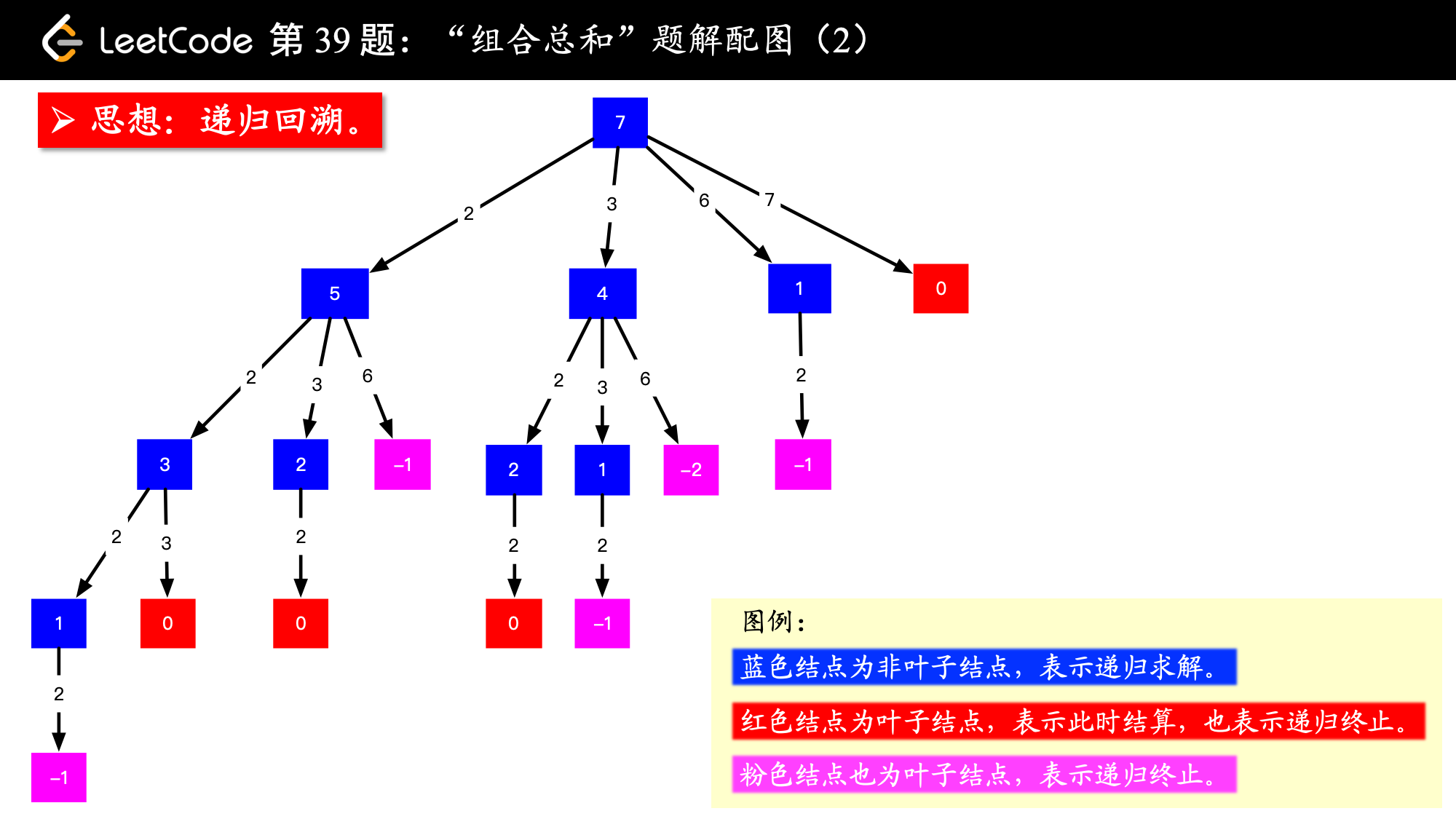
说明：

1、一个蓝色正方形表示的是 “尝试将这个数到数组 candidates 中找组合”，那么怎么找呢？挨个减掉那些数就可以了。

2、在减的过程中，会得到 0和负数，也就是被我标红色和粉色的结点：

得到 0 是我们喜欢的，从 0 这一点向根结点走的路径（很可能只走过一条边，也算一个路径），就是一个组合，在这一点要做一次结算（把根结点到 0所经过的路径，加入结果集）。

得到负数就说明这条路走不通，没有必要再走下去了。

总结一下：在减的过程中，得到 0 或者负数，就没有必要再走下去，所以这两种情况就分别表示成为叶子结点。此时递归结束，然后要发生回溯。

画出图以后，我看了一下，我这张图画出的结果有 4 个 0，对应的路径是 [[2, 2, 3], [2, 3, 2], [3, 2, 2], [7]]，而示例中的解集只有 [[7], [2, 2, 3]]，很显然，我的分析出现了问题。问题是很显然的，我的结果集出现了重复。重复的原因是

后面分支的更深层的边出现了前面分支低层的边的值。

限于我的表达能力有限，大伙意会这句话就可以了，看一看重复的叶子结点 0 的路径，想一想重复的原因，或许你会比我说得更清楚更好。

但是这个问题也不难解决，把候选数组排个序就好了（想一下，结果数组排个序是不是也可以去重），后面选取的数不能比前面选的数还要小，即 “更深层的边上的数值不能比它上层的边上的数值小”，按照这种策略，剪枝就可以去掉重复的组合。

代码实现：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Stack;

public class Solution {

    private List<List<Integer>> res = new ArrayList<>();
    private int[] candidates;
    private int len;

    private void findCombinationSum(int residue, int start, Stack<Integer> pre) {
        if (residue == 0) {
            // Java 中可变对象是引用传递，因此需要将当前 path 里的值拷贝出来
            res.add(new ArrayList<>(pre));
            return;
        }
        // 优化添加的代码2：在循环的时候做判断，尽量避免系统栈的深度
        // residue - candidates[i] 表示下一轮的剩余，如果下一轮的剩余都小于 0 ，就没有必要进行后面的循环了
        // 这一点基于原始数组是排序数组的前提，因为如果计算后面的剩余，只会越来越小
        for (int i = start; i < len && residue - candidates[i] >= 0; i++) {
            pre.add(candidates[i]);
            // 【关键】因为元素可以重复使用，这里递归传递下去的是 i 而不是 i + 1
            findCombinationSum(residue - candidates[i], i, pre);
            pre.pop();
        }
    }

    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        int len = candidates.length;
        if (len == 0) {
            return res;
        }
        // 优化添加的代码1：先对数组排序，可以提前终止判断
        Arrays.sort(candidates);
        this.len = len;
        this.candidates = candidates;
        findCombinationSum(target, 0, new Stack<>());
        return res;
    }

    public static void main(String[] args) {
        int[] candidates = {2, 3, 6, 7};
        int target = 7;
        Solution solution = new Solution();
        List<List<Integer>> combinationSum = solution.combinationSum(candidates, target);
        System.out.println(combinationSum);
    }
}