P1359 租用游艇 && P3905 道路重建 ------Floyd算法

P1359 租用游艇   原题链接https://www.luogu.org/problemnew/show/P1359

P3905 道路重建   原题链接https://www.luogu.org/problemnew/show/P3905

这两道题我觉得都是Floyd算法的应用，所以我就放在一块来写了，毕竟A这两道题的时间间隔比较短；

P1359 租用游艇

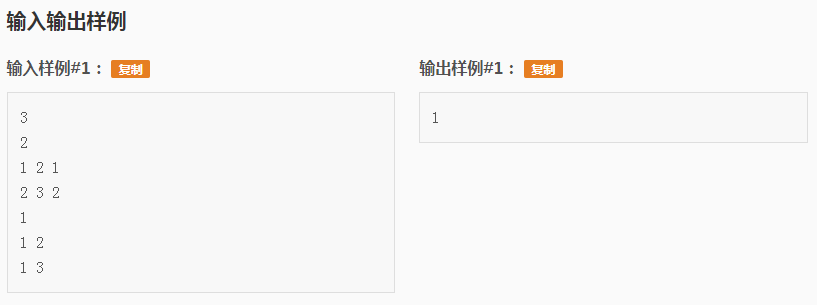
对于这个题，一开始被这个半矩阵惊到了-------主要是不知道这个矩阵是什么意思，过了好长时间（2min）才明白是到其他游艇的距离。

我们去理解一下输入：

输入半矩阵的代码：

    for(int i=;i<n;i++)
    {
        for(int j=i+;j<=n;j++)
        {
            f[i][j]=read();        //从游艇i到游艇j的距离
        }
    }

然后我们要求的就是游艇1到游艇n的距离，也就是f[1][n]，这里我们用Floyd算法就能轻松AC；

注意一个小细节：

题目中说：游客可在这些游艇出租站租用游艇，并在下游的任何一个游艇出租站归还游艇。

这句话其实是说：游艇只会顺流而下，不会逆流而上！所以我们要特判一下，如果我们枚举的中间点k<=i，直接continue；

OK上代码：

#include<iostream>
#include<cstdio>
using namespace std;
int read()
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n;
int f[][];
int main()
{
    n=read();
    for(int i=;i<n;i++)
    {
        for(int j=i+;j<=n;j++)
        {
            f[i][j]=read();        //从i到j的距离
        }
    }
    for(int k=;k<=n;k++)          //Floyd算法
    {
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=n;j++)
            {
                if(k<=i) continue; //如果枚举的中间点k在游艇i的上游，直接跳出
                if(f[i][j]>f[i][k]+f[k][j])
                f[i][j]=f[i][k]+f[k][j];
            }
        }
    }
    cout<<f[][n];                 //最后的答案
    return ;
}

P3905 道路重建

这个题其实不是很难，只是思路有些难想，我也是看了题解之后才想出来的：

这个题要你求从A到B要修的最短道路，也就是说那些没有被炸毁的道路我们不用修，我们可以将这些道路的权值赋为0，这样Floyd算法求出的最短路就是要修的最短道路，看代码：

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int read()                           //读入优化
{
    char ch=getchar();
    int a=,x=;
    while(ch<''||ch>'')
    {
        if(ch=='-') x=-x;
        ch=getchar();
    }
    while(ch>=''&&ch<='')
    {
        a=(a<<)+(a<<)+(ch-'');
        ch=getchar();
    }
    return a*x;
}
int n,m,d,f[][],vis[][]; //f数组存图，vis数组存哪条路被炸了
int main()
{
    n=read();m=read();
    for(int i=;i<=n;i++)
       for(int j=;j<=n;j++)
          f[i][j]=1e9,vis[i][j]=;   //初始化
    for(int i=;i<=m;i++)
    {
        int u=read();
        int v=read();
        int w=read();
        f[u][v]=w;                   //注意建双向图
        f[v][u]=w;
    }
    d=read();
    for(int i=;i<=d;i++)
    {
        int u=read();
        int v=read();
        vis[u][v]=;                 //表示u到v这条路被炸了
        vis[v][u]=;
    }
    for(int i=;i<=n;i++)
       for(int j=;j<=n;j++)
          if(vis[i][j]==&&f[i][j]<1e9) //如果这条路没被炸，并且连通，那么将权值设为0
             f[i][j]=;
    int s=read();
    int end=read();
    for(int k=;k<=n;k++)            //Floyd算法模板
    {
        for(int i=;i<=n;i++)
        {
            for(int j=;j<=n;j++)
            {
                if(f[i][k]+f[k][j]<f[i][j])
                f[i][j]=f[i][k]+f[k][j];
            }
        }
    }
    cout<<f[s][end];                 //起点到终点的最短修的道路
    return ;
}