【Python】【demo实验14】【练习实例】【斐波那契数列】【经典兔子生小兔子问题】

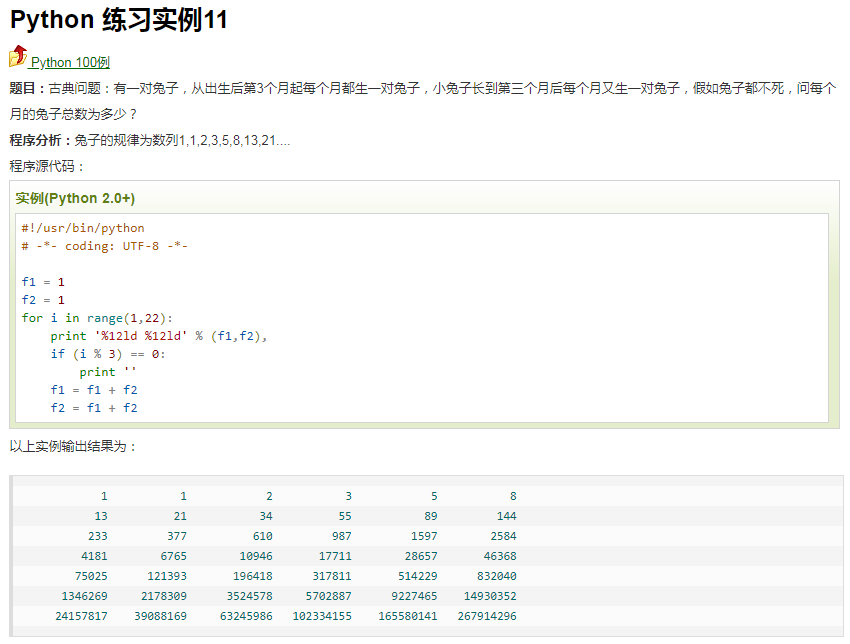
古典问题：有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问每个月的兔子总数为多少？

每个月的兔子数量

1:2
2:2
3:4 2+2
4:6 2+2+2
5:10 2+2+2+2+2
6:16 6+6+4
7:26 10+10+6

第一个月和第二个月兔子不繁殖

第三个月，两个兔子繁殖两个兔子，共四个

第四个月，两个兔子继续繁殖两个兔子，小兔子不繁殖；共6个

以此类推

2,2,4,6,10,16,26

这个数量刚好是斐波那契数列 的两倍

源代码：

#!/usr/bin/python
# encoding=utf-8
# -*- coding: UTF-8 -*-

# 斐波那契数列  兔子生兔子问题：
"""
l = []
l.append(1)
l.append(1)
while(1):
    k = len(l)
    m = (l[k-2]+l[k-1])
    print(m)
    l.append(m)
    print("====",l)

"""

# 兔子的数量

l = []
l.append(2)
l.append(2)
while(1):
    k = len(l)
    m = (l[k-2]+l[k-1])
    l.append(m)
    print("====",l)

输出结果：

原题解法：

我认为原题解法，答案不对；

　　

————————（我是分割线）————————

参考：

1. RUNOOB.COM：https://www.runoob.com/python/python-exercise-example11.html

备注：

初次编辑时间：2019年9月24日20:39:50

环境：Windows 7   / Python 3.7.2