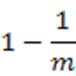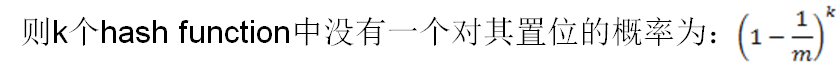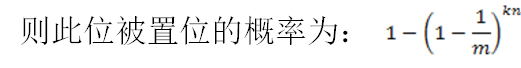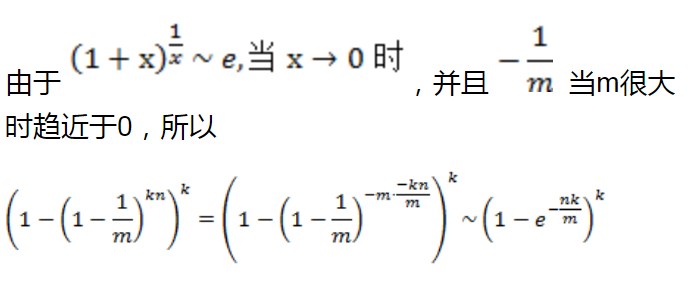OI视角浅谈布隆过滤器
简要谈及布隆过滤器
Preface
不负责的出题人扔了一道5e5,2M卡内存的题,标算布隆过滤器,然而std自己用std::set 70M碾过去了。
没学OI时候草草看过这个,不过忘得差不多了。
今天自己考试时候写的假布隆过滤器在$10^5$时候都会有10来个误判(而且这空间怎么卡啊)。
网上的资料大抵都是工程向,这里从OI角度随意谈谈布隆过滤器吧。
所谓“布隆过滤器”?
可以先浅显地理解为 低配版的多哈希 ,因为这东西的最大卖点就是空间复杂度较哈希小得多;但是正确性又不能丢太多,所以就在压缩空间的前提下多用几个哈希函数来增加正确性。
这里有一个卡空间的基础操作:bitset.因为一般的方法bool是8bit只能表示一个数的存在与否;而一个int有32bit,以位可以来表示32个数的存在。
先做说明几个变量的含义:
- $n$:总计插入$n$个元素
- $m$:实现的共有$m$位的bitset.
- $k$:有$k$个不同的hash函数,每个值域在$[0,m)$之间
其实现过程是:对于每次插入,计算得到$k$个哈希值,然后把全局的bitset这$k$个位置修改成1;每次询问,在全局的bitset里查询是否$k$个位置都是1.
没错这个东西感性理解上去就是误判率很高——对OI来说确实了。
下面一段就是课件里关于正确性证明的搬运……
假设布隆过滤器中的hash function满足simple uniform hashing假设:每个元素都等概率地hash到m个slot中的任何一个,与其它元素被hash到哪个slot无关。
(我琢磨着课件好像也是哪里copy来的)
这东西在OI里是不是没什么用
应该是的。
除了丧心病狂+不负责任的出题人会来出道布隆过滤器的题目之外,这玩意(优点:时间换空间;缺点:一定的误判率)在OI里似乎没什么用场。
END
OI视角浅谈布隆过滤器的更多相关文章
- 浅谈布隆过滤器Bloom Filter
先从一道面试题开始: 给A,B两个文件,各存放50亿条URL,每条URL占用64字节,内存限制是4G,让你找出A,B文件共同的URL. 这个问题的本质在于判断一个元素是否在一个集合中.哈希表以O(1) ...
- 细谈布隆过滤器及Redis实现
何为布隆过滤器? 本质上是一种数据结构,是1970年由布隆提出的.它实际上是一个很长的二进制向量(位图)和一系列随机映射函数(哈希函数).可以用于检索一个元素是否在一个集合中. 数据结构: 布隆过 ...
- 浅谈redis的HyperLogLog与布隆过滤器
首先,HyperLogLog与布隆过滤器都是针对大数据统计存储应用场景下的知名算法. HyperLogLog是在大数据的情况下关于数据基数的空间复杂度优化实现,布隆过滤器是在大数据情况下关于检索一个元 ...
- [技术]浅谈OI中矩阵快速幂的用法
前言 矩阵是高等代数学中的常见工具,也常见于统计分析等应用数学学科中,矩阵的运算是数值分析领域的重要问题. 基本介绍 (该部分为入门向,非入门选手可以跳过) 由 m行n列元素排列成的矩形阵列.矩阵里的 ...
- 浅谈Hybrid技术的设计与实现
前言 浅谈Hybrid技术的设计与实现 浅谈Hybrid技术的设计与实现第二弹 浅谈Hybrid技术的设计与实现第三弹——落地篇 随着移动浪潮的兴起,各种APP层出不穷,极速的业务扩展提升了团队对开发 ...
- [C#]6.0新特性浅谈
原文:[C#]6.0新特性浅谈 C#6.0出来也有很长一段时间了,虽然新的特性和语法趋于稳定,但是对于大多数程序猿来说,想在工作中用上C#6.0估计还得等上不短的一段时间.所以现在再来聊一聊新版本带来 ...
- 浅谈如何检查Linux中开放端口列表
给大家分享一篇关于如何检查Linux中的开放端口列表的详细介绍,首先如果你想检查远程Linux系统上的端口是否打开请点击链接浏览.如果你想检查多个远程Linux系统上的端口是否打开请点击链接浏览.如果 ...
- 【ASP.NET MVC系列】浅谈ASP.NET MVC 控制器
ASP.NET MVC系列文章 [01]浅谈Google Chrome浏览器(理论篇) [02]浅谈Google Chrome浏览器(操作篇)(上) [03]浅谈Google Chrome浏览器(操作 ...
- (转)浅谈Hybrid技术的设计与实现
转载地址:https://www.cnblogs.com/yexiaochai/p/4921635.html 前言 浅谈Hybrid技术的设计与实现 浅谈Hybrid技术的设计与实现第二弹 浅谈Hyb ...
随机推荐
- prometheus+grafana监控Linux和kubernetes的例子
1.安装和配置prometheus tar zxvf prometheus-.linux-amd64.tar.gz -C /usr/local/ ln -sv /usr/local/prometheu ...
- poj1741(入门点分治)
题目链接:https://vjudge.net/problem/POJ-1741 题意:给出一棵树,求出树上距离不超过k的点对数量. 思路:点分治经典题.先找重心作为树根,然后求出子树中所有点到重心的 ...
- arm-linux-ar常见用法
1) 创建test.a静态库 arm-linux-gcc -c a.o a.c arm-linux-gcc -c b.o b.c arm-linux-ar -rc test.a ...
- input框改变默认样式
input[type="radio"] { width: 2rem; height: 2rem; -webkit-appearance: none; /*清除复选框默认样式*/ ...
- ######<待随时补充>我的学习规划######
一.关于Python 1.demo 一些基础实验,包含Python基础知识等,约300-500个 2.Python常见模块的了解学习,如 time datetime random 随机数 os 与 ...
- PDO简单的DB类封装
<?php class DB{ private $dbs = ""; private $fields = "*"; private $tables = n ...
- ubuntu 系统升级
1.更新软件源和软件 $ sudo apt-get update && sudo apt-get dist-upgrade 2.安装update-manager-core $ sudo ...
- FTP-实例(Md5验证)
import socket, os, hashlib server = socket.socket() server.bind(("localhost", 9999)) serve ...
- Jmeter之JDBC取样器(数据库增删改查)
1.将数据库的jar包存入jmeter/lib目录下 2.配置jmeter 测试计划中“添加jar包” 数据库访问配置:线程组->添加->配置原件->JDBC Connection ...
- Wannafly挑战赛24
A. 石子游戏 Alice和Bob在玩游戏,他们面前有n堆石子,对于这些石子他们可以轮流进行一些操作,不能进行下去的人则输掉这局游戏.可以进行两种操作:1. 把石子数为奇数的一堆石子分为两堆正整数个石 ...