如何解决数据类别不平衡问题（Data with Imbalanced Class）

类别不平衡问题是指：在分类任务中，数据集中来自不同类别的样本数目相差悬殊。

类别不平衡问题会造成这样的后果：在数据分布不平衡时，其往往会导致分类器的输出倾向于在数据集中占多数的类别：输出多数类会带来更高的分类准确率，但在我们所关注的少数类中表现不佳。

处理这个问题通常有3种方法：

1. 欠采样

假设数据集中反例占大多数，那么去除一些反例使得正、反例数目接近，然后再进行学习。由于丢弃了很多反例，分类器训练集会远小于初始训练集。欠采样的缺点是可能会丢失一些重要信息。因此通常利用集成学习机制，将反例划分为若干个集合供不同的学习器使用，这样就相当于对每个学习器都进行了欠采样，并且从全局来看不会丢掉重要信息。

代表算法：EasyEnsemble

利用集成学习机制，将反例划分为若干个集合供不同学习器使用，这样对每个学习器来看都进行了欠采样，但在全局来看却不会丢失重要信息。

算法原理：

首先通过从多数类中独立随机抽取出若干子集。
将每个子集与少数类数据联合起来训练生成多个基分类器。
最终将这些基分类器组合形成一个集成学习系统。

EasyEnsemble 算法被认为是非监督学习算法，因此它每次都独立利用可放回随机抽样机制来提取多数类样本。

2. 过采样

假设数据集中反例占大多数，那么对训练集里的正类样例进行“过采样”，增加一些正例使得正、反例数目接近，然后再进行学习。但是不能直接对正例进行复制，这样容易引起过拟合。一般采用代表性算法SMOTE算法。它是通过对训练集里的正例进行插值来产生额外的正例。过采样的缺点是由于增加了很多正例，使得其训练集远大于初始训练集，时间开销远大于欠采样。

代表算法：SMOTE（Synthetic Minority Oversampling Technique）

通过对训练集里的正例进行插值来产生额外的正例。它利用 k 近邻算法来分析已有的少数类样本，从而合成在特征空间内的新的少数类样本。

算法原理：

SMOTE 算法是建立在相距较近的少数类样本之间的样本仍然是少数类的假设基础上的，它是利用特征空间中现存少数类样本之间的相似性来建立人工数据的。这里我们简单的介绍 SMOTE 算法的思想。

下图表示一个数据集：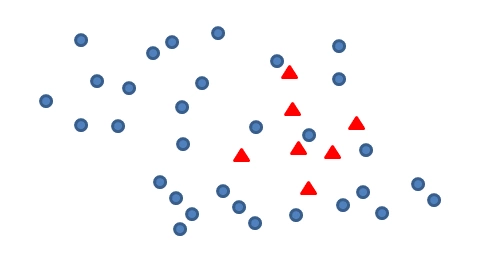

可以看出，蓝色样本数量远远大于红色样本，在常规调用分类模型去判断的时候可能会导致之间忽视掉红色样本带了的影响，只强调蓝色样本的分类准确性，因此需要增加红色样本来平衡数据集。

先随机选定 n 个少类的样本：

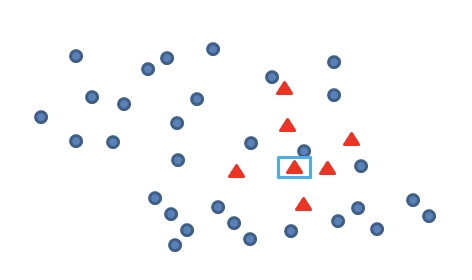
再找出最靠近它的 m 个少类样本：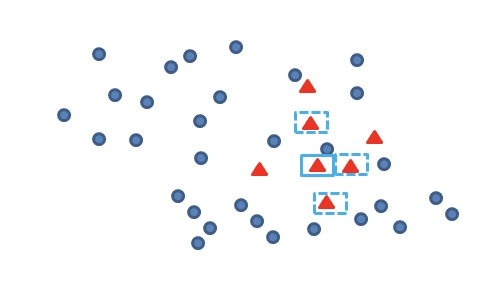

再任选最临近的 m 个少类样本中的任意一点：

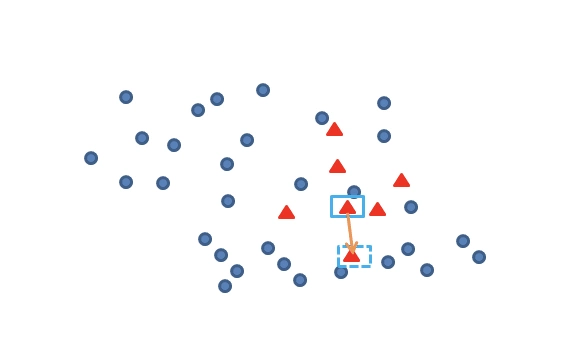
在这两点上任选一点，这点就是新增的数据样本。

3. 阈值移动

基于原始训练集进行学习，但在用训练好的分类器进行预测时，将再缩放的公式嵌入到决策过程中，称为“阈值移动”。

在二分类任务中，我们将样本属于正类的概率记为p，因此样本属于负类的概率就是1-p。当p/(1-p)>1时，我们把样本分为正类。但这是在样本均衡的情况下，也就是说正负样本的比例接近于1，此时分类阈值为0.5。如果样本不均衡，那么我们需要在预测时修改分类阈值。

假设在数据集中有m个正样本，n个负样本，那么正负样本的观测几率为m/n（样本均衡的情况下观测几率为1）。在进行分类时，如果此时的几率p'/(1-p')大于实际的观测几率m/n，我们才把样本分为正类。此时m/(m+n) 取代0.5成为新的分类阈值。