（4）ardunio 矩阵求解官方库改造，添加逆的求解

多此一举，原来官方库给了求逆的函数，在源码里

除此之外，还有转置矩阵，只不过样例没显示出来。

//Matrix Inversion Routine
// * This function inverts a matrix based on the Gauss Jordan method.
// * Specifically, it uses partial pivoting to improve numeric stability.
// * The algorithm is drawn from those presented in
//	 NUMERICAL RECIPES: The Art of Scientific Computing.
// * The function returns 1 on success, 0 on failure.
// * NOTE: The argument is ALSO the result matrix, meaning the input matrix is REPLACED
int MatrixMath::Invert(mtx_type* A, int n)
{
	// A = input matrix AND result matrix
	// n = number of rows = number of columns in A (n x n)
	int pivrow = 0;		// keeps track of current pivot row
	int k, i, j;		// k: overall index along diagonal; i: row index; j: col index
	int pivrows[n]; // keeps track of rows swaps to undo at end
	mtx_type tmp;		// used for finding max value and making column swaps

	for (k = 0; k < n; k++)
	{
		// find pivot row, the row with biggest entry in current column
		tmp = 0;
		for (i = k; i < n; i++)
		{
			if (abs(A[i * n + k]) >= tmp)	// 'Avoid using other functions inside abs()?'
			{
				tmp = abs(A[i * n + k]);
				pivrow = i;
			}
		}

		// check for singular matrix
		if (A[pivrow * n + k] == 0.0f)
		{
			Serial.println("Inversion failed due to singular matrix");
			return 0;
		}

		// Execute pivot (row swap) if needed
		if (pivrow != k)
		{
			// swap row k with pivrow
			for (j = 0; j < n; j++)
			{
				tmp = A[k * n + j];
				A[k * n + j] = A[pivrow * n + j];
				A[pivrow * n + j] = tmp;
			}
		}
		pivrows[k] = pivrow;	// record row swap (even if no swap happened)

		tmp = 1.0f / A[k * n + k];	// invert pivot element
		A[k * n + k] = 1.0f;		// This element of input matrix becomes result matrix

		// Perform row reduction (divide every element by pivot)
		for (j = 0; j < n; j++)
		{
			A[k * n + j] = A[k * n + j] * tmp;
		}

		// Now eliminate all other entries in this column
		for (i = 0; i < n; i++)
		{
			if (i != k)
			{
				tmp = A[i * n + k];
				A[i * n + k] = 0.0f; // The other place where in matrix becomes result mat
				for (j = 0; j < n; j++)
				{
					A[i * n + j] = A[i * n + j] - A[k * n + j] * tmp;
				}
			}
		}
	}

	// Done, now need to undo pivot row swaps by doing column swaps in reverse order
	for (k = n - 1; k >= 0; k--)
	{
		if (pivrows[k] != k)
		{
			for (i = 0; i < n; i++)
			{
				tmp = A[i * n + k];
				A[i * n + k] = A[i * n + pivrows[k]];
				A[i * n + pivrows[k]] = tmp;
			}
		}
	}
	return 1;
}

　　

ESP8266 07模块

首先安装库

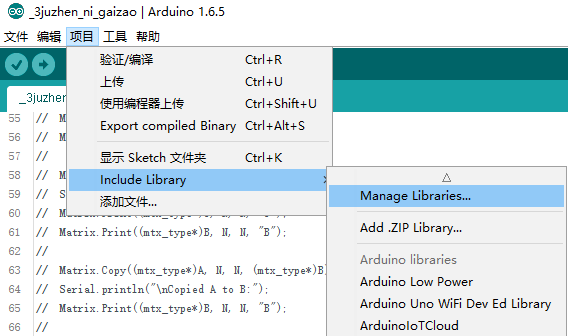
搜索

运行基本实例

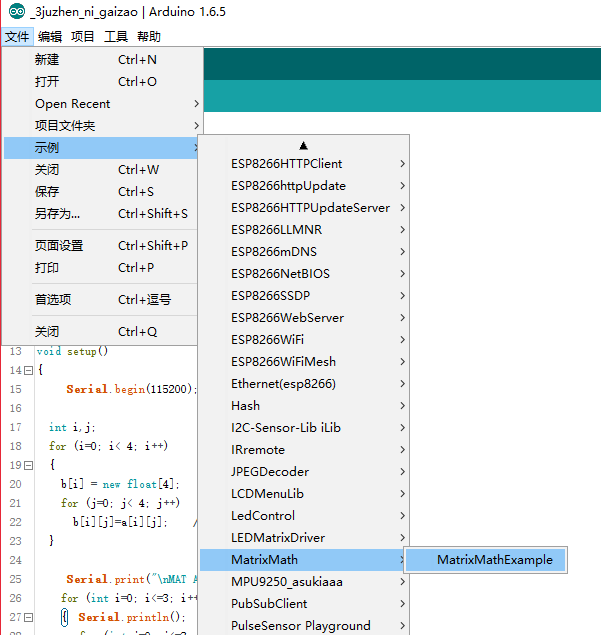
这个例子没有矩阵求逆的函数，自己添加。

使用的ESP8266芯片   07板 可外置天线

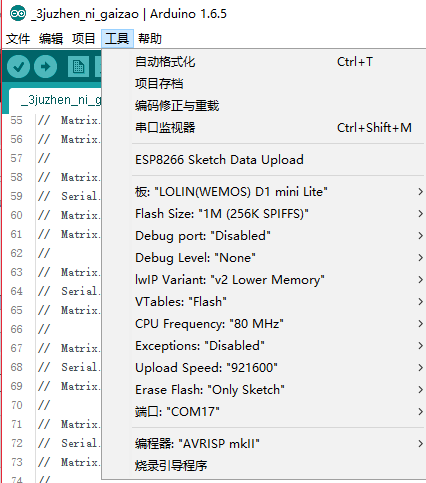
源程序

#include <MatrixMath.h>

#include "math.h"

float a[4][4]={
            {1,0,0,0},
            {1,0.5,0,0},
            {1,0,1,0},
            {1,0,0,1},
            };
float **b = new float *[4];    // 拷贝a

void setup()
{
     Serial.begin(115200);

  int i,j;
  for (i=0; i< 4; i++)
  {
    b[i] = new float[4];
    for (j=0; j< 4; j++)
      b[i][j]=a[i][j];    // 拷贝a
  }

     Serial.print("\nMAT A IS:");
    for (int i=0; i<=3; i++)
    {  Serial.println();
       for (int j=0; j<=3; j++)
       { Serial.print(a[i][j]);Serial.print("  , ");}

    }

     Matrix.NI(b,4);

    Serial.print("\nMAT A- IS:");
    for (int i=0; i<=3; i++)
    {
        Serial.println("");
      for (int j=0; j<=3; j++)
      {  Serial.print(b[i][j]);Serial.print("  , ");}

      }

}

void loop()
{

//  Matrix.Multiply((mtx_type*)A, (mtx_type*)B, N, N, N, (mtx_type*)C);
//
//  Serial.println("\nAfter multiplying C = A*B:");
//  Matrix.Print((mtx_type*)A, N, N, "A");
//
//  Matrix.Print((mtx_type*)B, N, N, "B");
//  Matrix.Print((mtx_type*)C, N, N, "C");
//  Matrix.Print((mtx_type*)v, N, 1, "v");
//
//  Matrix.Add((mtx_type*) B, (mtx_type*) C, N, N, (mtx_type*) C);
//  Serial.println("\nC = B+C (addition in-place)");
//  Matrix.Print((mtx_type*)C, N, N, "C");
//  Matrix.Print((mtx_type*)B, N, N, "B");
//
//  Matrix.Copy((mtx_type*)A, N, N, (mtx_type*)B);
//  Serial.println("\nCopied A to B:");
//  Matrix.Print((mtx_type*)B, N, N, "B");
//
//  Matrix.Invert((mtx_type*)A, N);
//  Serial.println("\nInverted A:");
//  Matrix.Print((mtx_type*)A, N, N, "A");
//
//  Matrix.Multiply((mtx_type*)A, (mtx_type*)B, N, N, N, (mtx_type*)C);
//  Serial.println("\nC = A*B");
//  Matrix.Print((mtx_type*)C, N, N, "C");
//
//  // Because the library uses pointers and DIY indexing,
//  // a 1D vector can be smoothly handled as either a row or col vector
//  // depending on the dimensions we specify when calling a function
//  Matrix.Multiply((mtx_type*)C, (mtx_type*)v, N, N, 1, (mtx_type*)w);
//  Serial.println("\n C*v = w:");
//  Matrix.Print((mtx_type*)v, N, 1, "v");
//  Matrix.Print((mtx_type*)w, N, 1, "w");

 // while(1);
}

　　

依赖库文家修改

头文件

添加一个函数

int NI(mtx_type **a,   int n);

　　

/*
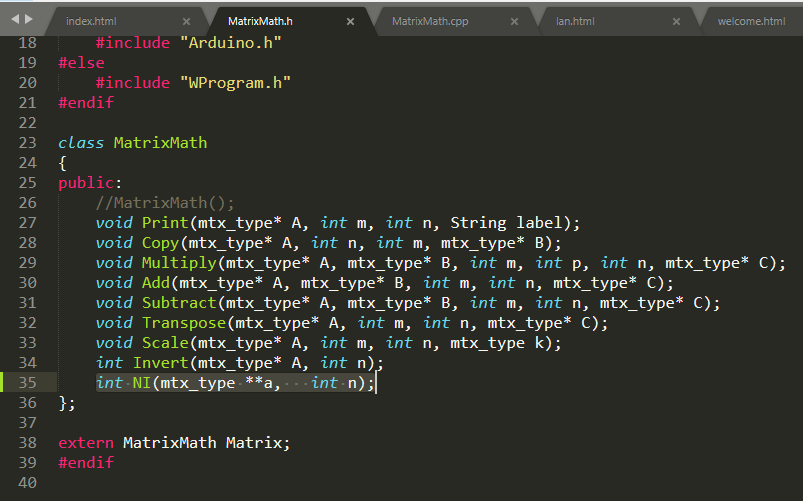
 *  MatrixMath.h Library for Matrix Math
 *
 *  Created by Charlie Matlack on 12/18/10.
 *  Modified from code by RobH45345 on Arduino Forums, algorithm from
 *  NUMERICAL RECIPES: The Art of Scientific Computing.
 *  Modified to work with Arduino 1.0/1.5 by randomvibe & robtillaart
 *  Made into a real library on GitHub by Vasilis Georgitzikis (tzikis)
 *  so that it's easy to use and install (March 2015)
 */

#ifndef MatrixMath_h
#define MatrixMath_h

#define mtx_type	float

#if defined(ARDUINO) && ARDUINO >= 100
	#include "Arduino.h"
#else
	#include "WProgram.h"
#endif

class MatrixMath
{
public:
	//MatrixMath();
	void Print(mtx_type* A, int m, int n, String label);
	void Copy(mtx_type* A, int n, int m, mtx_type* B);
	void Multiply(mtx_type* A, mtx_type* B, int m, int p, int n, mtx_type* C);
	void Add(mtx_type* A, mtx_type* B, int m, int n, mtx_type* C);
	void Subtract(mtx_type* A, mtx_type* B, int m, int n, mtx_type* C);
	void Transpose(mtx_type* A, int m, int n, mtx_type* C);
	void Scale(mtx_type* A, int m, int n, mtx_type k);
	int Invert(mtx_type* A, int n);
// 自己添加的求逆函数
	int NI(mtx_type **a,   int n);
};

extern MatrixMath Matrix;
#endif

　　库文件.cpp修改

修改后

/*
 *  MatrixMath.cpp Library for Matrix Math
 *
 *  Created by Charlie Matlack on 12/18/10.
 *  Modified from code by RobH45345 on Arduino Forums, algorithm from
 *  NUMERICAL RECIPES: The Art of Scientific Computing.
 */

#include "MatrixMath.h"

#define NR_END 1

MatrixMath Matrix;			// Pre-instantiate

// Matrix Printing Routine
// Uses tabs to separate numbers under assumption printed mtx_type width won't cause problems
void MatrixMath::Print(mtx_type* A, int m, int n, String label)
{
	// A = input matrix (m x n)
	int i, j;
	Serial.println();
	Serial.println(label);
	for (i = 0; i < m; i++)
	{
		for (j = 0; j < n; j++)
		{
			Serial.print(A[n * i + j]);
			Serial.print("\t");
		}
		Serial.println();
	}
}

void MatrixMath::Copy(mtx_type* A, int n, int m, mtx_type* B)
{
	int i, j;
	for (i = 0; i < m; i++)
		for(j = 0; j < n; j++)
		{
			B[n * i + j] = A[n * i + j];
		}
}

//Matrix Multiplication Routine
// C = A*B
void MatrixMath::Multiply(mtx_type* A, mtx_type* B, int m, int p, int n, mtx_type* C)
{
	// A = input matrix (m x p)
	// B = input matrix (p x n)
	// m = number of rows in A
	// p = number of columns in A = number of rows in B
	// n = number of columns in B
	// C = output matrix = A*B (m x n)
	int i, j, k;
	for (i = 0; i < m; i++)
		for(j = 0; j < n; j++)
		{
			C[n * i + j] = 0;
			for (k = 0; k < p; k++)
				C[n * i + j] = C[n * i + j] + A[p * i + k] * B[n * k + j];
		}
}

//Matrix Addition Routine
void MatrixMath::Add(mtx_type* A, mtx_type* B, int m, int n, mtx_type* C)
{
	// A = input matrix (m x n)
	// B = input matrix (m x n)
	// m = number of rows in A = number of rows in B
	// n = number of columns in A = number of columns in B
	// C = output matrix = A+B (m x n)
	int i, j;
	for (i = 0; i < m; i++)
		for(j = 0; j < n; j++)
			C[n * i + j] = A[n * i + j] + B[n * i + j];
}

//Matrix Subtraction Routine
void MatrixMath::Subtract(mtx_type* A, mtx_type* B, int m, int n, mtx_type* C)
{
	// A = input matrix (m x n)
	// B = input matrix (m x n)
	// m = number of rows in A = number of rows in B
	// n = number of columns in A = number of columns in B
	// C = output matrix = A-B (m x n)
	int i, j;
	for (i = 0; i < m; i++)
		for(j = 0; j < n; j++)
			C[n * i + j] = A[n * i + j] - B[n * i + j];
}

//Matrix Transpose Routine
void MatrixMath::Transpose(mtx_type* A, int m, int n, mtx_type* C)
{
	// A = input matrix (m x n)
	// m = number of rows in A
	// n = number of columns in A
	// C = output matrix = the transpose of A (n x m)
	int i, j;
	for (i = 0; i < m; i++)
		for(j = 0; j < n; j++)
			C[m * j + i] = A[n * i + j];
}

void MatrixMath::Scale(mtx_type* A, int m, int n, mtx_type k)
{
	for (int i = 0; i < m; i++)
		for (int j = 0; j < n; j++)
			A[n * i + j] = A[n * i + j] * k;
}

//Matrix Inversion Routine
// * This function inverts a matrix based on the Gauss Jordan method.
// * Specifically, it uses partial pivoting to improve numeric stability.
// * The algorithm is drawn from those presented in
//	 NUMERICAL RECIPES: The Art of Scientific Computing.
// * The function returns 1 on success, 0 on failure.
// * NOTE: The argument is ALSO the result matrix, meaning the input matrix is REPLACED
int MatrixMath::Invert(mtx_type* A, int n)
{
	// A = input matrix AND result matrix
	// n = number of rows = number of columns in A (n x n)
	int pivrow = 0;		// keeps track of current pivot row
	int k, i, j;		// k: overall index along diagonal; i: row index; j: col index
	int pivrows[n]; // keeps track of rows swaps to undo at end
	mtx_type tmp;		// used for finding max value and making column swaps

	for (k = 0; k < n; k++)
	{
		// find pivot row, the row with biggest entry in current column
		tmp = 0;
		for (i = k; i < n; i++)
		{
			if (abs(A[i * n + k]) >= tmp)	// 'Avoid using other functions inside abs()?'
			{
				tmp = abs(A[i * n + k]);
				pivrow = i;
			}
		}

		// check for singular matrix
		if (A[pivrow * n + k] == 0.0f)
		{
			Serial.println("Inversion failed due to singular matrix");
			return 0;
		}

		// Execute pivot (row swap) if needed
		if (pivrow != k)
		{
			// swap row k with pivrow
			for (j = 0; j < n; j++)
			{
				tmp = A[k * n + j];
				A[k * n + j] = A[pivrow * n + j];
				A[pivrow * n + j] = tmp;
			}
		}
		pivrows[k] = pivrow;	// record row swap (even if no swap happened)

		tmp = 1.0f / A[k * n + k];	// invert pivot element
		A[k * n + k] = 1.0f;		// This element of input matrix becomes result matrix

		// Perform row reduction (divide every element by pivot)
		for (j = 0; j < n; j++)
		{
			A[k * n + j] = A[k * n + j] * tmp;
		}

		// Now eliminate all other entries in this column
		for (i = 0; i < n; i++)
		{
			if (i != k)
			{
				tmp = A[i * n + k];
				A[i * n + k] = 0.0f; // The other place where in matrix becomes result mat
				for (j = 0; j < n; j++)
				{
					A[i * n + j] = A[i * n + j] - A[k * n + j] * tmp;
				}
			}
		}
	}

	// Done, now need to undo pivot row swaps by doing column swaps in reverse order
	for (k = n - 1; k >= 0; k--)
	{
		if (pivrows[k] != k)
		{
			for (i = 0; i < n; i++)
			{
				tmp = A[i * n + k];
				A[i * n + k] = A[i * n + pivrows[k]];
				A[i * n + pivrows[k]] = tmp;
			}
		}
	}
	return 1;
}

//自己添加的求逆函数
int MatrixMath::NI(mtx_type **a,  int n){

  int *is = new int[n];
  int *js = new int[n];
  int i,j,k;
  double d,p;
  for ( k = 0; k < n; k++)
  {
    d = 0.0;
    for (i=k; i<=n-1; i++)
      for (j=k; j<=n-1; j++)
      {
        p=fabs(a[i][j]);
        if (p>d) { d=p; is[k]=i; js[k]=j;}
      }
      if ( 0.0 == d )
      {
        free(is); free(js); Serial.println("err**not inv\n");
        return(0);
      }
      if (is[k]!=k)
        for (j=0; j<=n-1; j++)
        {
          p=a[k][j];
          a[k][j]=a[is[k]][j];
          a[is[k]][j]=p;
        }
      if (js[k]!=k)
        for (i=0; i<=n-1; i++)
        {
          p=a[i][k];
          a[i][k]=a[i][js[k]];
          a[i][js[k]]=p;
        }
      a[k][k] = 1.0/a[k][k];
      for (j=0; j<=n-1; j++)
        if (j!=k)
        {
          a[k][j] *= a[k][k];
        }
      for (i=0; i<=n-1; i++)
        if (i!=k)
          for (j=0; j<=n-1; j++)
            if (j!=k)
            {
              a[i][j] -= a[i][k]*a[k][j];
            }
      for (i=0; i<=n-1; i++)
        if (i!=k)
        {
          a[i][k] = -a[i][k]*a[k][k];
        }
  }
  for ( k = n-1; k >= 0; k--)
  {
    if (js[k]!=k)
      for (j=0; j<=n-1; j++)
      {
        p = a[k][j];
        a[k][j] = a[js[k]][j];
        a[js[k]][j]=p;
      }
      if (is[k]!=k)
        for (i=0; i<=n-1; i++)
        {
          p = a[i][k];
          a[i][k]=a[i][is[k]];
          a[i][is[k]] = p;
        }
  }
  free(is); free(js);
  return(1);

}