[CF787D] legacy

题目

Rick和他的同事们研究出了一种新的有关放射的公式，于是许多坏人就在追赶他们。所以Rick希望在被坏人抓住之前把遗产给Morty。

在他们的宇宙里总共有n颗行星，每颗行星有它自己的编号（编号为1到n）。Rick所在的行星的编号是s（地球），但是他不知道Morty在哪？总所周知，Rick有一门能打开奇妙入口的枪。在这把枪的帮助下，他能打开一扇单向门去往任意一个星球（包括那把枪自己所在的星球），但是这玩意是有限制的，因为Rick用的是这玩意的免费试用版。

一般而言，他不能用这把枪打开任意一扇单向的门。但是有q个套餐在它的官网上售卖。每一次你购买了这个套餐，你就能也仅仅能使用它一次，但是你可以重复购买（如果你觉得需要多次使用的话）。

网站上的套餐有以下三种类型：

1.打开一扇从v到u的门

2.打开一扇从v到[l,r]之间任何一个的门

3.打开一扇从[l,r]到v之间任何一个的门

Rick不知道Morty在哪？但是Unity准备告诉他。于是Rick就要准备好一切。

因为Rick的预算不多，所以他想知道从他的星球出发，到达每一个星球的最少花费是多少，如果到达不了，就输出-1.

$1<=n,q<=10^5,1<=s<=n$

题解

首先，最简单的想法就是逐条添加边，但这样的时间复杂度为$O(nm)$

注意到2,3操作的点都是连续的

所以可以考虑把这些点压成一坨一坨的

如果把它缩在线段树的节点里，那么对于一堆连续的点，最多会压成$O(logn)$个点（感性理解）

也就是说，对于2,3操作，最多只会添加$O(logn)$条边。

例如，对于操作 [2,4] - > 1,构造的图如下

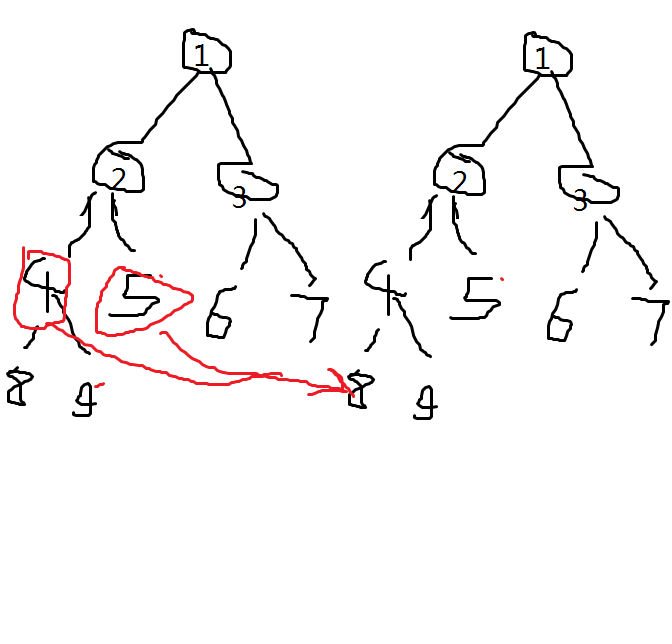
注意图中的编号是线段树节点编号。

如图，我们种两颗线段树，一棵压起点，一棵压终点

但这样我们只能走一次边，所以在原图上在稍作改造

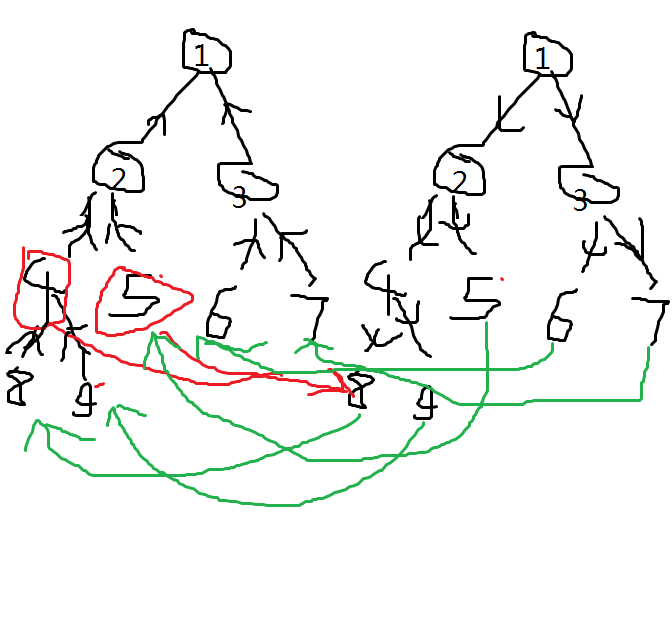
如图，我们添加了两种边

• 黑边：起点线段树子向父连接，终点线段树父向子连接
• 绿边：对应的叶子节点从终点线段树向起点线段树连接

这样，我们就可以直接在这张图上跑最短路了，

起点为s在起点线段树中的点，

记得每个点的dis要在终点树上获取

#include <iostream>
#include <cstring>
#include <cstdio>
#include <vector>
#include <queue>
#include <map>
using namespace std;
#define N 400000
#define M 1000000
#define int long long
#define mid ((l+r)>>1)
#define lc id*2,l,mid
#define rc id*2+1,mid+1,r
#define root 1,1,n
#define pr pair<int,int>
vector<pr> vec[M];
int n,cnt;
//获取[l,r]的点在线段树中压出来的点
void find(int id,int l,int r,int tl,int tr,vector<int> &area)
{
	if(l>=tl&&r<=tr)
	{
		area.push_back(id);
		return;
	}
	if(tl<=mid) find(lc,tl,tr,area);
	if(tr>mid) find(rc,tl,tr,area);
}
//获取单点在线段树中的编号
int find2(int num)
{
	vector<int> v;
	find(root,num,num,v);
	return v[0];
}
//连接[l1,r1]->[l2,r2]，即构造红边
void connect(int l1,int r1,int l2,int r2,int w)
{
	vector<int> a,b;
	find(root,l1,r1,a);
	find(root,l2,r2,b);
	cnt++;//新建一个中介节点，当然在这题没有必要
	for(int i=0;i<a.size();i++) vec[a[i]].push_back(make_pair(cnt,w));
	for(int i=0;i<b.size();i++) vec[cnt].push_back(make_pair(b[i]+N,0));
}
void build(int id,int l,int r,int num)//构造黑边
{
	if(l==r) return;
	if(!num)
	{
		vec[id*2].push_back(make_pair(id,0));
		vec[id*2+1].push_back(make_pair(id,0));
	}
	else
	{
		vec[id+N].push_back(make_pair(id*2+N,0));
		vec[id+N].push_back(make_pair(id*2+1+N,0));
	}
	build(lc,num);
	build(rc,num);
}
int s,dis[M],inq[M];
queue<int> q;
void spfa()
{
	memset(dis,0x6f,sizeof(dis));
	s=find2(s);
	dis[s+N]=dis[s]=0;
	q.push(s);
	while(!q.empty())
	{
		int now=q.front();
		q.pop();
		inq[now]=false;
		for(int i=0;i<vec[now].size();i++)
		{
			pr p=vec[now][i];
			int t=dis[now]+p.second;
			if(t<dis[p.first])
			{
				dis[p.first]=t;
				if(!inq[p.first]) q.push(p.first);
				inq[p.first]=true;
			}
		}
	}
}
signed main()
{
	//freopen("data.txt","r",stdin);
	int q;
	cin>>n>>q>>s;
	cnt=2*N;
	build(root,0);
	build(root,N);
	for(int i=1;i<=n;i++)//构造绿边
	{
		vector<int> v;
		find(root,i,i,v);
		int t=v[0];
		vec[t+N].push_back(make_pair(t,0));
	}
	for(int i=1;i<=q;i++)
	{
		int type,v,w,l,r,u;
		scanf("%lld%lld",&type,&u);
		if(type==1)
		{
			scanf("%lld%lld",&v,&w);
			connect(u,u,v,v,w);
		}
		else
		{
			scanf("%lld%lld%lld",&l,&r,&w);
			if(type==3) connect(l,r,u,u,w);
			else connect(u,u,l,r,w);
		}
	}
	spfa();
	for(int i=1;i<=n;i++)
	{
		int t=find2(i);
		if(dis[t+N]<0x7fffffffffffff) printf("%lld ", dis[t+N]);
		else printf("-1 ");
	}
}