Delaunay和Voronoi

什么是Delaunay三角剖分？

图1：Delaunay三角剖分偏爱小角度

给定平面中的一组点，三角剖分指的是将平面细分为三角形，这些点为顶点。在图1中，我们在左侧图像上看到了一组地标，在中间图像上看到了三角剖分。一组点可以有许多可能的三角剖分，但是Delaunay三角剖分之所以突出是因为它具有一些不错的特性。在Delaunay三角剖分中，选择三角形时应确保没有点位于任何三角形的外接圆之内。图2.显示了四个点A，B，C和D的Delaunay三角剖分。在顶部图像中，要使该三角剖分成为有效的Delaunay三角剖分，C点应在三角形ABD外接圆的外部，而A点应在三角形ABD的外接圆的外部三角形BCD的外接圆。

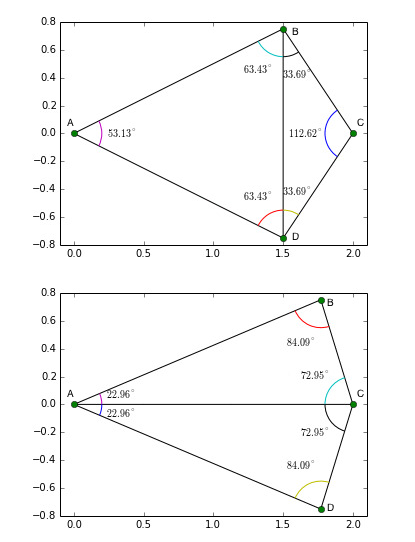
Delaunay三角剖分的一个有趣特性是它不支持“瘦”三角形（即，一个大角度的三角形），即选择小角三角形，如下：

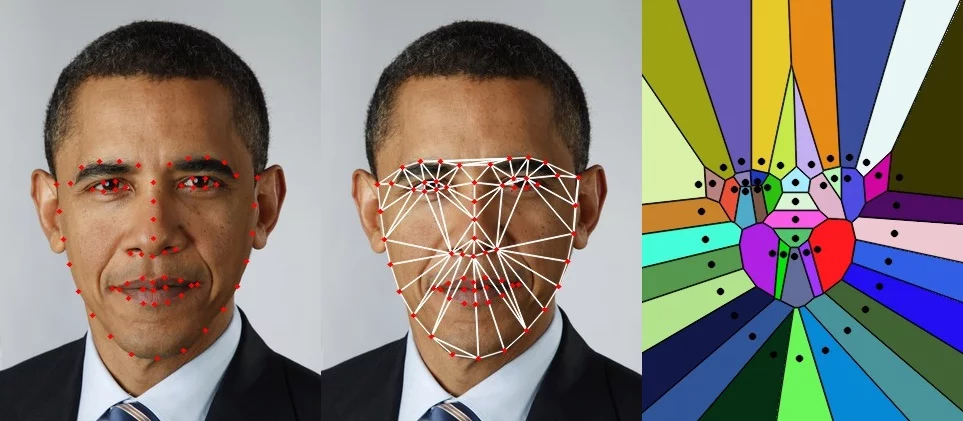
图1显示了在移动点时三角剖分如何变化以拾取“胖”三角形。在顶部图像中，点B和D在x = 1.5处具有x坐标，在底部图像中，它们向右移至x = 1.75。在顶部图像角度中，ABC和ABD的角度较大，而Delaunay三角剖分在B和D之间创建了一条边缘，将两个大角度分为较小的角度ABD，ADB，CDB和CBD。另一方面，在底部图像中，角度BCD太大，并且Delaunay三角剖分创建了边缘AC以划分大角度。

有很多算法可以找到一组点的Delaunay三角剖分。最明显（但不是最有效）的方法是从任何三角剖分开始，然后检查任何三角形的外接圆是否包含另一个点。如果是这样，则翻转边缘（如图1所示）并继续直到没有外接圆包含点的三角形。

关于Delaunay三角剖分的任何讨论都必须包括Voronoi图，因为一组点的Voronoi图是其Delaunay三角剖分的数学对偶。

什么是Voronoi图？

图2. Voronoi图

给定平面中的一组点，Voronoi图会划分空间，以使边界线与相邻点等距。图2.显示了根据显示为黑点的点计算的Voronoi图的示例。您会注意到，每条边界线都经过两个点的中心。如果将相邻的Voronoi地区中的点连接起来，则会得到Delaunay三角剖分！

Delaunay三角剖分和Voronoi图之间的联系不止一种。