Aladdin and the Flying Carpet LightOJ 1341 唯一分解定理

题意:给出a,b，问有多少种长方形满足面积为a,最短边>=b？

首先简单讲一下唯一分解定理。

唯一分解定理：任何一个自然数N，都可以满足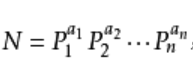：，pi是质数。

且N的正因子个数为(1+a1)*(1+a2)*(1+a3)*.......*(1+an)。

看了网络上很多人写的题解，普遍的做法是先找出N的所有正因子n，(n/2)就是在不考虑最短边>=b时所有存在的长方形，现在考虑最短边>=b，只需要减去所有能整除a且小于b的因子即可。

具体写法：

1.先预处理素数

2.用唯一分解定理求出N的所有因子

3.减去使得最短边<b的因子对

AC code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
bool u[];
ll su[];
ll a,b,tmp,num,sum;
void olas()
{
    num=;
    memset(u,true,sizeof(u));
    for(ll i=; i<=; i++)
    {
        if(u[i])    su[num++]=i;
        for(ll j=; j<num; j++)
        {
            if(i*su[j]>)    break;
            u[i*su[j]]=false;
            if(i%su[j]==)    break;
        }
    }
}
void cal()
{
    sum=;
    for(ll i=; i<num&&su[i]<=sqrt(tmp); i++)
    {
        ll cc=;
        while(tmp%su[i]==)
        {
            cc++;
            tmp/=su[i];
        }
        sum*=(+cc);
    }
    if(tmp>)    sum*=;
}
int main()
{
    //freopen("input.txt","r",stdin);
    olas();
    ll T,kase=;
    scanf("%lld",&T);
    while(T--)
    {
        scanf("%lld%lld",&a,&b);
        if(a<b*b)    printf("Case %lld: 0\n",kase++);
        else
        {
            tmp=a;
            cal();
            sum/=;
            for(ll i=; i<b; i++)
            {
                if(a%i==)    sum--;
            }
            printf("Case %lld: %lld\n",kase++,sum);
        }
    }
    return ;
}

存疑：

虽然说按照以上写法可以AC，考虑到有T可以取到4000，b可以取到1000000，假设有测试数据如下：

T = 4000

case 1:a=10^12 ,b=10^6

case 2:a=10^12 ,b=10^6-1

case 3:a=10^12 ,b=10^6-2

.......

case 4000:a=10^12,b=10^6-3999

这样一来由于每次都遍历了1->b，真实时间复杂度>O(4000*10^6)在3000ms内必然TLE。

但是本题不存在这样的测试数据。。。。。。。所以可以直接水过。。