Topoi 测验1301, 问题C: 1959: 解题 解题报告

Topoi（一个经常会炸的网站）

本题提交链接

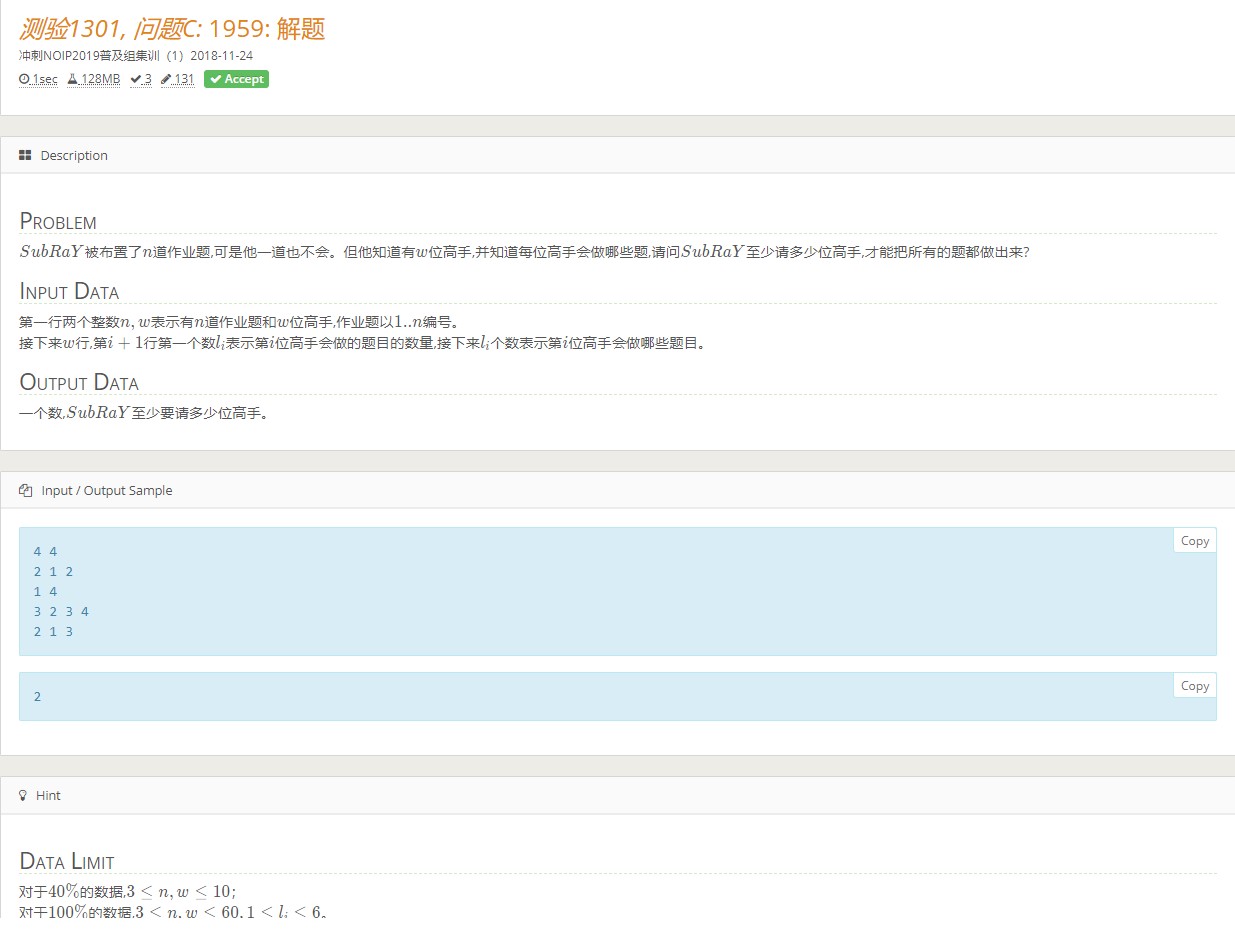
很久以前的题目了， 刚开了博客，来写一波题解

先看一波提交记录：

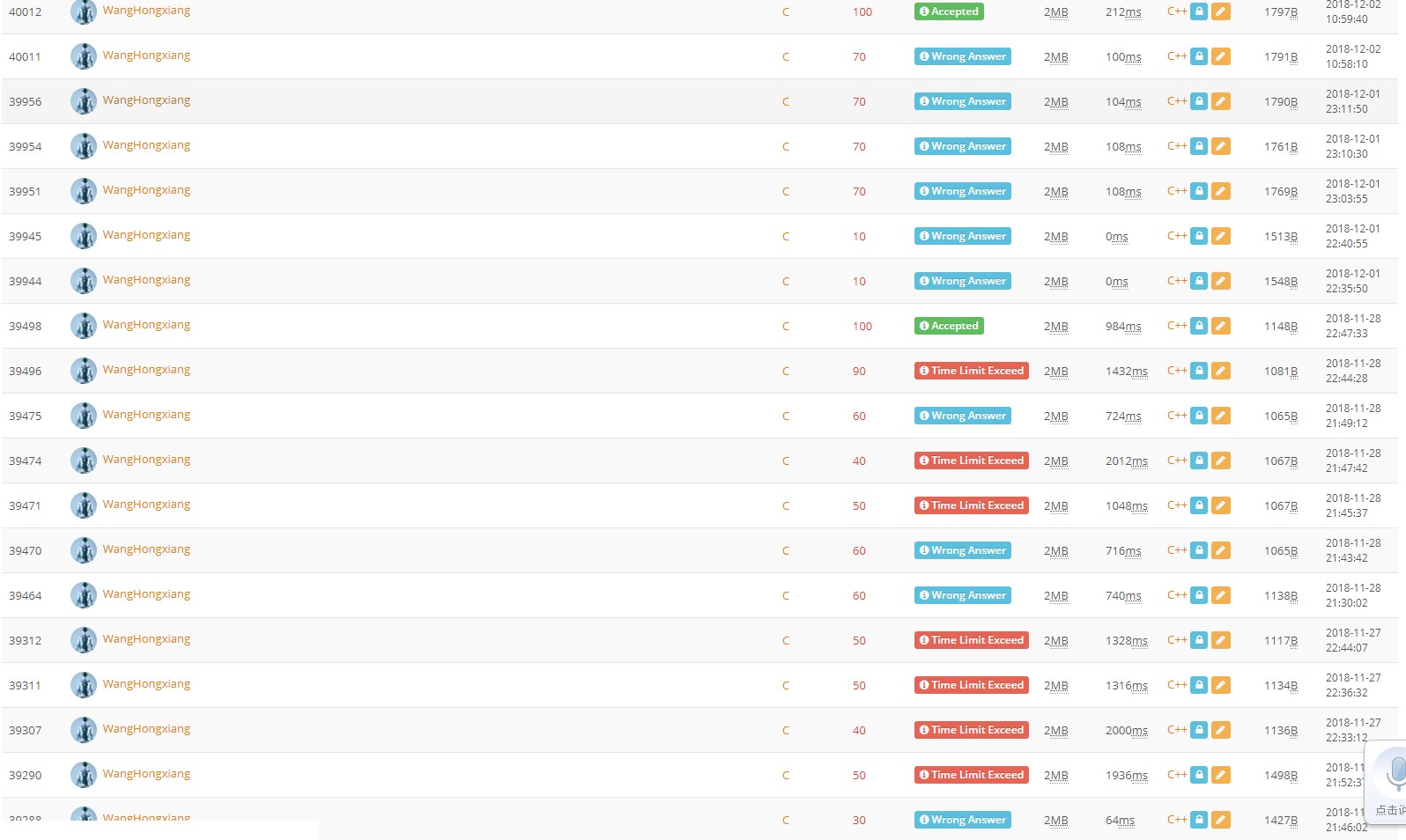
调了好几天QAQ

唉！ 要是这些高手里有我估计直接 输出1 就AC了

算法

DFS + 优化剪枝（用了一点状态压缩）

剪枝

1：求最小值很容易向导最优化剪枝

if(ws>=ans) return;  //剪枝 1：最优化剪枝 

2：若一个高手会做的题有另一个高手都会做，则这个高手没有用

for(int i=1;i<=w;i++)
      for(int j=1;j<i;j++)
      {;
          if((a[i].sn|a[j].sn)==a[j].sn) {kk[i]=1; break;} //kk表示这个高手有没有用
    //剪枝 2：若这个高手会做的题有另一个人全会做，则是废物，去掉没有用的高手 （核心剪枝）
      }

3：若有一个题只有一个高手能做，则将这个高手“特招”

for(int i=1;i<=w;i++)
      for(int j=1;j<i;j++)
      {;
          if((a[i].sn|a[j].sn)==a[j].sn) {kk[i]=1; break;} //kk表示这个高手有没有用
    //剪枝 2：若这个高手会做的题有另一个人全会做，则是废物，去掉没有用的高手 （核心剪枝）
      }

顺序性优化：将做题多的高手排在前面（也许没用）

bool cmp(node x,node y){return x.sum>y.sum;}
sort(a+1,a+n+1,cmp);  //顺序性优化： 按会做的题数排序

加上这些优化在top上大概200多ms（第二次AC记录），应该还有其他优化，但因为太ruo想不出来

这题用二进制表示状态好像多此一举

最后，附上完整代码（有点小长）

打注释都打了半个多小时QAQ

代码

#include <bits/stdc++.h>
using namespace std;
int n,w,ans=1e9,tt;//tt记录特招人数
bool k[66],kk[66],vis[66]; //k记录是否“特招”，kk记录有木有用，vis标记访问
struct node{
	long long sn,sum;
	int p[66];
}a[66]; //p数组记录每个高手能做的题，sn记录状态，sum记录题数，
long long num[66],q[66][66],s[66],ss[66];
//q记录每个题能做的高手，s和ss记录每个题能做的人数（有点重复了），num记录每个题的二进制，
bool cmp(node x,node y){return x.sum>y.sum;}
void find(int x,int ws,long long ssum)  //x表示当前题号， ws表示高手数， ssum用二进制存储状态
{
    if(ws>=ans) return;  //剪枝 1：最优化剪枝
    if(x>n) {ans=ws; return;} //结束条件， 更新答案
    if(((ssum>>(x-1))&1==1)) {find(x+1,ws,ssum); return;} //如果这题已做，往后搜索
    for(int i=1;i<=s[x];i++)
    {
    	if(k[q[x][i]]) continue; //判断这个高手是不是 “特招”的
    	int tmp=q[x][i];
    	if(vis[tmp]) continue; //如果这个高手已经用过了
    	vis[tmp]=1;
    	find(x+1,ws+1,ssum|a[tmp].sn); //一定要用 | 运算，防止重复
    	vis[tmp]=0;
	}
	return;
}
int main()
{
    scanf("%d%d",&n,&w);
    num[1]=1;
    for(int i=2;i<=n;i++) num[i]=num[i-1]<<1; //用2进制来表示状态
    for(int i=1;i<=w;i++)
    {
        int x;
        scanf("%d",&x);
        for(int j=1;j<=x;j++)
        {
            int y;
            scanf("%d",&y);
            s[y]++;
            if((a[i].sn|num[y])!=a[i].sn)   //注意这里要用 | 运算，判断这题有没有出现过
			  a[i].sum++,a[i].p[a[i].sum]=y;  //存储每个高手能做的题
            a[i].sn=a[i].sn|num[y];   //更新状态
        }
    }
    sort(a+1,a+n+1,cmp);  //顺序性优化： 按会做的题数排序
    for(int i=1;i<=w;i++)
      for(int j=1;j<i;j++)
      {
    //  	if(i==j||kk[j]) continue;
      	if((a[i].sn|a[j].sn)==a[j].sn) {kk[i]=1; break;} //kk表示这个高手有没有用
    //剪枝 2：若这个高手会做的题有另一个人全会做，则是废物，去掉没有用的高手 （核心剪枝）
	  }
	long long ttmp=0;
	for(int i=1;i<=w;i++)
	{
		if(kk[i]) continue;  //直接过滤废物高手
	    for(int j=1;j<=a[i].sum;j++)
	    {
	    	int tmp=a[i].p[j];
	  	    q[tmp][++ss[tmp]]=i;
	    }
	}
    //记录能做每个题的高手
	for(int i=1;i<=n;i++)
	{
		if(s[i]==1&&!k[q[i][1]]) //判断第i题是不是只有一个高手会做
		{
		  tt++;
		  //printf("%d\n",q[i][1]);
		  int tmp=q[i][1];
		  ttmp=ttmp|a[tmp].sn;  //ttmp记录初始的搜索状态
		  k[tmp]=1;  //标记这个高手不用考虑
		}
	} //剪枝 3：若有一个题只有一个高手会做，将他“特招”进来 （这个剪枝收益蛮大的）
	find(1,0,ttmp);
    printf("%d",ans+tt); //注意不要忘了加上“特招”人数
    return 0;
}