Reproducing kernel Hilbert space Mapping the points to a higher dimensional feature space

http://www.gatsby.ucl.ac.uk/~gretton/coursefiles/lecture4_introToRKHS.pdf

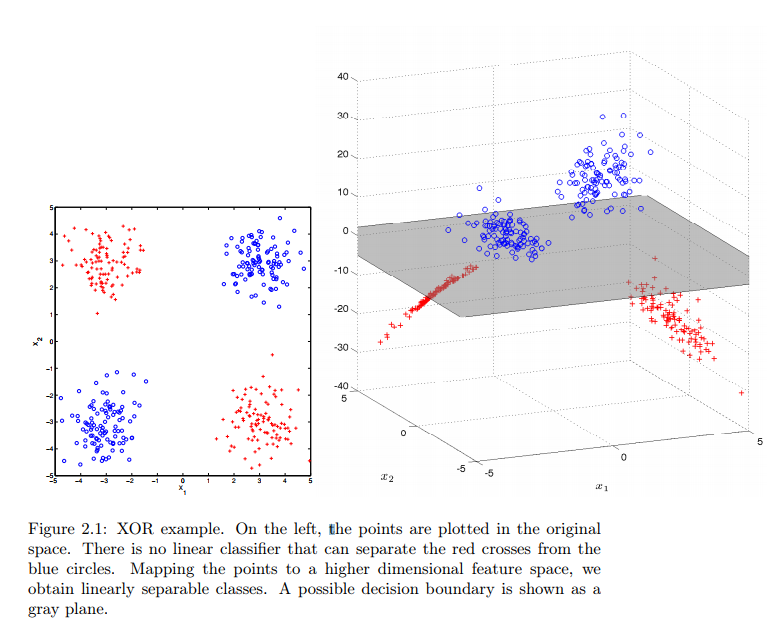
【We next show that every reproducing kernel Hilbert space has a unique positive definite kernel, and vice-versa: this is the Moore-Aronszajn theorem.】

每个可繁殖核希尔伯特空间有一个唯一的正定的核。

Every positive definite kernel k is associated with a unique RKHS H.

We have introduced the notation of feature spaces, and kernels on these feature spaces. What’s more, we’ve determined that these kernels are positive definite. In this section, we use these kernels to define functions on X . The space of such functions is known as a reproducing kernel Hilbert space.

【函数空间-RKHS】

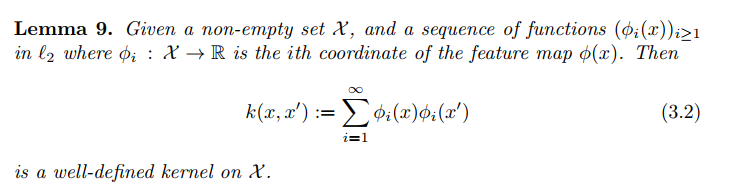
The space of such functions is known as a reproducing kernel Hilbert space.的更多相关文章

  1. paper 10：支持向量机系列七：Kernel II —— 核方法的一些理论补充，关于 Reproducing Kernel Hilbert Space 和 Representer Theorem 的简介。

    在之前我们介绍了如何用 Kernel 方法来将线性 SVM 进行推广以使其能够处理非线性的情况,那里用到的方法就是通过一个非线性映射 ϕ(⋅) 将原始数据进行映射,使得原来的非线性问题在映射之后的空间 ...

  2. Reproducing Kernel Hilbert Space (RKHS)

    目录 概 主要内容 RKHS-wiki 概 这里对RKHS做一个简单的整理, 之前的理解错得有点离谱了. 主要内容 首先要说明的是, RKHS也是指一种Hilbert空间, 只是其有特殊的性质. Hi ...

  3. Cauchy sequence Hilbert space 希尔波特空间的柯西序列

    http://mathworld.wolfram.com/HilbertSpace.html A Hilbert space is a vector space  with an inner prod ...

  4. Hilbert space

    Definition A Hilbert space H is a real or complex inner product space that is also a complete metric ...

  5. 希尔伯特空间（Hilbert Space）是什么？

    希尔伯特空间是老希在解决无穷维线性方程组时提出的概念, 原来的线性代数理论都是基于有限维欧几里得空间的, 无法适用, 这迫使老希去思考无穷维欧几里得空间, 也就是无穷序列空间的性质. 大家知道, 在一 ...

  6. 希尔伯特空间（Hilbert Space）

    欧氏空间 → 线性空间 + 内积 ⇒ 内积空间(元素的长度,元素的夹角和正交) 内积空间 + 完备性 ⇒ 希尔伯特空间 0. 欧几里得空间 欧氏空间是一个特别的度量空间,它使得我们能够对其的拓扑性质, ...

  7. Are Loss Functions All the Same?

    目录 概 主要内容 一些假设 损失函数 损失函数的统计性质 收敛速度 分类的界 Rosasco L, De Vito E, Caponnetto A, et al. Are loss function ...

  8. Kernel methods on spike train space for neuroscience: a tutorial

    郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布! 时序点过程:http://www.tensorinfinity.com/paper_154.html Abstract 在过去的十年中,人 ...

  9. Deep Learning and Shallow Learning

    Deep Learning and Shallow Learning 由于 Deep Learning 现在如火如荼的势头,在各种领域逐渐占据 state-of-the-art 的地位,上个学期在一门 ...

随机推荐

  1. Scala和Java二种方式实战Spark Streaming开发

    一.Java方式开发 1.开发前准备:假定您以搭建好了Spark集群. 2.开发环境采用eclipse maven工程,需要添加Spark Streaming依赖. 3.Spark streaming ...

  2. [PWA] Access the Camera in a PWA built with React

    It's possible to access some, but not all, of the native device features from a PWA. One that we can ...

  3. Android Tabhost置于底部

    方法一: <TabHost xmlns:android="http://schemas.android.com/apk/res/android" android:id=&qu ...

  4. 使用SQLite存储数据

    一.SQLiteAndroid 为了让我们能够更加方便地管理数据库, 专门提供了一个SQLiteOpenHelper 帮助类,借助这个类就可以非常简单地对数据库进行创建和升级. 1.SQLiteOpe ...

  5. foreach和volist的区别

      foreach和volist的区别   1.foreach标签foreach标签用于循环输出:foreach(name,item,key)name(必须):要输出的数据模板变量item(必须):循 ...

  6. Business Process and SAP ERP

    1. Definition of Organisation - Organizations are created entities within and through which people i ...

  7. bios文字解释

    很多笔记本电脑用户由于不熟悉bios,导致在需要设置bios时不知如何下手,其实bios基本大同小异,熟悉了以后再遇到bios设置就手到擒来了. 今天我们以笔记本电脑为例,进行bios界面的解读. 1 ...

  8. PHP面试题及答案解析(6)—PHP网络编程

    1.禁用COOKIE后SEESION还能用吗? 可以,COOKIE和SESSION都是用来实现会话机制的,由于http协议是无状态的,所以要想跟踪一个用户在同一个网站之间不同页面的状态,需要有这么一个 ...

  9. PHP面试题及答案解析(1)—PHP语法基础

    1. strlen( )与 mb_strlen( )的作用分别是什么? strlen和mb_strlen都是用于获取字符串长度.strlen只针对单字节编码字符,也就是说它计算的是字符串的总字节数.如 ...

  10. 【HttpClient4.5中文教程】【第一章 ：基础】1.1运行请求（二）

    很多其它HttpClient4.5中文教程请查看:点击打开链接 ==================================================================== ...