EM最大期望算法

【简介】

　　em算法，指的是最大期望算法（Expectation Maximization Algorithm，又译期望最大化算法），是一种迭代算法，在统计学中被用于寻找，依赖于不可观察的隐性变量的概率模型中，参数的最大似然估计。

　　EM 算法是 Dempster,Laind,Rubin 于 1977 年提出的求参数极大似然估计的一种方法，它可以从非完整数据集中对参数进行 MLE 估计，是一种非常简单实用的学习算法。这种方法可以广泛地应用于处理缺损数据，截尾数据，带有噪声等所谓的不完全数据。可以有一些比较形象的比喻说法把这个算法讲清楚。比如说食堂的大师傅炒了一份菜，要等分成两份给两个人吃，显然没有必要拿来天平一点的精确的去称分量，最简单的办法是先随意的把菜分到两个碗中，然后观察是否一样多，把比较多的那一份取出一点放到另一个碗中，这个过程一直迭代地执行下去，直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。

　　EM算法就是这样，假设我们估计知道A和B两个参数，在开始状态下二者都是未知的，并且知道了A的信息就可以得到B的信息，反过来知道了B也就得到了A。可以考虑首先赋予A某种初值，以此得到B的估计值，然后从B的当前值出发，重新估计A的取值，这个过程一直持续到收敛为止（百度百科）。

【算法】

　　1、计算期望（E），利用概率模型参数的现有估计值，计算隐藏变量的期望；

　　2、最大化（M），利用E 步上求得的隐藏变量的期望，对参数模型进行最大似然估计；

　　3、M 步上找到的参数估计值被用于下一个 E 步计算中，这个过程不断交替进行。

【代码】

　　

import math;
import copy;
import numpy as np;
import matplotlib.pyplot as plt;

isdebug = True  

# 指定k个高斯分布參数。这里指定k=2。注意2个高斯分布具有同样均方差Sigma，分别为M1,M2。
def getdataSet(Sigma,M1,M2,k,N):
    #创建长度为N的数据
    dataSet = np.zeros((1,N))
    for i in range(N):
        #为数据赋值，并随机分开两组数据
        if np.random.random(1) > 0.333:
            dataSet[0,i] = np.random.normal()*Sigma + M1
        else:
            dataSet[0,i] = np.random.normal()*Sigma + M2
    if isdebug:
        print ("dataSet:",dataSet)
    return dataSet  

# E算法：计算期望E[zij]
def E(Sigma,dataSet,Miu,k,N):
    #创建概率数组
    Exp = np.zeros((N,k))
    Num = np.zeros(k)
    for i in range(N):
        Sum = 0
        for j in range(k):
            #求数据的高斯分布概率
            Num[j] = math.exp((-1/(2*(float(Sigma**2))))*(float(dataSet[0,i]-Miu[j]))**2)
            Sum += Num[j]
        for j in range(k):
            #求没类数据在各类中的占比，即隐藏变量Z
            Exp[i,j] = Num[j] / Sum
    if isdebug:
        print ("Exp:",Exp)  

    return Exp  

# M算法：最大化E[zij]的參数Miu
def M(Exp,dataSet,k,N):
    Miu = np.random.random(k)
    for j in range(k):
        Num = 0
        Sum = 0
        for i in range(N):
            Num += Exp[i,j]*dataSet[0,i]
            Sum += Exp[i,j]
        Miu[j] = Num / Sum
        if isdebug:
            print("Miu:",Miu)
    return Miu  

#初始参数
Sigma = 6
M1 = -20
M2 = 20
k=2
N=0xffff #65535
Iter=0xff
EPS =1e-6  

#随机初始数据
dataSet=getdataSet(Sigma,M1,M2,k,N)  

#初始先假设一个E[zij]
Miu = np.random.random(2)
# 算法迭代
for i in range(Iter):
    oldMiu = copy.deepcopy(Miu)
    #E
    Exp = E(Sigma,dataSet,Miu,k,N)
    #M
    Miu = M(Exp,dataSet,k,N)
    #如果达到精度Epsilon停止迭代
    if sum(abs(Miu-oldMiu)) < EPS:
       if isdebug:
            print ("Iter:",i)
       break  

plt.figure('emmmmm',figsize=(12, 6))
plt.hist(dataSet[0,:],100)
plt.xticks(fontsize=10, color="darkorange")
plt.yticks(fontsize=10, color="darkorange")
plt.show()

【结果】

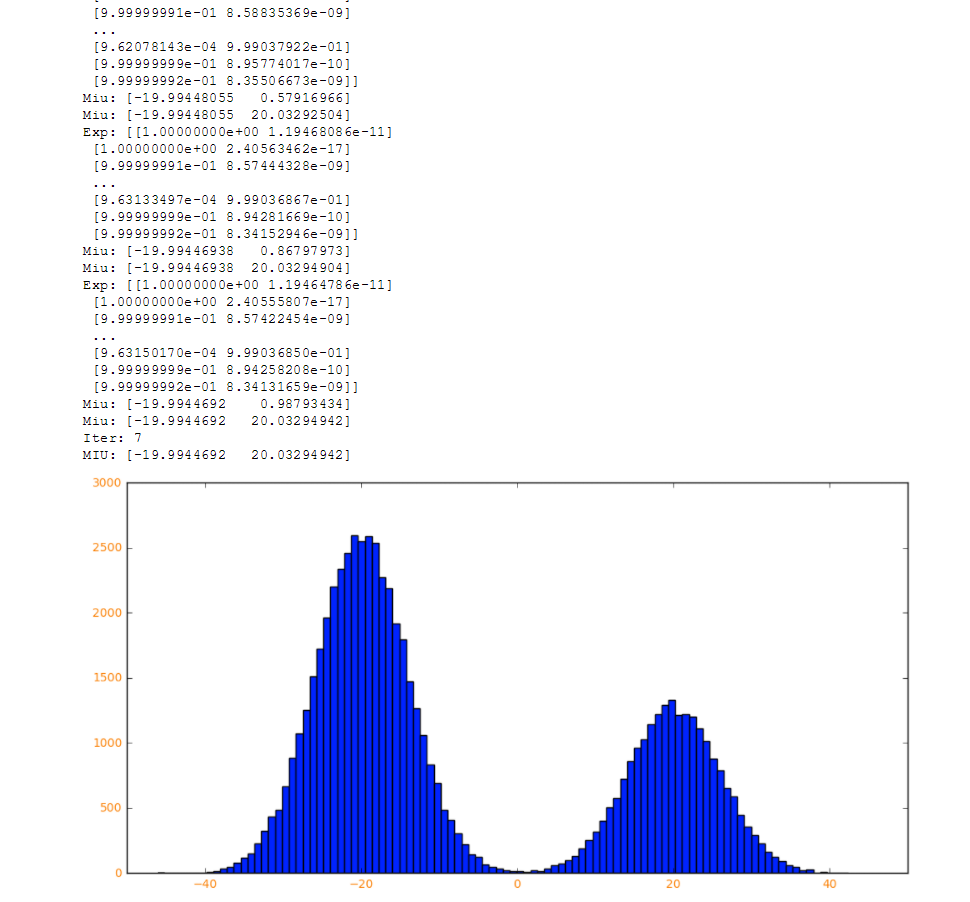
【参考文献】

https://blog.csdn.net/sm9sun/article/details/78745265

https://www.cnblogs.com/cxchanpin/p/6731780.html

------------------------------------------华丽的分割线------------------------------------------------------

有兴趣的同学可以关注公总号：RaoRao1994