[AGC008E] Next or Nextnext [环套树森林+结论讨论]

题面

传送门

思路

p到a

首先，本题中如果对于所有的$i$，连边$<i,p_i>$，那么可以得到一批环

那么这个题另外一点就是，可以变成连边$<i,p_{p_i}>$

我们分多种情况来讨论

情况1：啥也没变

就是啥也没变

情况2：全都变了

这时考虑奇环和偶环

对于一个奇环，全部变了以后，它还是一个环，但是不是同构的

对于一个偶环，全换了以后，它会变成两个环，分别是全部奇数节点和全部偶数节点

情况3：变了一部分

此时容易发现，变出去的部分应该会这样：

$<i,p_i>$变成$<i,p_{p_i}>$，则$p_i$变成环上外挂的一个节点

这样一直讨论下去可以得到，最终我们会得到一棵环套树，并且每一棵树都只有可能是一条链

对于每一条链我们这样考虑：

如果链形如这样：

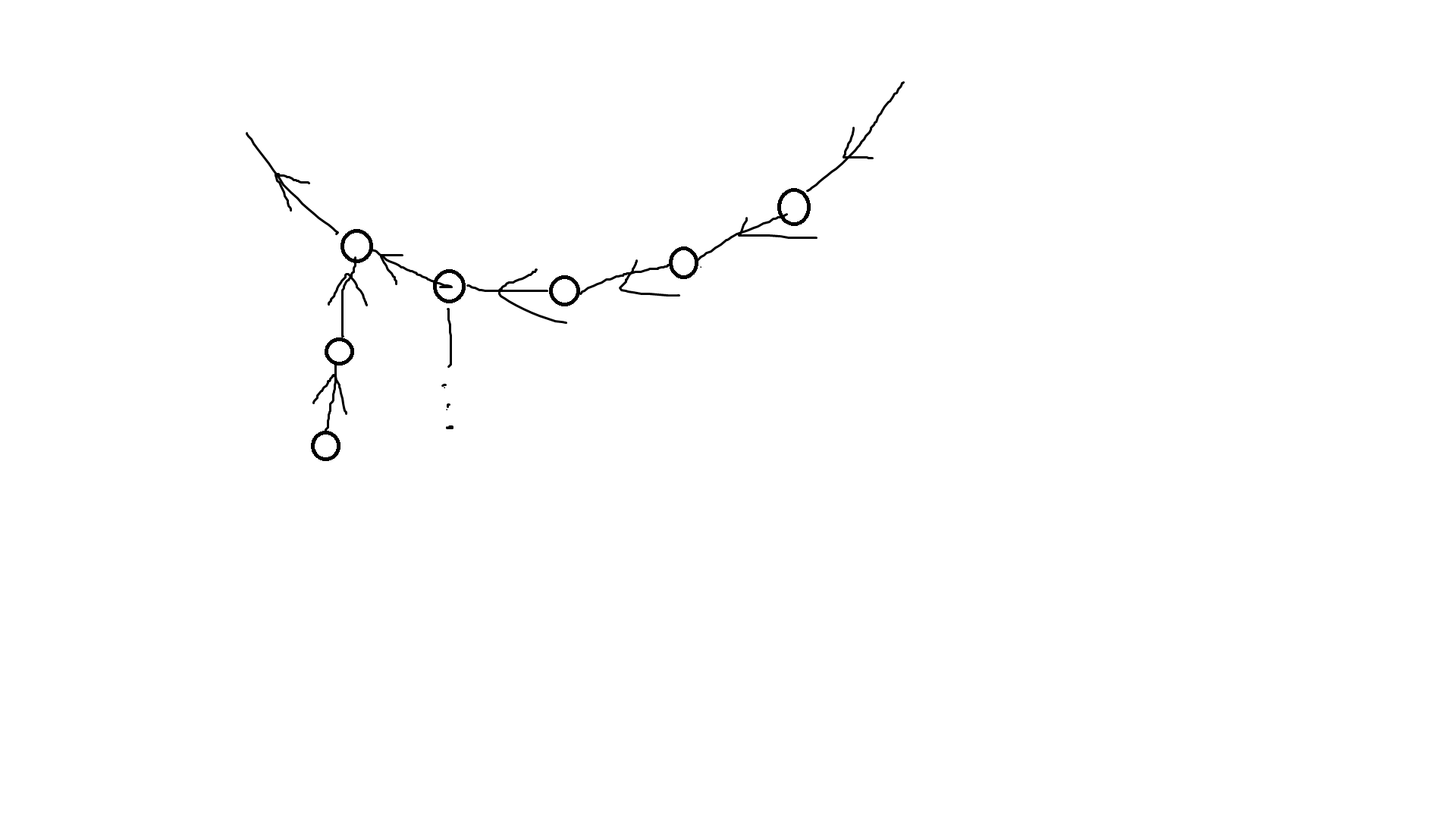
那么肯定ans=0，因为这个长度为2的链没有2条环边配合它

如果是这样：

如果恰好相等，那么这条链只有一种情况

如果不相等，那么这条链会有两种情况：放在这一段环的最开始和最末尾

此时它对答案贡献一个乘2

a到p

讨论完以后，我们回到问题本身，发现我们拿到了的是$a$不是$p$

所以我们要求的实际上就是这个$<i,a_i>$图反推回去的方案数

那么，我们把环和环套树分开处理

显然环套树就是按照上面的讨论，乘1乘2或者乘0

对于所有长度相同的环，我们需要考虑它们两两合并的情况

此时可以用数学方法很快求出

具体一点来说，如果有$n$个长度为$L$的环，那么它们的贡献就是

$\sum_{t=0}^{\lfloor \frac{n}{2}\rfloor} L^n f(t2) C(n,2t) $

如果$n$是大于1的奇数还要再乘以2（因为此时可以像上面说的那样自我同构一下）

其中$f(2t)$表示的是$2t$个数互相配对的方案数

最后把所有长度的环的贡献乘起来，再乘上每个环套树的贡献，就是答案了

Code

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#define ll long long
#define MOD 1000000007
using namespace std;
inline int read(){
	int re=0,flag=1;char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-') flag=-1;
		ch=getchar();
	}
	while(isdigit(ch)) re=(re<<1)+(re<<3)+ch-'0',ch=getchar();
	return re*flag;
}
ll f[200010],finv[200010],meth[200010];
ll qpow(ll a,ll b){
	ll re=1;
	while(b){
		if(b&1) re=(re*a)%MOD;
		a=a*a%MOD;b>>=1;
	}
	return re;
}
void init(){
	ll i,len=200000;
	f[0]=f[1]=finv[0]=finv[1]=1;
	for(i=2;i<=len;i++) f[i]=f[i-1]*i%MOD;
	finv[len]=qpow(f[len],MOD-2);
	for(i=len;i>2;i--) finv[i-1]=finv[i]*i%MOD;
}
int n,a[200010],vis[200010],cir[200010],cntcir=0,in[200010],bst[200010],siz[200010];
ll ans=1;
vector<int>s;
vector<int>nd[200010];
bool cmp(int l,int r){
	return siz[l]<siz[r];
}
ll C(ll x,ll y){
	return f[x]*finv[y]%MOD*finv[x-y]%MOD;
}
int main(){
	n=read();int i,j;ll tmp,c,cc;
	init();
	meth[0]=1;
	for(i=1;i<=n;i++) meth[i]=C(i*2,i)*f[i]%MOD*qpow(qpow(2,MOD-2),i)%MOD;

	for(i=1;i<=n;i++) a[i]=read(),in[a[i]]++;
	for(i=1;i<=n;i++){//取出环
		j=i;
		while(!vis[j]) vis[j]=i,j=a[j];
		if(vis[j]^i) continue;
		cntcir++;
		while(!cir[j]){
			cir[j]=cntcir,nd[cntcir].push_back(j),siz[cntcir]++,j=a[j];
		}
	}
	memset(vis,0,sizeof(vis));
	for(i=1;i<=n;i++){//判断环套树，以及外挂树是不是都是链
		if(in[i]) continue;
		j=i;
		while(!cir[j]&&!vis[j]) j=a[j];
		if(vis[j]){
			puts("0");return 0;
		}
		bst[cir[j]]=1;tmp=cir[j];
		j=i;c=0;
		while(!cir[j]) cir[j]=tmp,c++,vis[j]=1,j=a[j];
		vis[j]=c;
	}
	for(i=1;i<=cntcir;i++){//环套树处理
		if(!bst[i]){s.push_back(i);continue;}
		for(j=0;j<nd[i].size();j++) if(vis[nd[i][j]]) break;
		tmp=j;
		do{
			c=j;cc=1;
			j--;
			(j+=(int)nd[i].size());
			j%=(int)nd[i].size();
			for(;!vis[nd[i][j]];j--,j=((j<0)?j+nd[i].size():j)) cc++;
			if(vis[nd[i][c]]>cc){
				puts("0");return 0;
			}
			if(vis[nd[i][c]]<cc) (ans*=2)%=MOD;
		}while(tmp!=j);
	}
	sort(s.begin(),s.end(),cmp);
	for(i=0;i<s.size();i+=c){
		j=i;tmp=0;
		while(siz[s[j]]==siz[s[i]]&&j<s.size()) j++;
		c=j-i;
		for(j=0;j<=c/2;j++){
			(tmp+=C(c,2*j)*meth[j]%MOD*qpow(siz[s[i]],j)%MOD*qpow(2,(c-2*j)*(siz[s[i]]!=1)*(siz[s[i]]&1))%MOD)%=MOD;
		}
		ans=ans*tmp%MOD;
	}
	printf("%lld\n",ans);
}