形式化验证工具（PAT）Reader-Writers Problem学习

经过前几次的学习，我们应该对PAT有一点点的了解了，我们加下来就直接看例子中的一个问题，这个问题比较简单。

看代码：

//The classic Readers/Writers Example model multiple processes accessing a shared file.

////////////////The Model//////////////////
//the maximun size of the readers that can read concurrently
#define M 2;
var writing = false;
var noOfReading = ;

Writer()     = [noOfReading ==  && !writing]startwrite{writing = true;} -> stopwrite{writing = false;} -> Writer();
Reader()     = [noOfReading < M && !writing]startread{noOfReading = noOfReading+;} ->
                          //the following guard condition is important to avoid infinite state space, because noOfReading can go negtively infinitely
                          ([noOfReading > ]stopread{noOfReading = noOfReading-;} -> Reader());

//there are infinite number of Readers and Writers
ReadersWriters() = |||{..} @ (Reader() ||| Writer());

////////////////The Properties//////////////////
#assert ReadersWriters() deadlockfree;
#define exclusive !(writing == true && noOfReading > 0);
#assert ReadersWriters() |= [] exclusive;
#define someonereading noOfReading > 0;
#assert ReadersWriters() |= []<>someonereading;
#define someonewriting writing == true;
#assert ReadersWriters() |= []<>someonewriting;

首先定义了一个M，这个M表示可以同时读书的最大读者数量。接下来定义了一个变量writing，表示是否在写。然后定义了noOfReading,表示在阅读的读者数量。

接下来我们看两个行为，写行为：

Writer()     = [noOfReading ==  && !writing]startwrite{writing = true;} -> stopwrite{writing = false;} -> Writer();

写行为有一个前置gurd条件，就是在读书的人数必须是0而且不能有在写的，然后这个行为才可以写，写的时候把writing置为true，然后是停止写（writing置为false），然后回到写行为。

读行为：

Reader()     = [noOfReading < M && !writing]startread{noOfReading = noOfReading+;} ->
                          //the following guard condition is important to avoid infinite state space, because noOfReading can go negtively infinitely
                          ([noOfReading > ]stopread{noOfReading = noOfReading-;} -> Reader());

同样的，读行为也有一个前置条件，就是在读书的人数必须小于M，而且不能有在写的，然后这个行为才可以阅读（阅读人数加一），然后在阅读人数大余0的情况下，才可以停止阅读（阅读人数减一），然后回到阅读行为。

然后就是整个系统：

ReadersWriters() = |||{..} @ (Reader() ||| Writer());

我们看到前两种行为是没有交集的，所以，这里使用的三个竖线，就是interleaving。然后可以有无穷多的读者和作者过来。

下面就是一些验证了。

首先看看是不是不会发生死锁？我们自己来分析分析，系统肯定不会发生死锁，因为两个行为没有交集，都是一步一步运行下去。但是当我们验证的时候看到如下的结果。

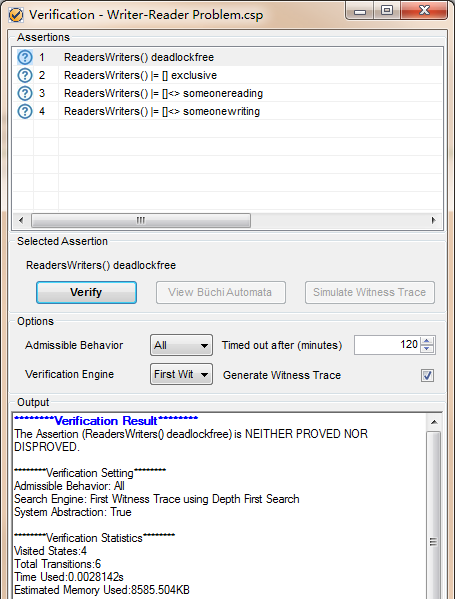
结果表示PAT验证这个命题是正确还是错误，这是为什么呢？仔细的读者肯定能想到，我们的系统里面有无数个人过来，PAT根本走不到最后一个节点，甚至根本走不完所有的节点。所以PAT给一个结果表示无法验证（

NEITHER PROVED NOR DISPROVED），这里如果我们修改过来的人数，就可以看到验证结果是没有问题的。

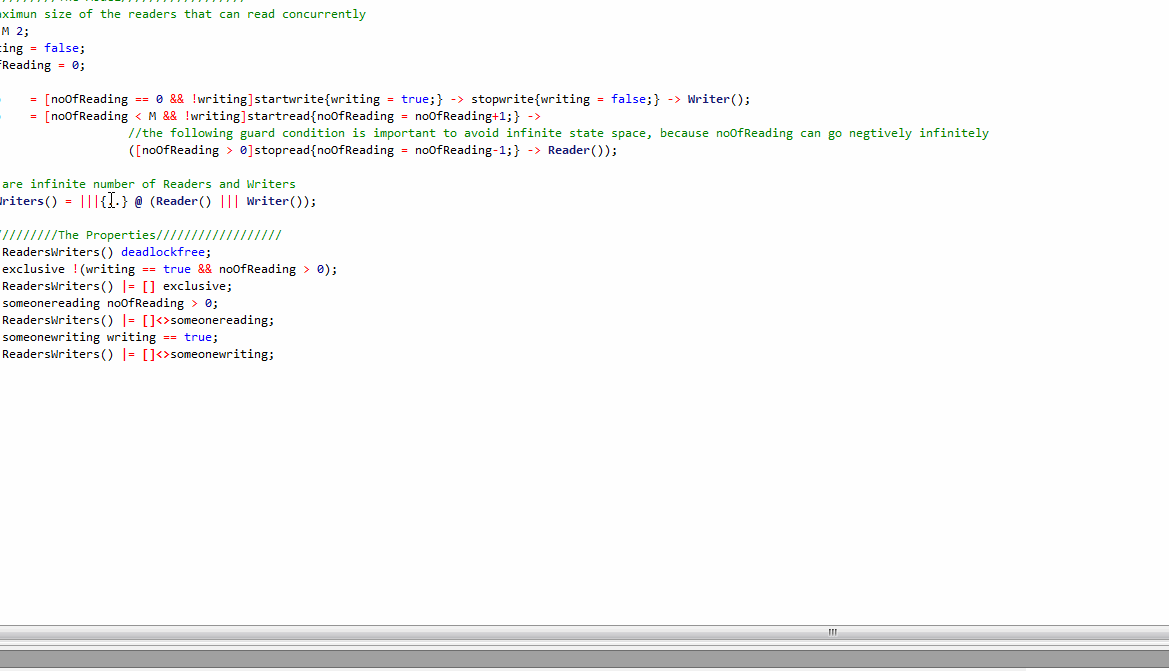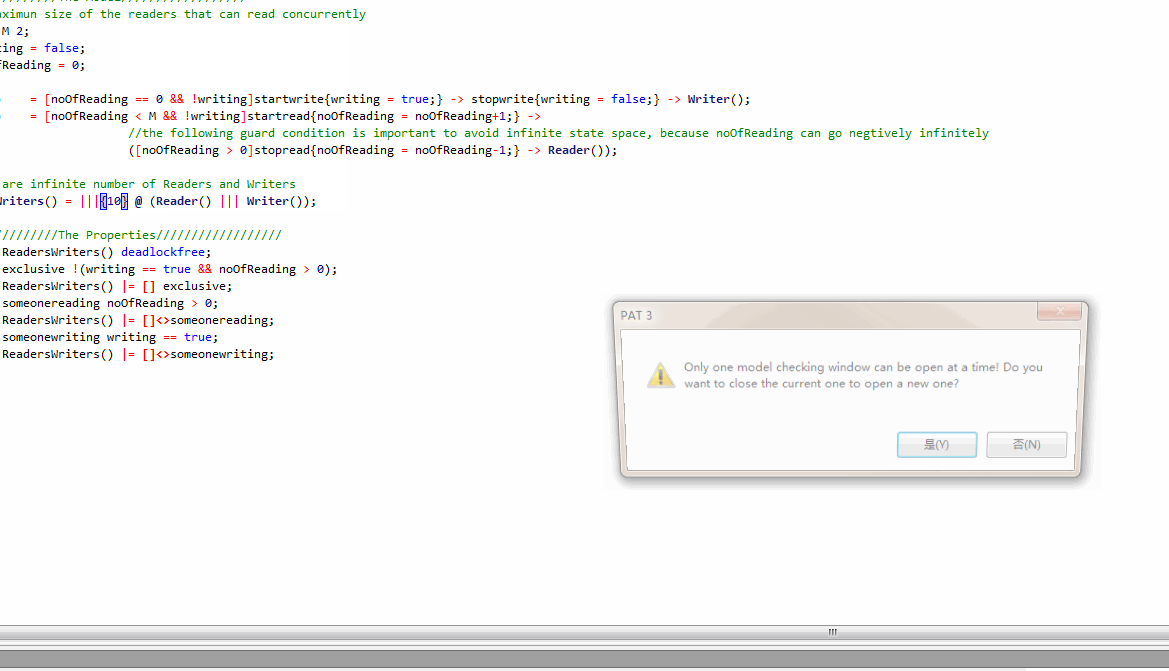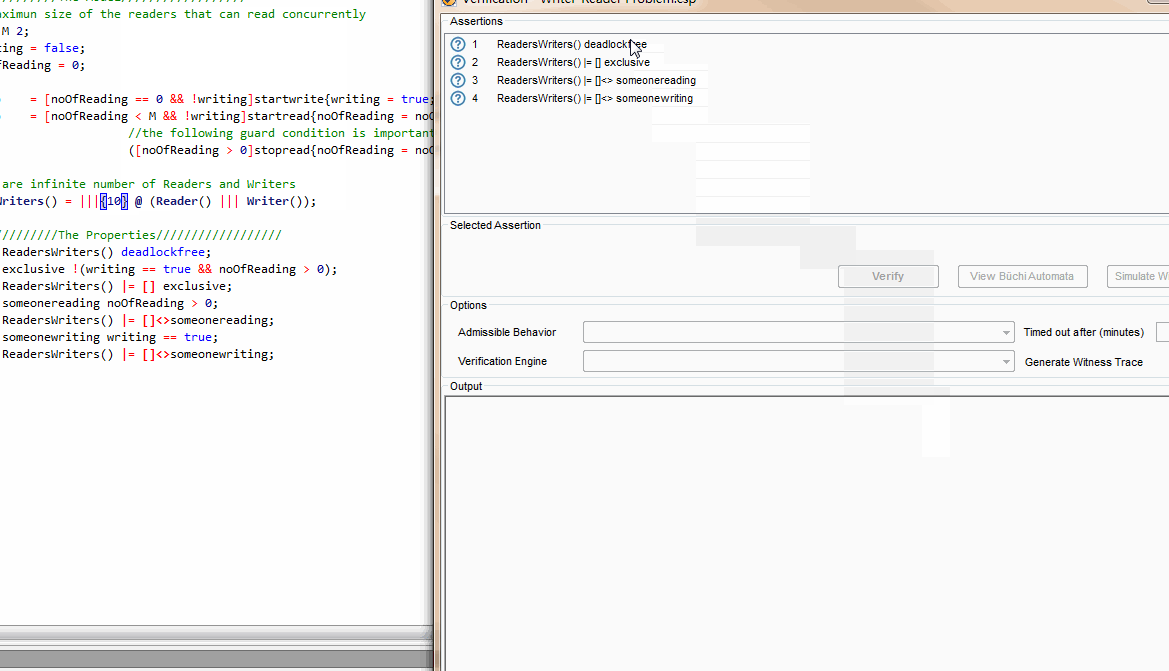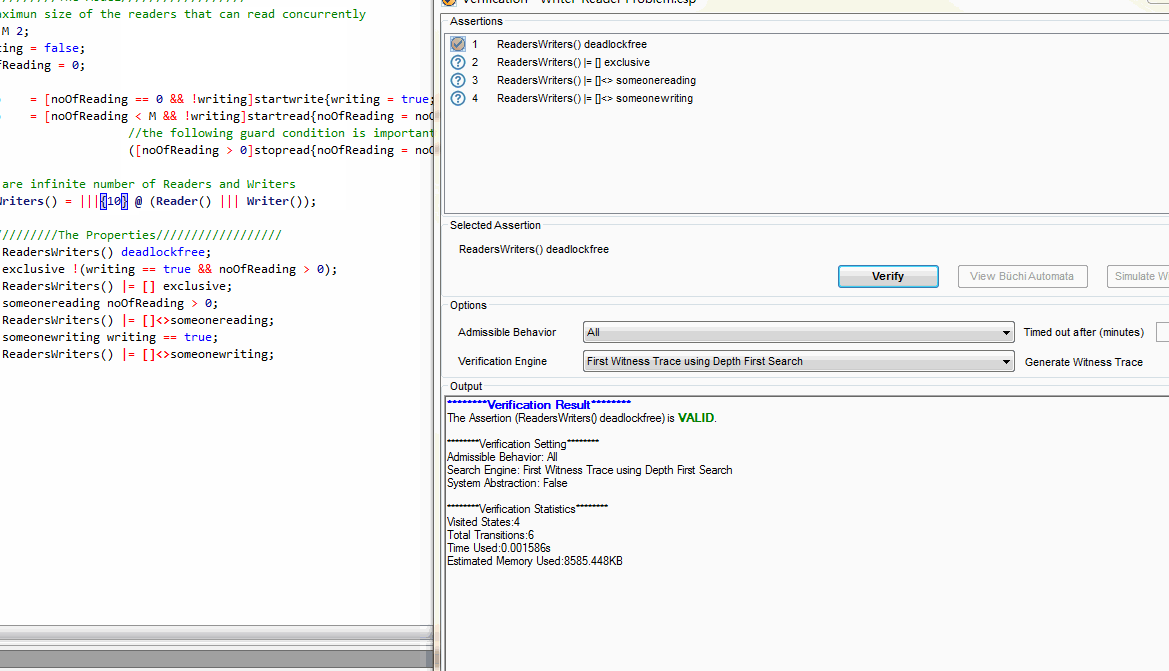
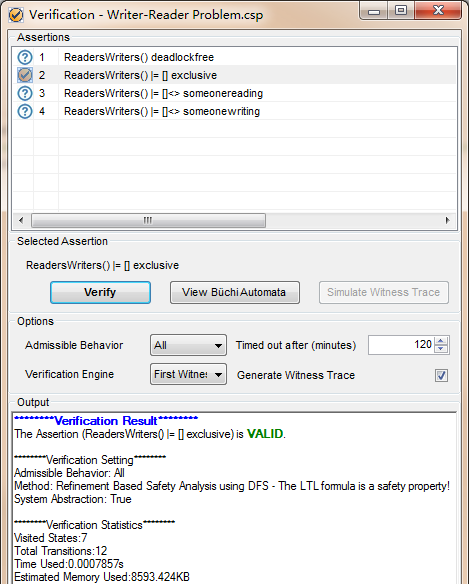
接下来定义了变量，变量是写为真且读的个数大余0的取反，这个在每个状态都是对的，因为可以写的时候读的必须是0，可以读的时候，必须不能写。所以下面这个验证是对的。

#assert ReadersWriters() |= [] exclusive;

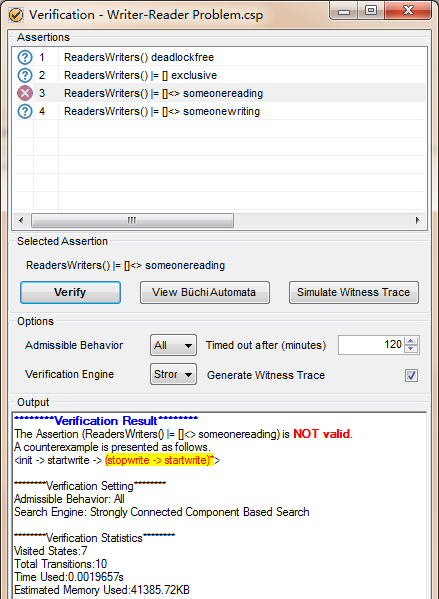
下面两个的验证是不正确的，因为，不一定会总有人在读书或者不一定总有人在写。所以这两个验证都不一定正确。

#define someonereading noOfReading > 0;
#assert ReadersWriters() |= []<>someonereading;
#define someonewriting writing == true;
#assert ReadersWriters() |= []<>someonewriting;

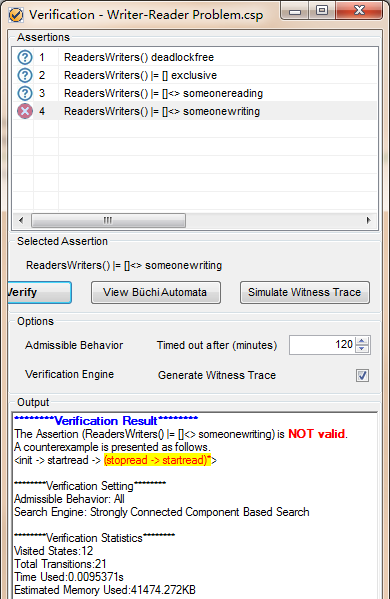
到这里我们这次就结束了。