ch02 课下作业
2.96遵循位级浮点编码规则,实现具有如下原型的函数:
/*
*Compute (int) f.
*If conversion causes overflow or f is NaN, return
*/
int float_f2i(float bits f);
对于浮点数f,这个函数计算(int)f。如果f是NaN,你的函数应该向零舍人。如果f不能用整数表示(例如,超出表示范围,或者它是一个NaN),那么函数应该返回。x800000000测试你的函数,对参数f可以取的所有2^32个值求值,将结果与你使用机器的浮点运算得到的结果相比较。
代码:
#include <stdio.h>
typedef unsigned float_bits;
int float_f2i(float_bits f){
unsigned sign, exp, frac, last_bit;
int i;
sign = f >> 31;
exp = (f >> 23) & 0xff;
frac = f & 0x7fffff;
if (exp == 158 && frac == 0 && sign == 1)
i = 0x80000000;
else if (exp > 157 || exp == 0xff)
i = 0x80000000;
else if (exp < 126)
i = 0;
else{
exp -= 127;
frac |= 0x800000;
if (exp > 23){
exp -= 23;
frac <<= exp;
}else if (exp < 23){
exp = 23 - exp;
frac >>= exp;
}
if (sign == 1)
i = (~frac) + 1;
else
i = frac;
}
return i;
}
void main(){
float f;
unsigned i;
int j, k;
for (i = 0x3fbfff70U; i <= 0xffffffffU; i++)
{
f = *(float *)&i;
j = (int)f;
k = float_f2i(i);
printf("原值:%f \t 机器运算:%d \t 函数运算:%d\n", f, j, k);
}
}
运行结果:
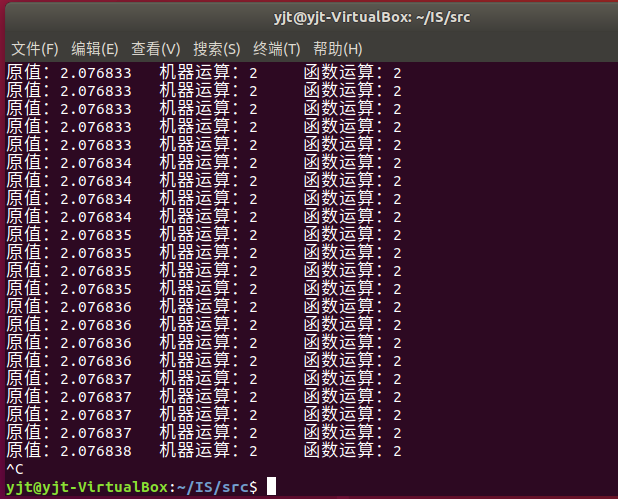
2.97
遵循位级浮点编码规则,实现具有如下原型的函数:
/*Compute (float) i*/
float bits float_i2f(int i);
对于函数i,这个函数计算(float) i的位级表示。
测试你的函数,对参数f可以取的所有2^32个值求值,将结果与你使用机器的浮点运算得到的
结果相比较。
代码:
#include <stdio.h>
typedef unsigned float_bits;
typedef unsigned char *byte_pointer;
void show_bytes(byte_pointer start, size_t len) {
size_t i;
for(i=0; i<len; i++)
printf(" %.2x", start[i]);
printf("\t");
}
float_bits float_i2f(int x) {
unsigned shiftLeft=0;
unsigned afterShift, tmp, flag;
unsigned absX=x;
unsigned sign=0;
if (x==0)
return 0;
if (x<0){
sign=0x80000000;
absX=-x;
}
afterShift=absX;
while (1){
tmp=afterShift;
afterShift<<=1;
shiftLeft++;
if (tmp & 0x80000000)
break;
}
if ((afterShift & 0x01ff)>0x0100)
flag=1;
else if ((afterShift & 0x03ff)==0x0300)
flag=1;
else
flag=0;
return sign+(afterShift>>9)+((159-shiftLeft)<<23)+flag;
}
void main(){
int x;
unsigned i,k;
float j;
for (i = 0x3fbfff70U; i <= 0xffffffffU; i++){
x = *(int *)&i;
printf("原值:");
show_bytes((byte_pointer) &x, sizeof(int));
j=(float)i;
printf("机器运算:");
show_bytes((byte_pointer) &j, sizeof(float));
k=float_i2f(i);
printf("函数运算:");
show_bytes((byte_pointer) &k, sizeof(unsigned));
printf("\n");
}
}
运行结果: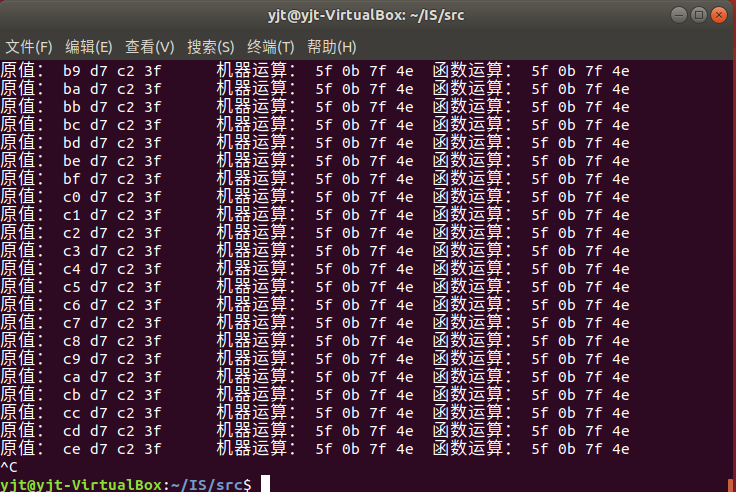
ch02 课下作业的更多相关文章
- 2018-2019-1 20165205 ch02 课下作业
ch02 课下作业 2.96 代码 #include <stdio.h> #include <stdlib.h> typedef unsigned float_bits; fl ...
- 20165302 ch02 课下作业
20165302 ch02 课下作业 作业内容 补充完成课上测试(不能只有截图,要有分析,问题解决过程,新学到的知识点) 完成教材 p97 2.96 2.97,要有完备的测试 发一篇相关内容的博客, ...
- 20155212 ch02 课下作业
20155212 ch02 课下作业 T1 题目 参考附图代码,编写一个程序 "week0601学号.c",判断一下你的电脑是大端还是小端 相关知识 小端法:最低有效字节在最前面 ...
- 2018-2019-1 20165330 《信息安全系统设计基础》第六周课上测试ch02&课下作业
课上测试 测试-3-ch02 任务详情 编写一个程序 "week0203学号.c",运行下面代码: 1 short int v = -学号后四位 2 unsigned short ...
- 20165311 ch02 课下作业
补充完成课上测试(不能只有截图,要有分析,问题解决过程,新学到的知识点) 完成教材 p97 2.96 2.97,要有完备的
- 20155331 ch02 课下作业
2.96 遵循位级浮点编码规则,实现具有如下原型的函数: /* *Compute (int)f. *If conversion cause overflow or f is NaN, return 0 ...
- 20155338 ch02 ch03课下作业
20155338 ch02 ch03课下作业 要求: 1.补充完成课上测试(不能只有截图,要有分析,问题解决过程,新学到的知识点) 课上测试-3-ch02 1.编写一个程序 "week060 ...
- 20175221 MyCP(课下作业,必做)
MyCP(课下作业,必做) 任务详情 编写MyCP.java 实现类似Linux下cp XXX1 XXX2的功能,要求MyCP支持两个参数: - java MyCP -tx XXX1.txt XXX2 ...
- 20175221 《Java程序设计》迭代和JDB(课下作业,选做):
20175221 <Java程序设计> 迭代和JDB(课下作业,选做): 任务详情 1 使用C(n,m)=C(n-1,m-1)+C(n-1,m)公式进行递归编程实现求组合数C(m,n)的功 ...
随机推荐
- canvas-简单快速实现知乎登录页背景效果
前言 打开知乎的登录页,就可以看到其背景有一个动效,看起来好像蛮不错的样子: 这个效果使用canvas是不难实现的,接下来就一步一步地讲解并实现这个效果. 分析 在动工之前先分析这个效果到底是如何运动 ...
- Oracle错误——ORA-12704:字符集不匹配
错误 在查询使用coalesce把字符串进行转换时,报错ORA-12704:字符集不匹配 如下图 解决方法 在网上找了很多方法,有使用Translate转换的:有使用to_char()的,经过测试不符 ...
- Ubuntu package system is broken
原文链接安装软件的时候出现错误,遇到包管理系统损坏的问题.在askubuntu上找到解决办法,这里进行记录总结:首先:sudo apt-get -f install 强制安装没有下载完成的文件.然后: ...
- CF1131D tarjan,拓扑
题目链接 541div2 http://codeforces.com/contest/1131/problem/D 思路 给出n序列和m序列的相对大小关系 构造出最大值最小的序列 缩点+拓扑 小的向大 ...
- 三部排序|2013年蓝桥杯B组题解析第六题-fishers
三部排序| 一般的排序有许多经典算法,如快速排序.希尔排序等. 但实际应用时,经常会或多或少有一些特殊的要求.我们没必要套用那些经典算法,可以根据实际情况建立更好的解法. 比如,对一个整型数组中的数字 ...
- FJUT 聪明的商人(树上倍增)题解
思路:求树上两点的距离,显然是dep[u] + dep[v] - 2 * dep[lca],用树上倍增去写. 参考:树上倍增的写法和应用(详细讲解,新手秒懂) 代码: #include<set& ...
- Chrome上的扩展工具
rest client - rest api Testing:类似fiddler的工具,可以测试url,查看返回值……
- Ubuntu 18.04版本下安装网易云音乐
这是我迄今为止发现的最完美的解决方法,不用改任何东西,只需要安装然后打开即可,后台也有. 参考:http://archive.ubuntukylin.com:10006/ubuntukylin/poo ...
- 【NOIP 2016】Day2 T3 愤怒的小鸟
Problem Description \(Kiana\) 最近沉迷于一款神奇的游戏无法自拔. 简单来说,这款游戏是在一个平面上进行的. 有一架弹弓位于 \((0,0)\) 处,每次 \(Kiana\ ...
- Java单例设计模式(实现Java的一个类只有一个对象)
单例设计模式的定义:单例设计模式是一种软件设计模式,在它的核心包含一个称为单例类的核心类. 核心便是希望一个类只有一个对象. 如何实现类在内存中只有一个对象呢? 第一步:构造私有:第二步:本身提供一 ...
