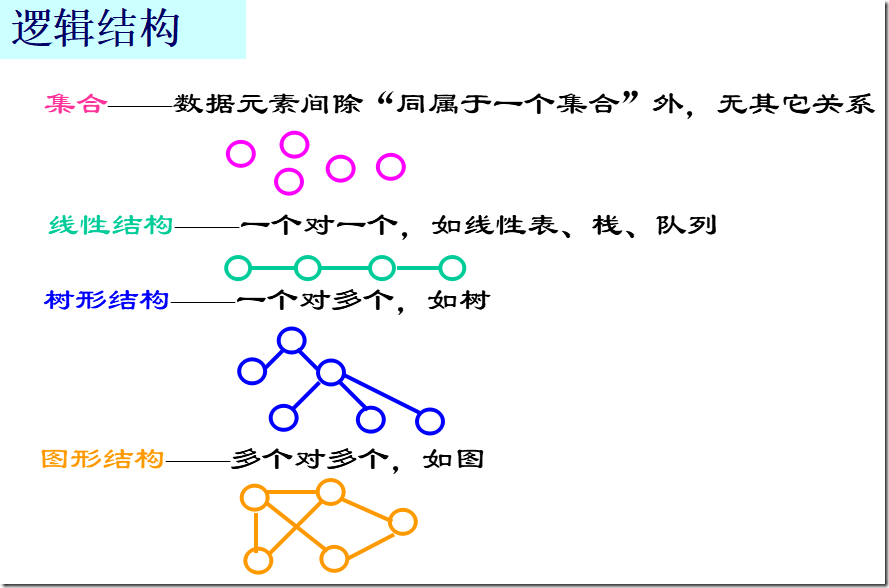
数据结构(C语言版)-第5章 树和二叉树
5.1 树和二叉树的定义
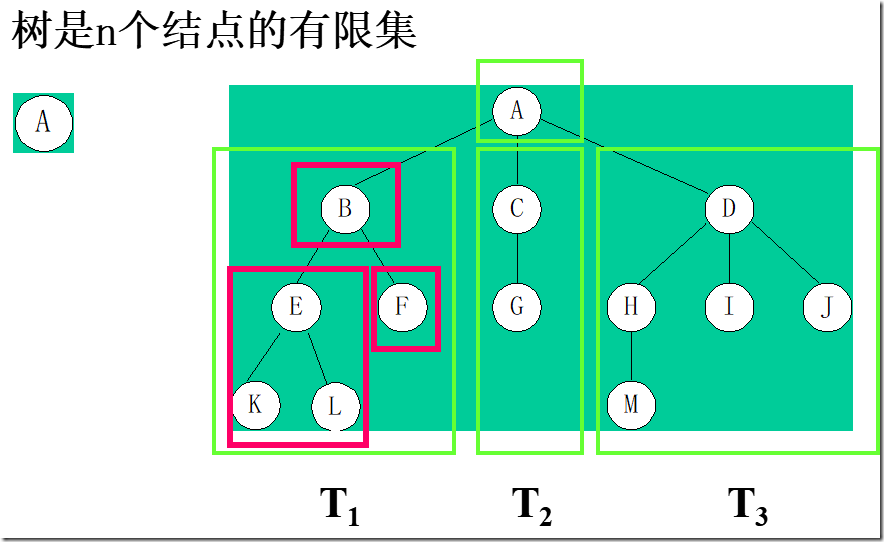
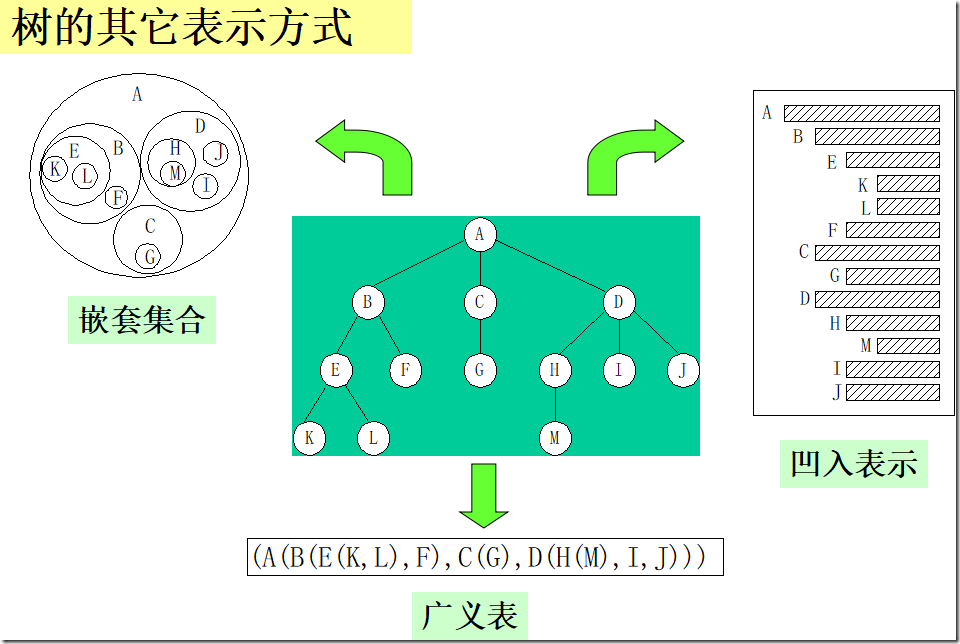
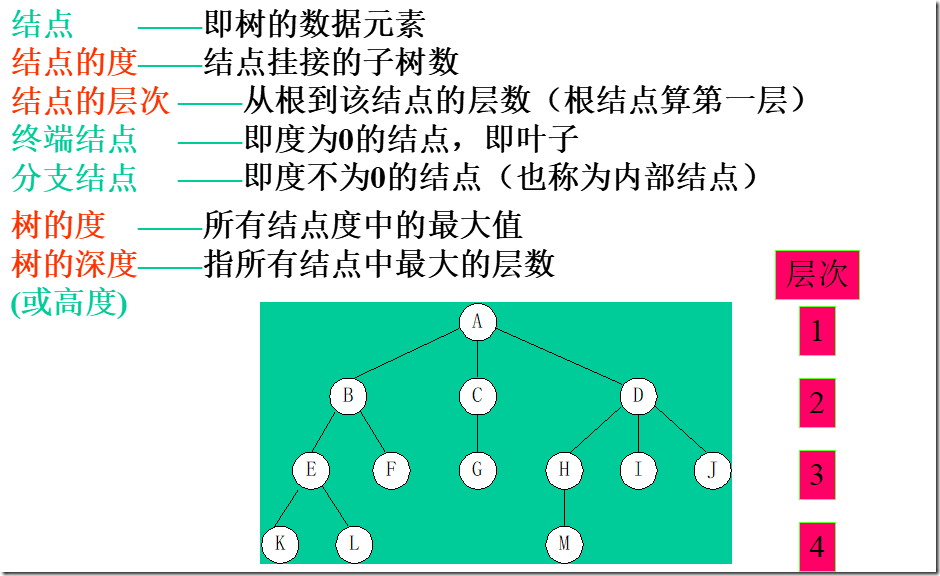
树(Tree)是n(n≥0)个结点的有限集,它或为空树(n = 0);或为非空树,对于非空树T:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点可分为m(m>0)个互不相交的有限集T1, T2, …, Tm, 其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。



二叉树的定义
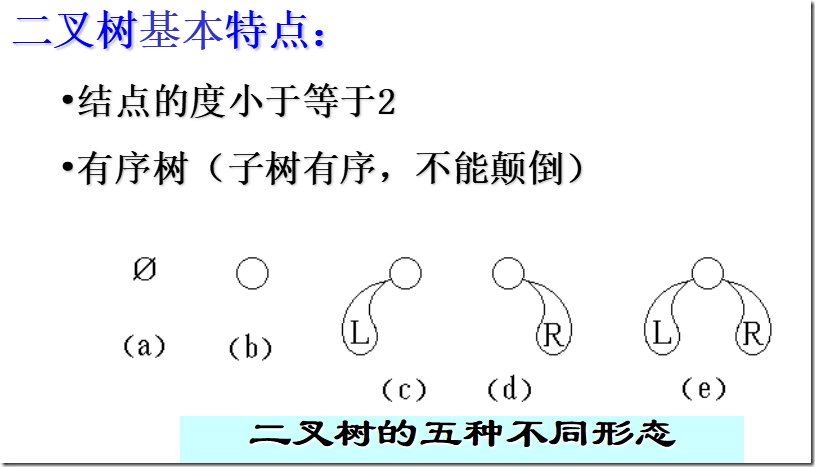
二叉树(Binary Tree)是n(n≥0)个结点所构成的集合,它或为空树(n = 0);或为非空树,对于非空树T:
(1)有且仅有一个称之为根的结点;
(2)除根结点以外的其余结点分为两个互不相交的子集T1和T2,分别称为T的左子树和右子树,且T1和T2本身又都是二叉树。
为何要重点研究每结点最多只有两个 “叉” 的树?
二叉树的结构最简单,规律性最强;
可以证明,所有树都能转为唯一对应的二叉树,不失一般性。
5.2 案例引入
无
5.3 树和二叉树的抽象数据类型定义
CreateBiTree(&T,definition)
初始条件;definition给出二叉树T的定义。
操作结果:按definition构造二叉树T。
PreOrderTraverse(T)
初始条件:二叉树T存在。
操作结果:先序遍历T,对每个结点访问一次。
InOrderTraverse(T)
初始条件:二叉树T存在。
操作结果:中序遍历T,对每个结点访问一次。
PostOrderTraverse(T)
初始条件:二叉树T存在。
操作结果:后序遍历T,对每个结点访问一次。
5.4 二叉树的性质和存储结构


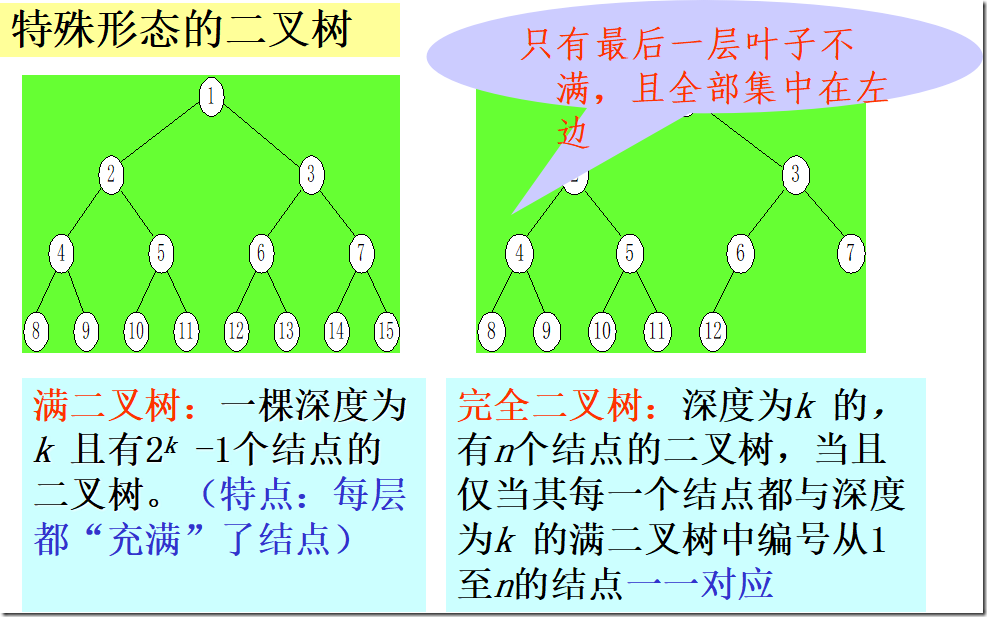
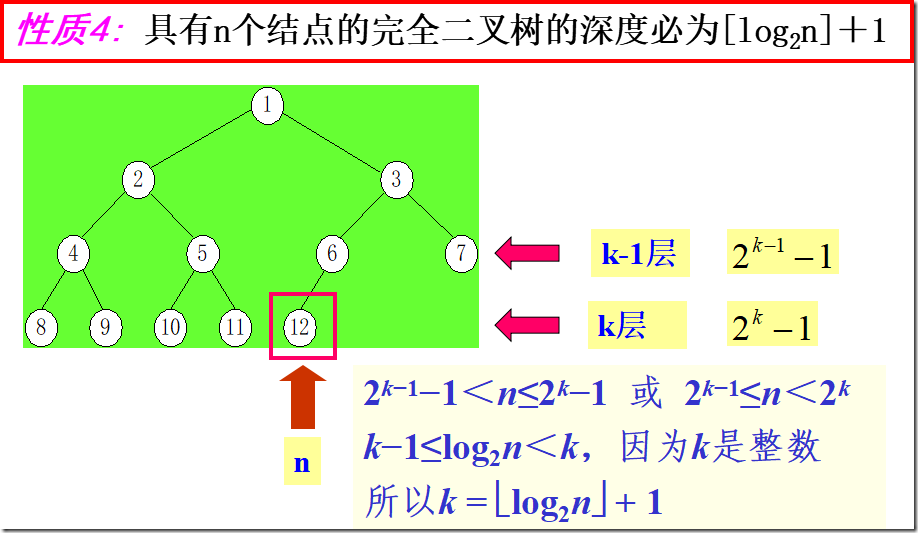
满二叉树是叶子一个也不少的树,而完全二叉树虽然前n-1层是满的,但最底层却允许在右边缺少连续若干个结点。满二叉树是完全二叉树的一个特例。

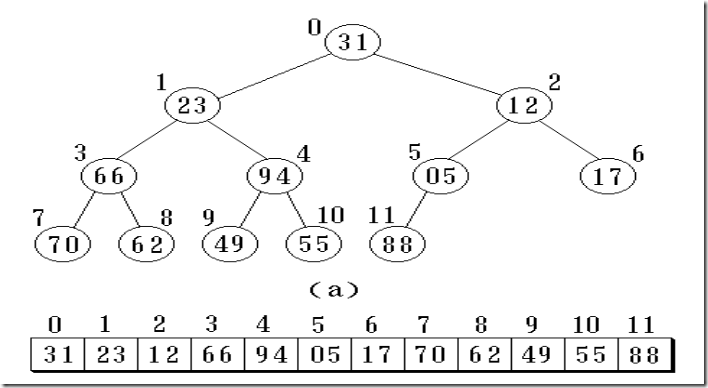
二叉树的顺序存储
实现:按满二叉树的结点层次编号,依次存放二叉树中的数据元素。
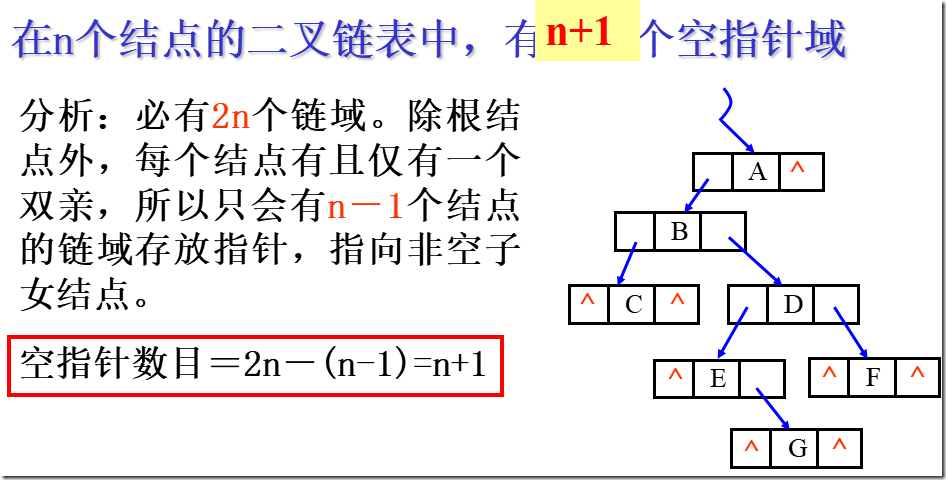
二叉树的链式存储

typedef struct BiNode{
TElemType data;
struct BiNode *lchild,*rchild; //左右孩子指针
}BiNode,*BiTree;
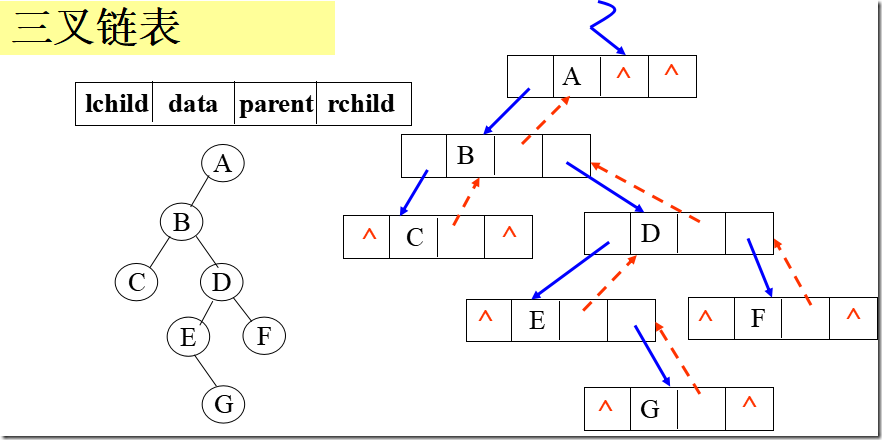
typedef struct TriTNode
{ TelemType data;
struct TriTNode *lchild,*parent,*rchild;
}TriTNode,*TriTree;
5.5 遍历二叉树和线索二叉树
遍历定义——指按某条搜索路线遍访每个结点且不重复(又称周游)。
遍历用途——它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
遍历规则
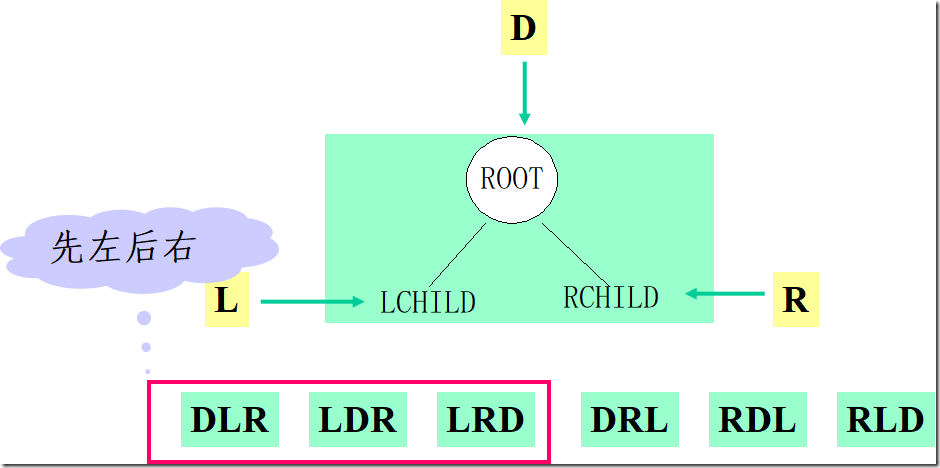
口诀:
DLR—先序遍历,即先根再左再右
LDR—中序遍历,即先左再根再右
LRD—后序遍历,即先左再右再根
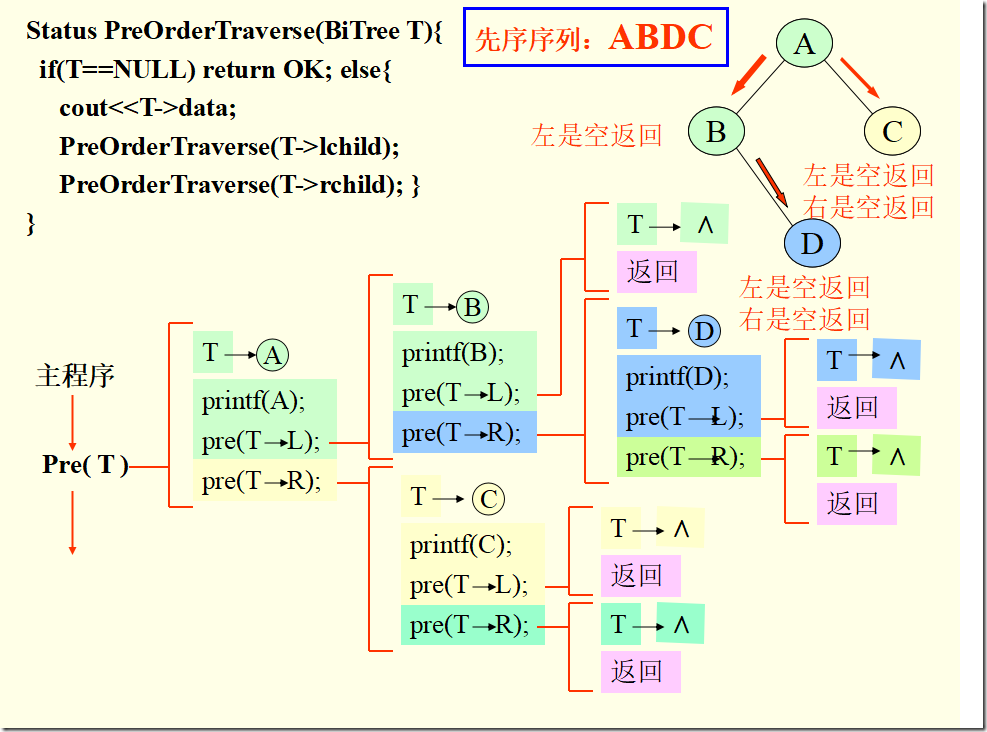
先序遍历算法
Status PreOrderTraverse(BiTree T){
if(T==NULL) return OK; //空二叉树
else{
cout<<T->data; //访问根结点
PreOrderTraverse(T->lchild); //递归遍历左子树
PreOrderTraverse(T->rchild); //递归遍历右子树
}
}
中序遍历算法
Status InOrderTraverse(BiTree T){
if(T==NULL) return OK; //空二叉树
else{
InOrderTraverse(T->lchild); //递归遍历左子树
cout<<T->data; //访问根结点
InOrderTraverse(T->rchild); //递归遍历右子树
}
}
后序遍历算法
Status PostOrderTraverse(BiTree T){
if(T==NULL) return OK; //空二叉树
else{
PostOrderTraverse(T->lchild); //递归遍历左子树
PostOrderTraverse(T->rchild); //递归遍历右子树
cout<<T->data; //访问根结点
}
}
时间效率:O(n) //每个结点只访问一次
空间效率:O(n) //栈占用的最大辅助空间
二叉树的建立
void CreateBiTree(BiTree &T){
cin>>ch;
if (ch==’#’) T=NULL; //递归结束,建空树
else{
T=new BiTNode; T->data=ch; //生成根结点
CreateBiTree(T->lchild); //递归创建左子树
CreateBiTree(T->rchild); //递归创建右子树
}
}
二叉树遍历算法的应用

int NodeCount(BiTree T){
if(T == NULL ) return 0;
else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
}

int LeadCount(BiTree T){
if(T==NULL) //如果是空树返回0
return 0;
if (T->lchild == NULL && T->rchild == NULL)
return 1; //如果是叶子结点返回1
else return LeadCount(T->lchild) + LeadCount(T->rchild);
}

二叉链表空间效率这么低,能否利用这些空闲区存放有用的信息或线索?
——可以用它来存放当前结点的直接前驱和后继等线索,以加快查找速度。
线索化二叉树

先序线索二叉树
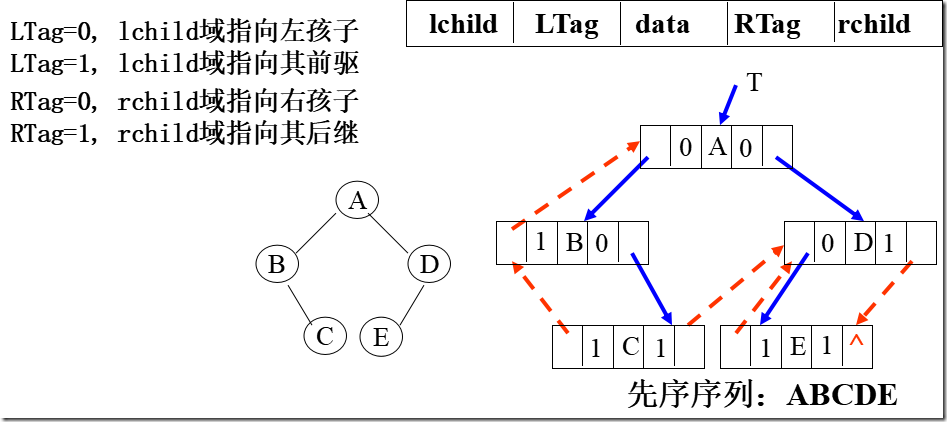
中序线索二叉树
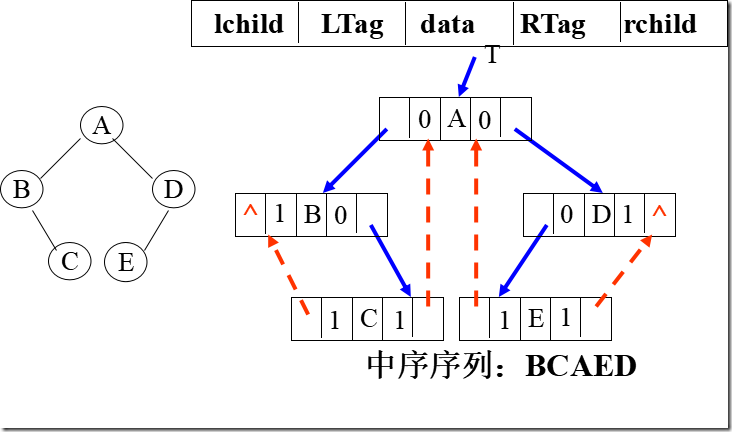
后序线索二叉树
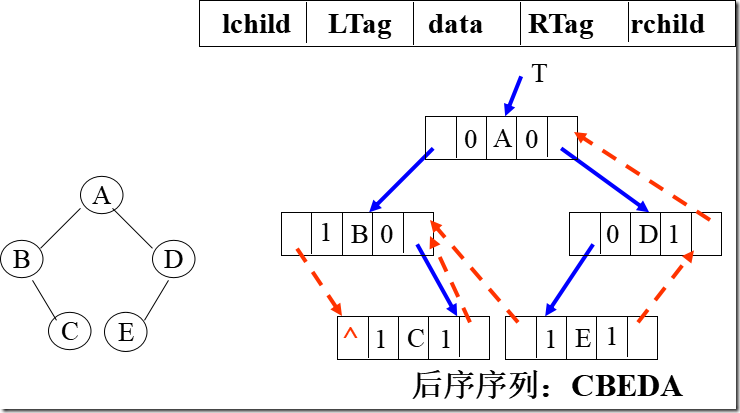
5.6 树和森林
树的存储结构--二叉链表表示法
typedef struct CSNode{
ElemType data;
struct CSNode *firstchild,*nextsibling;
}CSNode,*CSTree;
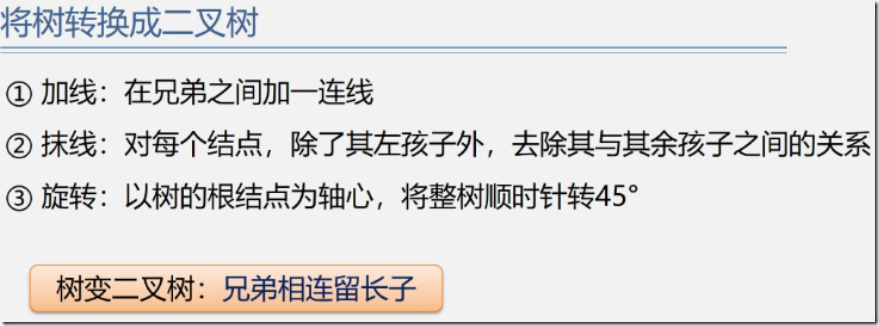
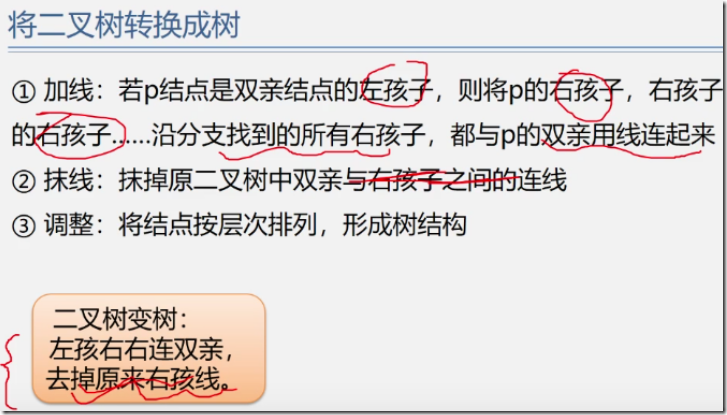
树和森林的转换。。。



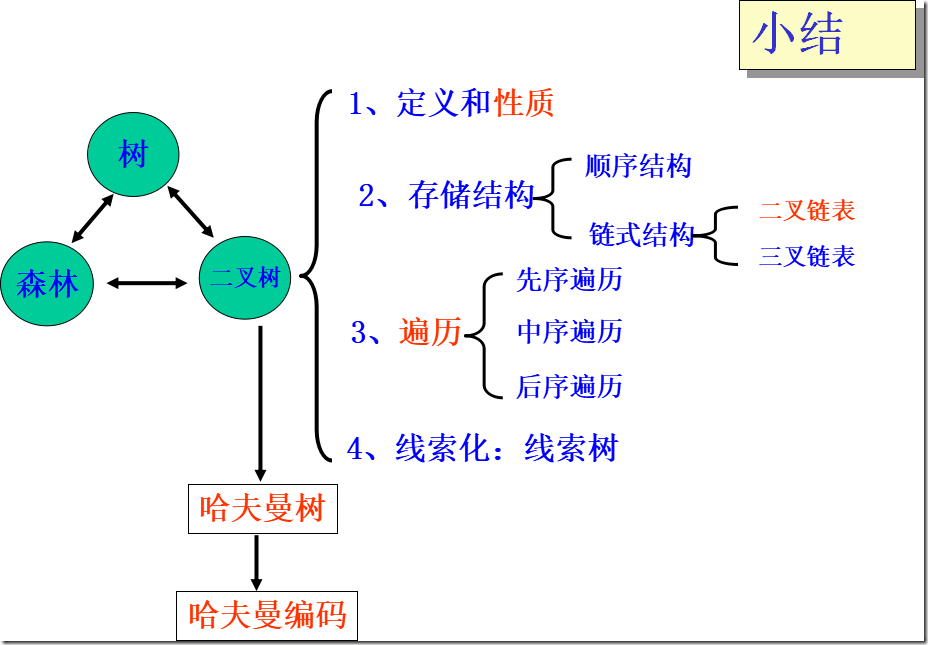
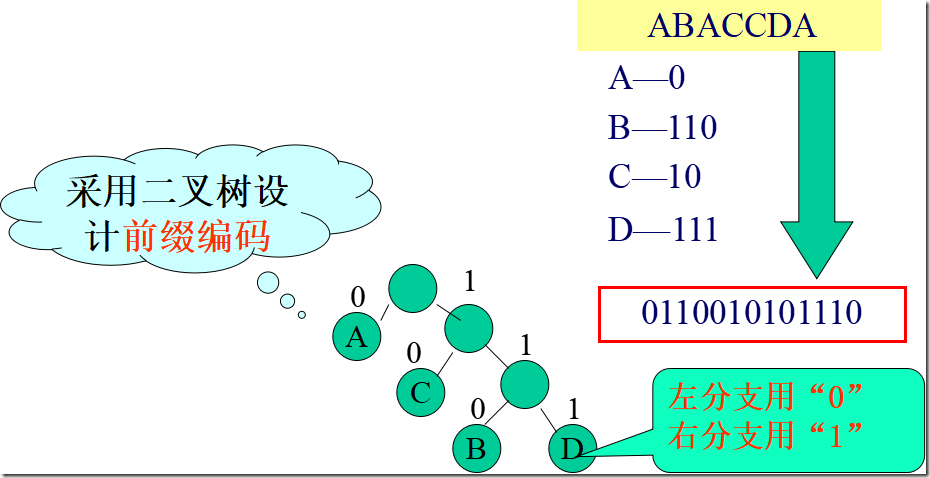
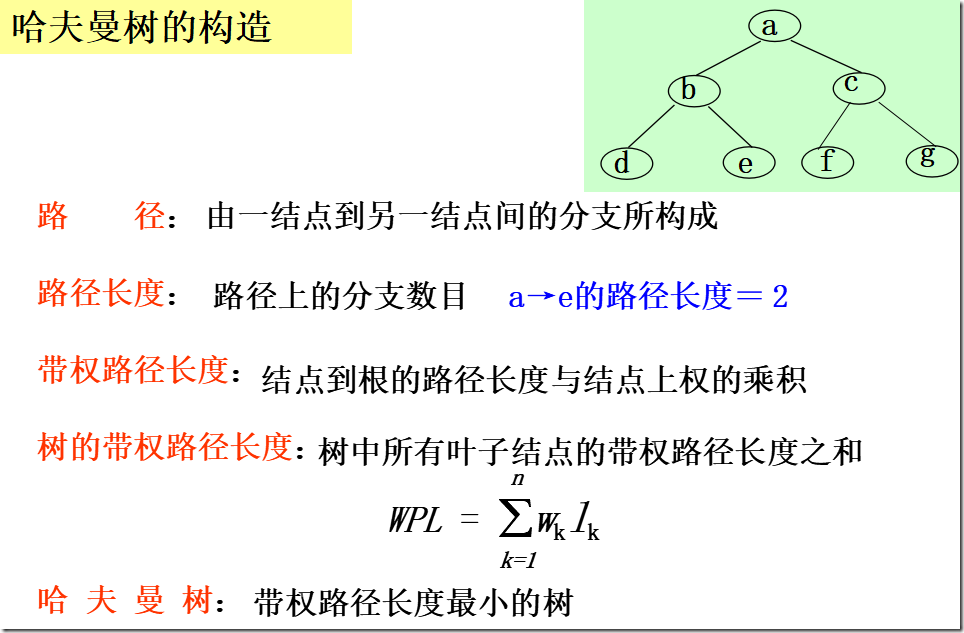
5.7 哈夫曼树及其应用
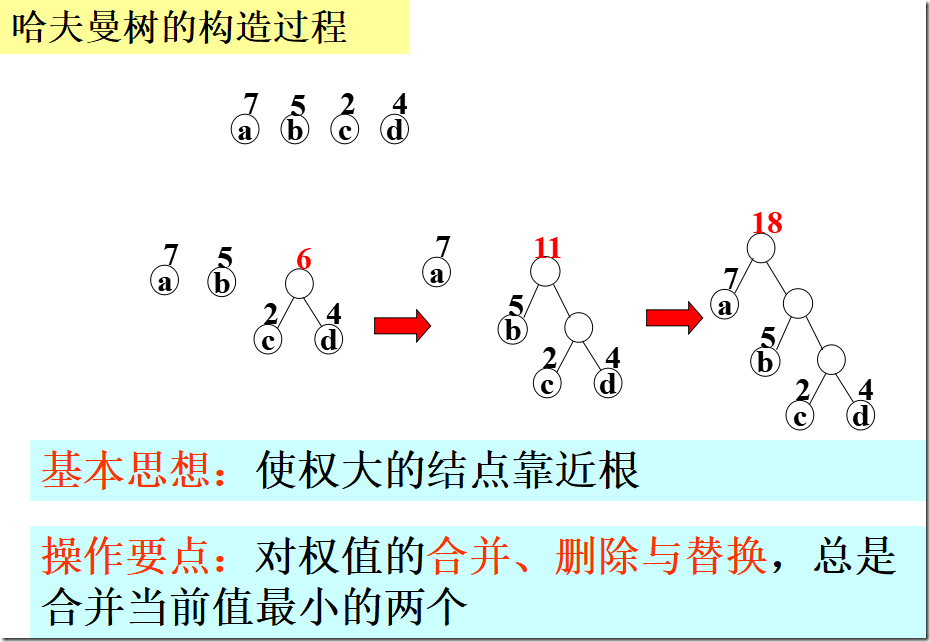
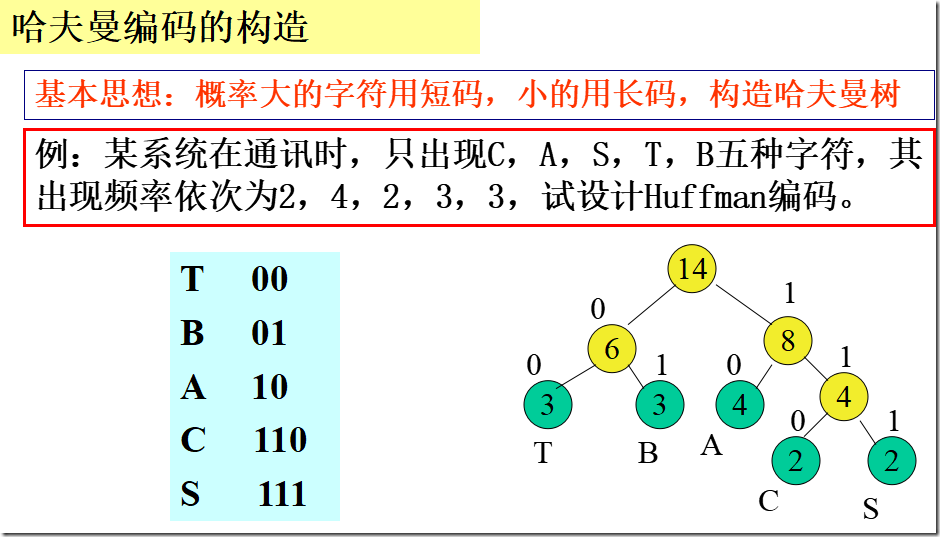

。。。。。
数据结构(C语言版)-第5章 树和二叉树的更多相关文章
- 深入浅出数据结构C语言版(10)——树的简介
到目前为止,我们一直在谈论的数据结构都是"线性结构",不论是普通链表.栈还是队列,其中的每个元素(除了第一个和最后一个)都只有一个前驱(排在前面的元素)和一个后继(排在后面的元素) ...
- c++学习书籍推荐《清华大学计算机系列教材:数据结构(C++语言版)(第3版)》下载
百度云及其他网盘下载地址:点我 编辑推荐 <清华大学计算机系列教材:数据结构(C++语言版)(第3版)>习题解析涵盖验证型.拓展型.反思型.实践型和研究型习题,总计290余道大题.525道 ...
- 《数据结构-C语言版》(严蔚敏,吴伟民版)课本源码+习题集解析使用说明
<数据结构-C语言版>(严蔚敏,吴伟民版)课本源码+习题集解析使用说明 先附上文档归类目录: 课本源码合辑 链接☛☛☛ <数据结构>课本源码合辑 习题集全解析 链接☛☛☛ ...
- 数据结构C语言版 有向图的十字链表存储表示和实现
/*1wangxiaobo@163.com 数据结构C语言版 有向图的十字链表存储表示和实现 P165 编译环境:Dev-C++ 4.9.9.2 */ #include <stdio.h> ...
- 数据结构C语言版 表插入排序 静态表
数据结构C语言版 表插入排序.txt两个人吵架,先说对不起的人,并不是认输了,并不是原谅了.他只是比对方更珍惜这份感情./* 数据结构C语言版 表插入排序 算法10.3 P267-P270 编译 ...
- 数据结构C语言版 弗洛伊德算法实现
/* 数据结构C语言版 弗洛伊德算法 P191 编译环境:Dev-C++ 4.9.9.2 */ #include <stdio.h>#include <limits.h> # ...
- 数据结构(c语言版)文摘
第一章 绪论 数据结构:是一门研究非数值计算的程序设计问题中计算机的操作对象以及它们之间的关系和操作等的学科. 数据:是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序处理 ...
- 数据结构( Pyhon 语言描述 ) — —第10章:树
树的概览 树是层级式的集合 树中最顶端的节点叫做根 个或多个后继(子节点). 没有子节点的节点叫做叶子节点 拥有子节点的节点叫做内部节点 ,其子节点位于层级1,依次类推.一个空树的层级为 -1 树的术 ...
- 深入浅出数据结构C语言版(12)——平衡二叉查找树之AVL树
在上一篇博文中我们提到了,如果对普通二叉查找树进行随机的插入.删除,很可能导致树的严重不平衡 所以这一次,我们就来介绍一种最老的.可以实现左右子树"平衡效果"的树(或者说算法),即 ...
随机推荐
- win7 powershell配色方案
首先我是参考微软的word的, look~ Windows PowerShell 配置文件 要配置powershell很简单, 就几步 1.显示 Windows PowerShell 配置文件的路径 ...
- [c/c++] programming之路(8)、汇编、求模、自增自减
一.插入汇编 #include<stdio.h> void main(){ ; num=num+; //插入汇编语言 _asm{ mov eax,num;//eax是一个存储器,将num的 ...
- MFC限制edit控件的字符输入长度
一. 1.Edit 控件添加EN_CHANGE事件 #define MAX_SIZE 200 void CMyDlg::OnChangeEditFeed() { // TODO: 如果该控件是 RIC ...
- SVM学习笔记2-拉格朗日对偶
下面我们抛开1中的问题.介绍拉格朗日对偶.这一篇中的东西都是一些结论,没有证明. 假设我们有这样的问题:$min_{w}$ $f(w)$,使得满足:(1)$g_{i}(w)\leq 0,1\leq i ...
- 小C的数学问题 【单调栈】
问题 J: 小C的数学问题 时间限制: 1 Sec 内存限制: 128 MB 提交: 565 解决: 141 [提交] [状态] [命题人:外部导入] 题目描述 小C是个云南中医学院的大一新生,在 ...
- apache安装时的一些术语
apache源码安装时,需要的哪些必须依赖模块? 主要需要apr, apr-util, pcre模块 其中 apr模块时必须的. 如何卸载 源码安装的软件? 在源码 的 解压目录下, 使用 make ...
- java 之 dom4j解析xml
*dom4j,是一个组织,针对xml解析,提供解析器dom4j *dom4j不是javase的一部分,想要使用需要导入dom4j提供的jar包 *第一步:创建lib文件夹,将压缩文件放到此处 *第二步 ...
- maven下载jar包下载不下来的解决方法
转载请注明出处: 在eclipse中安装了maven插件,项目在运行的时候,一直通过pom.xml文件下载jar包,一直下载不下来, 在更新maven库时,如果网络问不定或者是一些自己手动安装到本地m ...
- log4j2打印Mybatis执行的SQL语句及SQL语句的执行时间
http://blog.csdn.net/zjq852533445/article/details/78320012
- 4、lvs nat和dr类型演示
实战操作 LVS-NAT (应用场景:VIP是公网地址,DIP和RIP一般使用私网地址,NAT的主要目的是为了隐藏服务器) 核心要点: 1.DIP与各real server的RIP必须在同一个网段中 ...