P1192 台阶问题
递推问题,要用到递推式:
设f(n)为n个台阶的走法总数,把n个台阶的走法分成k类:
第1类:第1步走1阶,剩下还有n-1阶要走,有f(n-1)种方法;
第2类:第1步走2阶,剩下还有n-2阶要走,有f(n-2)种方法;
第3类:第1步走3阶,剩下还有n-3阶要走,有f(n-3)种方法;
.......... ...........
第k类:第1步走k阶,剩下还有n-k阶要走,有f(n-k)种方法;
根据加法原理:f(n)=f(n-1)+f(n-2)+.......+f(n-k)
程序如下:
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cstring>
#include<string>
using namespace std;
int f[];
int main()
{
int n,k;
cin>>n>>k;
f[]=;
for(int i=;i<=n;i++)
for(int j=;j<=k&&i-j>=;j++) //i-j>=0必须要有
{
f[i]+=f[i-j];
f[i]%=;
}
cout<<f[n];
return ;
}
P1192 台阶问题的更多相关文章
- 洛谷 P1192 台阶问题
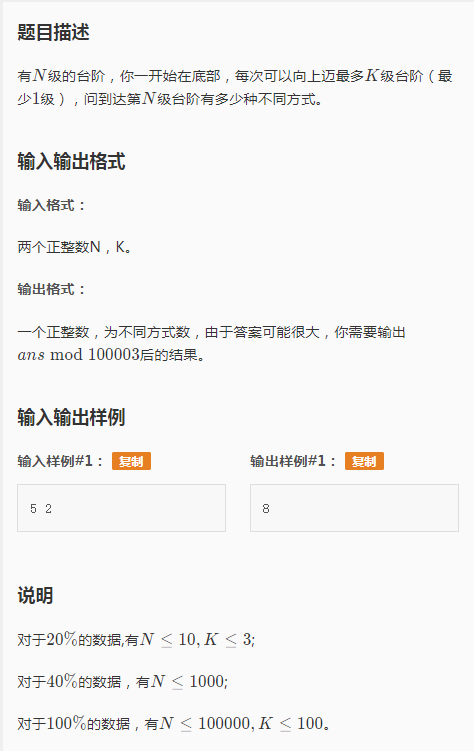
P1192 台阶问题 题目描述 有N级的台阶,你一开始在底部,每次可以向上迈最多K级台阶(最少1级),问到达第N级台阶有多少种不同方式. 输入输出格式 输入格式: 输入文件的仅包含两个正整数N,K. ...
- TYVJ P1015 公路乘车 &&洛谷 P1192 台阶问题 Label:dp
题目描述 有N级的台阶,你一开始在底部,每次可以向上迈最多K级台阶(最少1级),问到达第N级台阶有多少种不同方式. 输入输出格式 输入格式: 输入文件的仅包含两个正整数N,K. 输出格式: 输入文件s ...
- 洛谷P1192 台阶问题【记忆化搜索】
题目:https://www.luogu.org/problemnew/show/P1192 题意: 给定n和k,一个人一次可以迈1~k步,问走n步有多少种方案. 思路: 本来傻乎乎上来就递归,显然会 ...
- luogu P1192 台阶问题
https://www.luogu.org/problem/show?pid=1192 登楼梯 肯定能想到 dp[i] = dp[i-1] + dp[i-2] + ...+ dp[i-k] 然后想到 ...
- 洛谷P1192 台阶问题【dp递归】
有NN级的台阶,你一开始在底部,每次可以向上迈最多KK级台阶(最少11级),问到达第NN级台阶有多少种不同方式. 输入输出格式 输入格式: 两个正整数N,K. 输出格式: 一个正整数,为不同方式数,由 ...
- 洛谷P1192台阶问题
题目描述 有NN级的台阶,你一开始在底部,每次可以向上迈最多KK级台阶(最少11级),问到达第NN级台阶有多少种不同方式. 输入格式 两个正整数N,K. 输出格式 一个正整数,为不同方式数,由于答案可 ...
- 洛谷P1192台阶问题(DP)
题目描述 有NNN级的台阶,你一开始在底部,每次可以向上迈最多KKK级台阶(最少111级),问到达第NNN级台阶有多少种不同方式. 输入格式 两个正整数N,K. 输出格式 一个正整数,为不同方式数,由 ...
- (递归)P1192 台阶问题
题解: 这其实是变相的斐波那契,观察下列等式: //k=2 : 1 2 3 5 8 13 21 34...... //k=3 : 1 2 4 7 13 24 44 81... //k=4 : 1 2 ...
- 【Luogu】【关卡2-12】递推与递归二分(2017年10月)
任务说明:递推,层层递进,由基础推向顶层.二分不仅可以用来查找数据,还可以确定最合适的值. P1192 台阶问题 有N级的台阶,你一开始在底部,每次可以向上迈最多K级台阶(最少1级),问到达第N级台阶 ...
随机推荐
- 013-并发编程-java.util.concurrent.locks之-AbstractQueuedSynchronizer-用于构建锁和同步容器的框架、独占锁与共享锁的获取与释放
一.概述 AbstractQueuedSynchronizer (简称AQS),位于java.util.concurrent.locks.AbstractQueuedSynchronizer包下, A ...
- html-标签页
<template> <div class="pos-frame"> <div class="pos h100"> < ...
- numpy的searchsorted细品
import numpy as np a= np.arange(20) pos_left = a.searchsorted(3) #也可以写成np.searchsorted(a, 3), 注 ...
- 【UML】NO.49.EBook.5.UML.1.009-【UML 大战需求分析】- 包图(Package Diagram)
1.0.0 Summary Tittle:[UML]NO.49.EBook.1.UML.1.009-[UML 大战需求分析]- 包图(Package Diagram) Style:DesignPatt ...
- [Java in NetBeans] Lesson 03. More Variables / Type Casting
这个课程的参考视频在youtube. 主要学到的知识点有: It is different from python, that "1" only present string &q ...
- 把文本数据转化为json
awk '{for (i=1 ;i<=NF;i++){ printf "\"" $i; if ( i==NF) {printf "\",&quo ...
- node微信公众号开发--设置自定义菜单
var request = require("request"); const querystring = require("querystring"); re ...
- SQL Server2008 R2 数据库镜像实施手册(双机)SQL Server2014同样适用
这篇文章主要介绍了SQL Server2008 R2 数据库镜像实施手册(双机)SQL Server2014同样适用,需要的朋友可以参考下 一.配置主备机 1. 服务器基本信息 主机名称为:HOST_ ...
- Go linux 实践3
Go 的灵魂-goroutine(协程), channel(渠道) 看看吧,不多说了 ************************************************ package ...
- unity3d 第一人称脚本解释MouseLook
using UnityEngine; using System.Collections; /// MouseLook rotates the transform based on the mouse ...
