uvalive 4960 Sensor Network

题意：

给出一个无向图，求一个生成树使得这个生成树的最大边与最小边之差最小，输出这个最小的差值。n的最大值为350。

思路：

这题不看题解想破头也不知道怎么写Orz。

暴力的做法是可以从大到小枚举边作为最小边的权值，求MST，但是复杂度达到了O(n^4)，很显然会T。

考虑在kruskal算法加边的时候，当两个点在同一个连通分量的时候，加入这条边会形成环，这个时候就把环中的最小边去掉，剩下的边就尽可能达到了最大，当前加入的边设为Ea也最大的，然后再找现在生成树中的最小边Eb；当有n-1条边的时候，就形成了一个生成树，就可以利用Ea – Eb去更新答案。

最重要的两个过程是找环和加边。

判断环，用了LCA的思想，但并不是倍增，而是纯粹暴力的dfs。对于一条边的两个点假设为x和y，首先从一个点x开始访问，直到访问到它的祖先，即满足条件par[x] == x，标记这个过程中的所有点；然后从y开始访问，直到访问到它的祖先（同上）或者它自己或某一个祖先被标记了为止，若y访问到祖先都没有点被标记，那么就说明x和y没有公共祖先，那么它们就不在同一个连通分量中，加入这条边就不会形成环。

若找到了环，那么就要求这个环中边的最小值，求法很自然，遍历从x出发到lca的所有边，遍历从y出发到lca的所有边，找出其中的最小边，之后去掉这条边，去掉这条边有个技巧，假设最小边的非父亲点为u，那么去掉这条边时，令par[u] = u，这条边就被去掉了。之后再找最小边即可。

之后就是加边的过程。并查集加边是启发式合并，但是这题的加边是有方向的加边。

假设两个点x和y，如果有其中一个点就是祖先，那么就把这个点连到另外一个点上（如x为祖先点，那么令par[x] = y）。

但是如果两个点都不是祖先，那么就要考虑如何合并，因为一个点不可能同时有两个父亲。

可以考虑从一个点开始访问，直到访问到祖先，将路径上的点全部按访问的顺序记录在一个vector中，之后逆向加边。

再把这个点连到另一个点上。如图：

合并前：

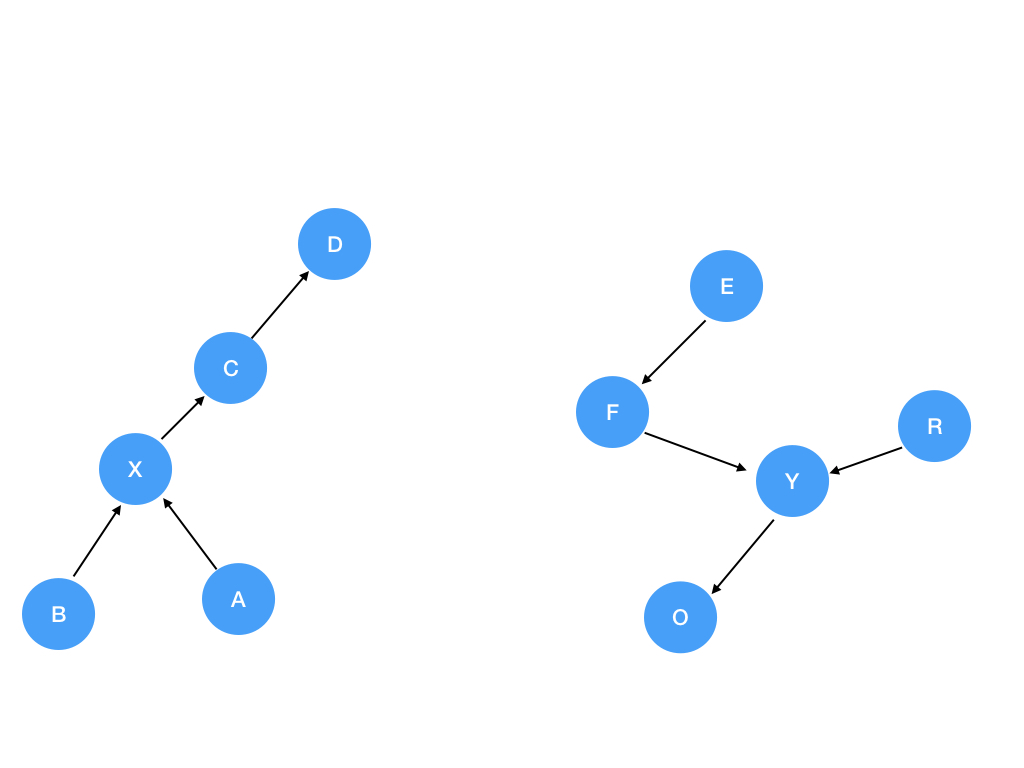
合并后：

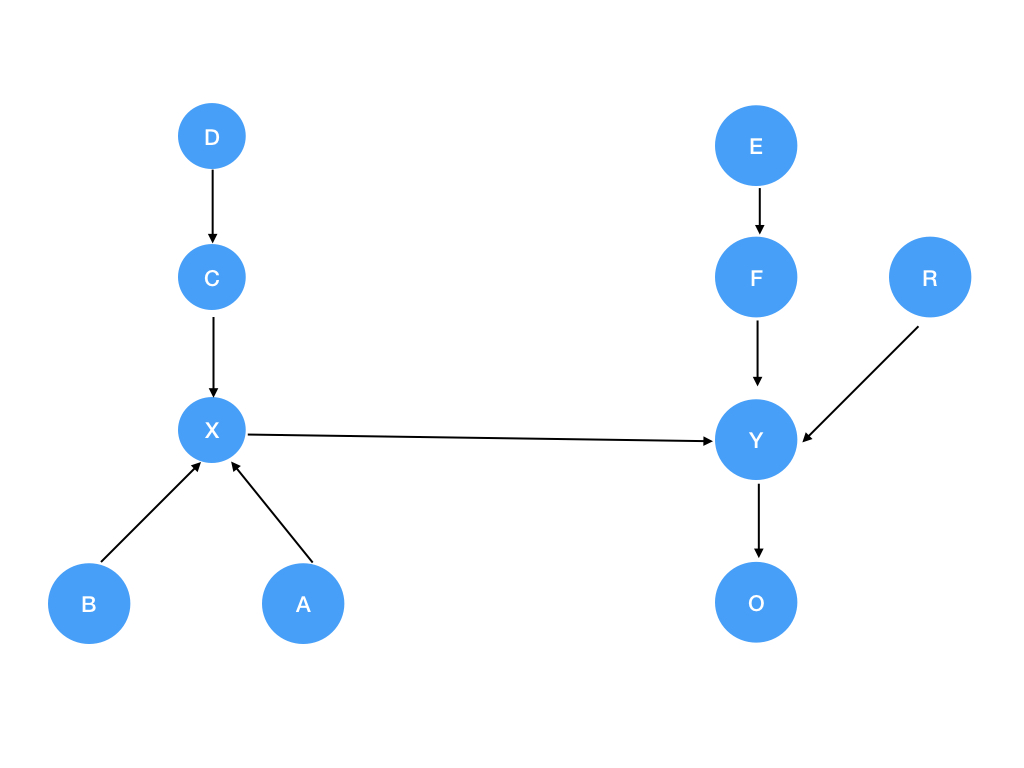
最后再把这个点（从这个点开始访问的）连接到另一个点上，加边就完成了。

枚举边的复杂度为O(n^2)，找环和加边的复杂度为O(n)，所以总的复杂度为O(n^3)。

感谢MZjj帮我debug！

代码：

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <algorithm>
 #include <vector>
 using namespace std;

 const int N = ;
 const int inf = 0x3f3f3f3f;

 struct edge
 {
     int x,y,w;

     edge(){};

     edge(int a,int b,int c)
     {
         x = a;
         y = b;
         w = c;
     }
 };

 vector<edge> es;

 int par[N];
 int n,m;
 int dis[N][N];
 bool vis[N];
 int num;
 int Minedge;
 struct edge minedge;

 bool cmp(edge aa,edge bb)
 {
     return aa.w < bb.w;
 }

 void init(void)
 {
     for (int i = ;i < n;i++) par[i] = i;

     num = ;

     es.clear();

     memset(dis,inf,sizeof(dis));

     Minedge = inf;
 }

 int LCA(int x,int y)
 {
     memset(vis,,sizeof(vis));

     while ()
     {
         vis[x] = ;

         if (x == par[x]) break;

         x = par[x];
     }

     while (!vis[y] && y != par[y])
     {
         y = par[y];
     }

     if (!vis[y]) return -;

     return y;
 }

 void findcycle(int k)
 {
     int x = es[k].x,y = es[k].y;

     int lca = LCA(x,y);

     if (lca == -) return;

     minedge.w = inf;

     while (x != par[x] && x != lca)
     {
         if (dis[x][par[x]] < minedge.w)
         {
             minedge = edge(par[x],x,dis[x][par[x]]);
         }

         x = par[x];
     }

     while (y != par[y] && y != lca)
     {
         if (dis[y][par[y]] < minedge.w)
         {
             minedge = edge(par[y],y,dis[y][par[y]]);
         }

         y = par[y];
     }

     par[minedge.y] = minedge.y;

     Minedge = inf;

     for (int i = ;i < n;i++)
     {
         Minedge = min(dis[par[i]][i],Minedge);
     }

     num--;
 }

 void adde(int k)
 {
     int x = es[k].x,y = es[k].y;

     if (x == par[x]) par[x] = y;
     else if (y == par[y]) par[y] = x;
     else
     {
         vector<int> v;

         while ()
         {
             v.push_back(x);

             if (x == par[x]) break;

             x = par[x];
         }

         for (int i = v.size() - ;i > ;i--) par[v[i]] = v[i-];

         par[es[k].x] = es[k].y;
     }

     num++;

     Minedge = min(Minedge,es[k].w);
 }

 int main()
 {
     while (scanf("%d",&n) && n)
     {
         scanf("%d",&m);

         init();

         for (int i = ;i < m;i++)
         {
             int a,b,c;

             scanf("%d%d%d",&a,&b,&c);

             es.push_back(edge(a,b,c));
         }

         for (int i = ;i < m;i++)
         {
             int x = es[i].x,y = es[i].y;

             dis[x][y] = dis[y][x] = es[i].w;
         }

         sort(es.begin(),es.end(),cmp);

         int ans = inf;

         for (int i = ;i < m;i++)
         {
             findcycle(i);
             adde(i);

             if (num == n - )
             {
                 //cout << es[i].w << " ** " << Minedge << endl;
                 ans = min(ans,es[i].w - Minedge);
             }
         }

         cout << ans << endl;
     }

     return ;
 }