【机器学习】--鲁棒性调优之L1正则，L2正则

一、前述

鲁棒性调优就是让模型有更好的泛化能力和推广力。

二、具体原理

1、背景

第一个更好，因为当把测试集带入到这个模型里去。如果测试集本来是100，带入的时候变成101，则第二个模型结果偏差很大，而第一个模型偏差不是很大。

2、目的

鲁棒性就是为了让w参数也就是模型变小，但不是很小。所以引出了 L1和L2正则。

 L1和L2的使用就是让w参数减小的使用就是让w参数减小。

L1正则，L2正则的出现原因是为了推广模型的泛化能力。相当于一个惩罚系数。

3、具体使用

L1正则：Lasso Regression

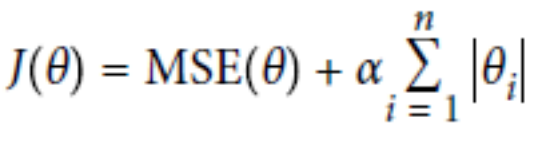
L2正则：Ridge Regression

总结：

经验值 MSE前系数为1 ，L1 , L2正则前面系数一般为0.4~0.5 更看重的是准确性。

L2正则会整体的把w变小。

L1正则会倾向于使得w要么取1，要么取0 ，稀疏矩阵 ，可以达到降维的角度。

ElasticNet函数（把L1正则和L2正则联合一起）：

总结：

1.默认情况下选用L2正则。

2.如若认为少数特征有用，可以用L1正则。

3.如若认为少数特征有用，但特征数大于样本数，则选择ElasticNet函数。

4、在保证正确率的情况下加上正则。

5、如果把lamda设置成0，就只看准确率。

6、如果把lamda设置大些，就看中推广能力。

7、L1倾向于使得w要么取1，要么取0 稀疏编码 可以降维

8、L2倾向于使得w整体偏小 岭回归 首选

 4、图示

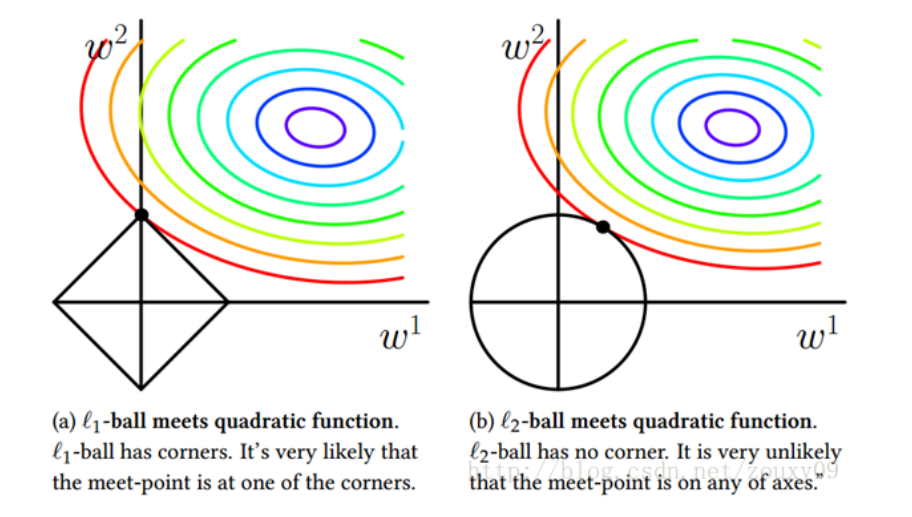
左边是L1正则+基本损失函数

右边是L2正则+基本损失函数

中间部分是圆心，损失函数最小，与正则函数相交，则既要满足基本函数，也要满足L1，L2正则，则损失函数增大了。

w1,w2等等与基本函数相交，则w1,w2都在[0,1]之间。

三、代码演示

代码一：L1正则

# L1正则
import numpy as np
from sklearn.linear_model import Lasso
from sklearn.linear_model import SGDRegressor

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

lasso_reg = Lasso(alpha=0.15)
lasso_reg.fit(X, y)
print(lasso_reg.predict(1.5))

sgd_reg = SGDRegressor(penalty='l1')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

代码二：L2正则

# L2正则
import numpy as np
from sklearn.linear_model import Ridge
from sklearn.linear_model import SGDRegressor

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)

#两种方式第一种岭回归
ridge_reg = Ridge(alpha=1, solver='auto')
ridge_reg.fit(X, y)
print(ridge_reg.predict(1.5))#预测1.5的值
#第二种 使用随机梯度下降中L2正则
sgd_reg = SGDRegressor(penalty='l2')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))

代码三：Elastic_Net函数

# elastic_net函数
import numpy as np
from sklearn.linear_model import ElasticNet
from sklearn.linear_model import SGDRegressor

X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)
#两种方式实现Elastic_net
elastic_net = ElasticNet(alpha=0.1, l1_ratio=0.5)
elastic_net.fit(X, y)
print(elastic_net.predict(1.5))

sgd_reg = SGDRegressor(penalty='elasticnet')
sgd_reg.fit(X, y.ravel())
print(sgd_reg.predict(1.5))