决策树学习笔记（Decision Tree）

　什么是决策树？

　　决策树是一种基本的分类与回归方法。其主要有点事模型具有可得性，分类速度快。学习时，利用训练数据，根据损失函数最小化原则建立决策树模型；预测时，对新数据，利用决策树模型进行分类。

　决策树学习通常包含以下三个步骤：

• 　　选择特征
• 　　决策树生成
• 　　剪枝

　决策树的改进路线：

　　ID3--->C4.5--->CART

　　（1）其中ID3是基于信息增益来选择划分属性

　　（2）C4.5不直接使用增益率来选择划分属性，而是使用了一个启发式：先从候选划分属性中选取信息增益高于平局水平的属性，再从中选择增益率最高的。

　　（3）CART（Classification and Regression Tree）算法使用基尼系数来代替信息增益比。

　信息

　　这个是熵和信息增益的基础概念，是对一个抽象事物的命名，无论用不用‘信息’来命名这种抽象事物，或者用其他名称来命名这种抽象事物，这种抽象事物是客观存在的。如果带分类的事物集合可以划分为多个类别当中，则某个类（xi）的信息（量）定义如下：

　        

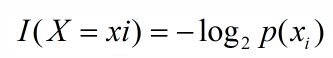
　　I(x)用来表示随机变量的信息，p(xi)指是当xi发生时的概率。当事件xi发生的概率p(xi)很小，但是它却发生了，那这个信息量相当大，比如买彩票中奖了，那么这个信息量肯定是很大的。相反，对于大概率事件，人们习以为常，那么这个事件的信息量就很小。这就体现在上述公式中。

　信息熵

　　“信息熵”是度量样本纯度最常用的一种指标。所谓样本纯度，相反而言之就是凌乱程度。如一个数据集U中的样本都属于同一类，那么这时样本纯度最高而凌乱程度最低。信息熵定义为：

　　　

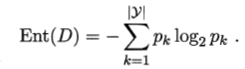
　　其中D表示样本集合，|y|样本中类别的数目， pk表示第k种分类占集合的比例。Ent(D)的值越小，D的纯度越高。

　信息增益

　　信息增益 指的是，使用某一个属性a进行划分后，所带来的纯度提高的大小。一般而言，信息增益越大，意味着使用属性a来进行划分所获得的“纯度提升”越大。信息增益定义如下：　　

　　　　

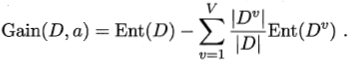
　　即

　　信息增益 = 根节点的信息熵 - 所有分支节点的信息熵的加权和

　　其中，权值为划分后属性a=ak节点中样本的数量与划分前节点中的样本数量的比值，即概率。概率确保了权重的和为1.

　　　　　　　　

　　　　　　上图描述的是，使用属性a对样本集合D进行划分，因为a有V个取值，因此决策树会有V个分支。划分后每一个节点中样本的数量为属性a=ak的样本的数量。

　　　　问：如何理解：信息增益越大，意味着使用属性a来进行划分所获得的“纯度提升”越大?

　　　　答：因为Ent(D)的值越小，D的纯度越高。而划分后，所有的分支节点的Ent(Dk)的和就是划分后的信息熵，公式体现了前后的差距，如果差距越大，那么就说明划分后所有的分支节点的信息熵越小，纯度提升越大。

　增益率

　　背景：当样本集中的某一属性取值使得所有样本被分到不同类别，此时分支的纯度达到最高，无需再继续划分。然而这样的决策树不具备泛化能力。事实上，信息增益准则对可取值较多的属性有所偏好。

　　为了减少这种偏好可能带来的影响，因此使用增益率代替信息增益准则选择划分属性。

　　即增益率(Gain_ratio(D,a))=信息增益Gain(D,a)/属性固有值(IV(a))。
　　属性A的可能取值越大，固有值IV(a)通常越大。
　　信息增益率偏向于可能取值减少的属性。因此C4.5算法不直接使用信息增益率来选择划分属性。

　基尼值

　　基尼值 Gini(D) 反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。当数据集的纯度越高，每次抽到不同类别标记的概率越小。打个比方，在一个袋子里装100个乒乓球，其中有99个白球，1个黄球，那么当我们随机抽取两个球的时候，很大概率是抽到两个白球。

　　所以数据集D的纯度可以用基尼值类度量，其定义如下：

　　　　

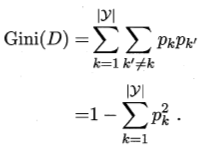
　　基尼值越小，数据集D纯度越高。

　基尼指数

　　基尼指数是针对于属性定义的，其反映的是，使用属性a进行划分后，所有分支中（使用基尼值度量的）纯度的加权和。

　　属性a的基尼指数定义如下：

　　　

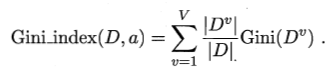
　　我们在属性集合A中选择划分属性的时候，就选择使得划分后基尼指数最小的属性作为最优划分属性。CART就是用基尼指数来选择划分属性的。

　决策树的剪枝处理

　　剪枝是决策树学习算法解决过拟合的主要手段。在决策树的学习过程中，为了尽可能地正确分类训练样本，节点划分得不断重复，有时候会造成决策树的分支过多，，这时候就是算法在训练样本上学得太好，导致把训练集本身的一些特点作为所有数据所有数据都有的一般性质（实际上新数据中可能没有这些特点），从而导致过拟合。因此可以主动去掉一些分支来降低过拟合的风险。

　　决策树的剪枝分为  预剪枝  和  后剪枝 。