coursera-斯坦福-机器学习-吴恩达-笔记week2
1 多元线性回归
1.1 假设函数
多元线性回归是指有多个特征特征变量的情况。此时我们修改假设函数hθ(x)=θ0+θ1∗x为hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn。
设x0=1,x为特征向量,θ为参数向量,则hθ(x)=θTx。
1.2 cost function与梯度下降
cost函数依然选择平方误差函数
梯度下降方法也没有变:

1.3 特征约简
当变量的范围差别很大时,梯度下降法就会收敛的很慢,此时我们使输入的变量大致属于相同的范围来加速梯度下降。
两种方法:特征缩放、均值归一化(x-μi)/最大值
1.4 多项式回归
有时候曲线能更好的拟合数据,这时可以采用多项式回归。
假设函数为: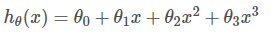
设x2=x12,x3=x13。则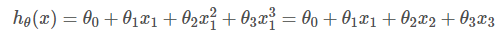 。
。
这样就把多项式回归转变成了多参数线性回归。
2 正规方程
1. 梯度下降要设置α并不保证一次能获得最优的α,正规方程不用考虑α。
2. 梯度下降要迭代多次,正规方程不用。(所以,遇到比较简单的情况,可用正规方程)
3. 梯度下降最后总能得到一个最优结果,正规方程不一定。因为正规方程要求X的转置乘X的结果可逆。
4. 当特征数量很多的时候,正规方程计算不方便,不如梯度下降。
3 Octave 基础教程
4 编程作业——实现线性回归
代码和解释详见 https://blog.csdn.net/Cowry5/article/details/80174130。
实验结果: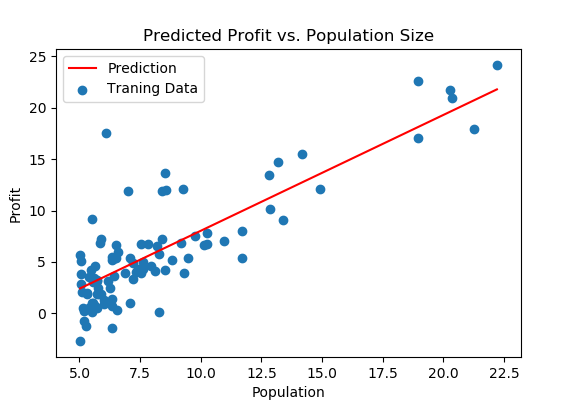

coursera-斯坦福-机器学习-吴恩达-笔记week2的更多相关文章
- coursera-斯坦福-机器学习-吴恩达-笔记week1
1 Introduction 1.1 概念:一个程序被认为能从经验E中学习,解决任务 T,达到性能度量值P,当且仅当, 有了经验E后,经过P评判, 程序在处理 T 时的性能有所提升. 1.2 机器学习 ...
- coursera-斯坦福-机器学习-吴恩达-笔记week4
1 神经网络的提出 线性回归和逻辑回归能很好的解决特征变量较少的问题,但对于变量数量增加的复杂非线性问题,单纯增加二次项和三次项等特征项的方法计算代价太高. 2 神经网络算法 2.1 神经元 模拟神经 ...
- coursera-斯坦福-机器学习-吴恩达-笔记week3
1 逻辑回归 1. classification 分类 eg:垃圾邮件分类.交易是否是欺诈.肿瘤类别.分类的结果是离散值. 2. sigmoid函数 使用线性方法来判断分类问题,会出现上图中的问题,需 ...
- 第19月第8天 斯坦福大学公开课机器学习 (吴恩达 Andrew Ng)
1.斯坦福大学公开课机器学习 (吴恩达 Andrew Ng) http://open.163.com/special/opencourse/machinelearning.html 笔记 http:/ ...
- 吴恩达《机器学习》课程笔记——第六章:Matlab/Octave教程
上一篇 ※※※※※※※※ [回到目录] ※※※※※※※※ 下一篇 这一章的内容比较简单,主要是MATLAB的一些基础教程,如果之前没有学过matlab建议直接找一本相关书籍,边做边学,matl ...
- 笔记:《机器学习训练秘籍》——吴恩达deeplearningai微信公众号推送文章
说明 该文为笔者在微信公众号:吴恩达deeplearningai 所推送<机器学习训练秘籍>系列文章的学习笔记,公众号二维码如下,1到15课课程链接点这里 该系列文章主要是吴恩达先生在机器 ...
- 吴恩达(Andrew Ng)——机器学习笔记1
之前经学长推荐,开始在B站上看Andrew Ng的机器学习课程.其实已经看了1/3了吧,今天把学习笔记补上吧. 吴恩达老师的Machine learning课程共有113节(B站上的版本https:/ ...
- ML:吴恩达 机器学习 课程笔记(Week1~2)
吴恩达(Andrew Ng)机器学习课程:课程主页 由于博客编辑器有些不顺手,所有的课程笔记将全部以手写照片形式上传.有机会将在之后上传课程中各个ML算法实现的Octave版本. Linear Reg ...
- Coursera课程《Machine Learning》吴恩达课堂笔记
强烈安利吴恩达老师的<Machine Learning>课程,讲得非常好懂,基本上算是无基础就可以学习的课程. 课程地址 强烈建议在线学习,而不是把视频下载下来看.视频中间可能会有一些问题 ...
随机推荐
- Linux下安装jieba
Jieba代码对 Python 2/3 均兼容 * 全自动安装:`easy_install jieba` 或者 `pip install jieba` / `pip3 install jieba` * ...
- 栈ADT
栈 栈是限制插入和删除只能在同一位置的表,这一位置称为栈顶(top),也可能称为LIFO表 对于空栈的pop(弹栈)操作是一个ADT错误,但是若是push(压栈)时空间超限并不是ADT错误 实现:基于 ...
- c# 结构的使用
类的定义的是引用类型,重点在堆上创建,有的时候类只包含极少的数据,因为管理堆而造成的开销是很大的.这时候更好的做法就是将类型定义成结构.结构是值类型,在栈上存储,能有效的减小内存管理的开销.c#基元类 ...
- oracle(2)
create table aaa( id number, name varchar2(100) ); select decode((select max(id) from aaa),null,'x', ...
- Linux(5.5版为主)的基本操作命令
mount 查看挂载目录 cat ~ 查看文件下的内容 touch ~ 创建一个文件 一次性性创建几个文件: touch /tmp/{1,2,3,4}.txt ...
- 用Java画简单验证码
以下是具体代码: package com.jinzhi.tes2; import java.awt.Color;import java.awt.Font;import java.awt.Graphic ...
- hashmap相关面试题
- Python select实现socket并发
Python select Python的select()方法直接调用操作系统的IO接口,它监控sockets,open files, and pipes(所有带fileno()方法的文件句柄)何时 ...
- ★Pandas 零碎知识
1 修改属性 1.1 修改1列的类型属性: df['总金额'] = pd.to_numeric(df['总金额']) #转变dataframe的1列为数值型 1.2 多列设为数值型:(使用DataFr ...
- Python3 tkinter基础 Menu add_cascade 多级菜单 add_separator 分割线
Python : 3.7.0 OS : Ubuntu 18.04.1 LTS IDE : PyCharm 2018.2.4 Conda ...
