【POJ1187】陨石的秘密

题目大意：

定义一个串：只含有 '( )'，'[ ]'，'{ }'，3种（6个）字符。

定义 SS 串：

1. 空串是SS表达式。
2. 若A是SS表达式，且A串中不含有中括号和大括号，则(A)是SS表达式。
3. 若A是SS表达式，且A串中不含有大括号，则[A]是SS表达式。
4. 若A是SS表达式，则{A}是SS表达式。
   
   定义SS串深度：
5. 空串深度为0.
6. 若A可以写成*A'*，其中A‘为SS串，*为任意括号，则\(D(A)=D(A’)+1\)。
7. 若A可以写成BC的形式，其中B、C均是SS串，则\(D(A)=max\{D(B),D(C) \}\)。
   
   求由l1个对括号，l2对中括号，l3对大括号，深度为d 构成的SS串的个数。

题解：这是一道字符串上的计数类 dp 问题，一般对于字符串计数类问题都先把字符串划分成若干个独立的部分，即：划分子问题，再进行求解。首先是状态的选择，\(dp[d][i][j][k]\) 表示深度不超过 d，且由 i，j，k 个对应括号构成的SS串的个数，之所以选择深度不超过 d，是因为若选择深度恰好为 d，将很难从子状态转移到当前状态，或者说，要考虑的情况也比较多。转移到状态转移如下：



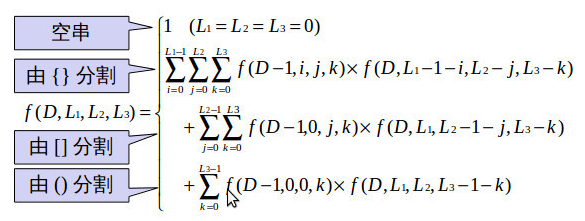
在看题解时，看到了另一种比较优秀的解释：对于每一个括号序列可以看成是一棵树的 dfs 序列（类似 dfs 序），树的最大深度是 d，求计数。

记忆化搜搜版代码如下

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <memory.h>
using namespace std;
const int mod=11380;

int dp[31][11][11][11],l1,l2,l3,d;

int dfs(int dep,int x,int y,int z){
	int &ans=dp[dep][x][y][z];
	if(dep<0)return 0;
	if(!dep){
		if(x+y+z==0)return 1;
		else return 0;
	}
	if(x+y+z==0)return 1;
	if(ans>=0)return ans;
	int cnt=0;
	for(int i=0;i<x;i++)
		for(int j=0;j<=y;j++)
			for(int k=0;k<=z;k++)
				cnt=(cnt+(long long)dfs(dep-1,i,j,k)*dfs(dep,x-1-i,y-j,z-k))%mod;
	for(int j=0;j<y;j++)
		for(int k=0;k<=z;k++)
			cnt=(cnt+(long long)dfs(dep-1,0,j,k)*dfs(dep,x,y-1-j,z-k))%mod;
	for(int k=0;k<z;k++)cnt=(cnt+(long long)dfs(dep-1,0,0,k)*dfs(dep,x,y,z-1-k))%mod;
	return ans=cnt;
}

int main(){
	scanf("%d%d%d%d",&l1,&l2,&l3,&d);
	memset(dp,-1,sizeof(dp));
	printf("%d\n",(dfs(d,l1,l2,l3)-dfs(d-1,l1,l2,l3)+mod)%mod);
	return 0;
}

迭代版代码如下

#include <cmath>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;

const int P = 11380;
const int M = 35;
const int N = 15;
int f[N][N][N][M];

int fun(int a, int b, int c, int d) {
    if (a + b + c == 0) return 1;
    int tmp = 0;
    for (int i = 0; i < c; i++)
        tmp = (tmp + f[a][b][c - i - 1][d] * f[0][0][i][d - 1]) % P;
    for (int i = 0; i < b; i++)
        for (int j = 0; j <= c; j++)
            tmp = (tmp + f[a][b - i - 1][c - j][d] * f[0][i][j][d - 1]) % P;
    for (int i = 0; i < a; i++)
        for (int j = 0; j <= b; j++)
            for (int k = 0; k <= c; k++)
                tmp = (tmp + f[a - i - 1][b - j][c - k][d] * f[i][j][k][d - 1]) % P;
    return tmp;
}

int main() {
    int l1, l2, l3, d;
    cin >> l1 >> l2 >> l3 >> d;
    f[0][0][0][0] = 1;
    for (int i = 0; i <= l1; i++)
        for (int j = 0; j <= l2; j++)
            for (int k = 0; k <= l3; k++)
                for (int l = 1; l <= d; l++)
                    f[i][j][k][l] = fun(i, j, k, l);
    if (d) f[l1][l2][l3][d] = (f[l1][l2][l3][d] - f[l1][l2][l3][d - 1] + P) % P;
    cout << f[l1][l2][l3][d] << endl;
    return 0;
}