算法实践--最小生成树(Kruskal算法)

什么是最小生成树(Minimum Spanning Tree)

每两个端点之间的边都有一个权重值，最小生成树是这些边的一个子集。这些边可以将所有端点连到一起，且总的权重最小

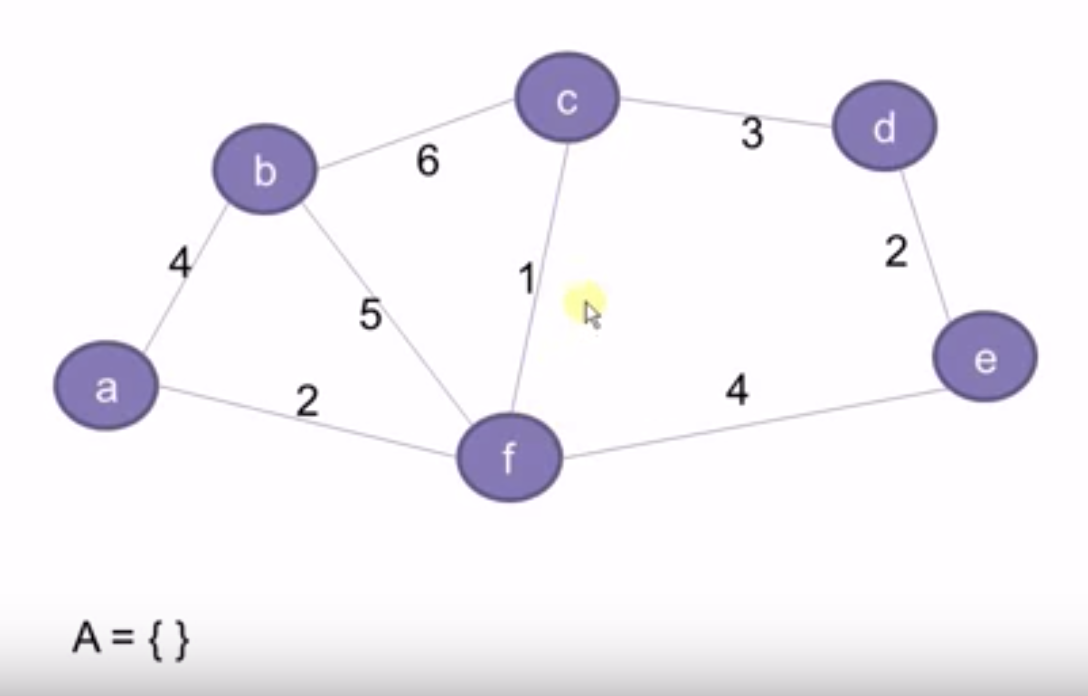
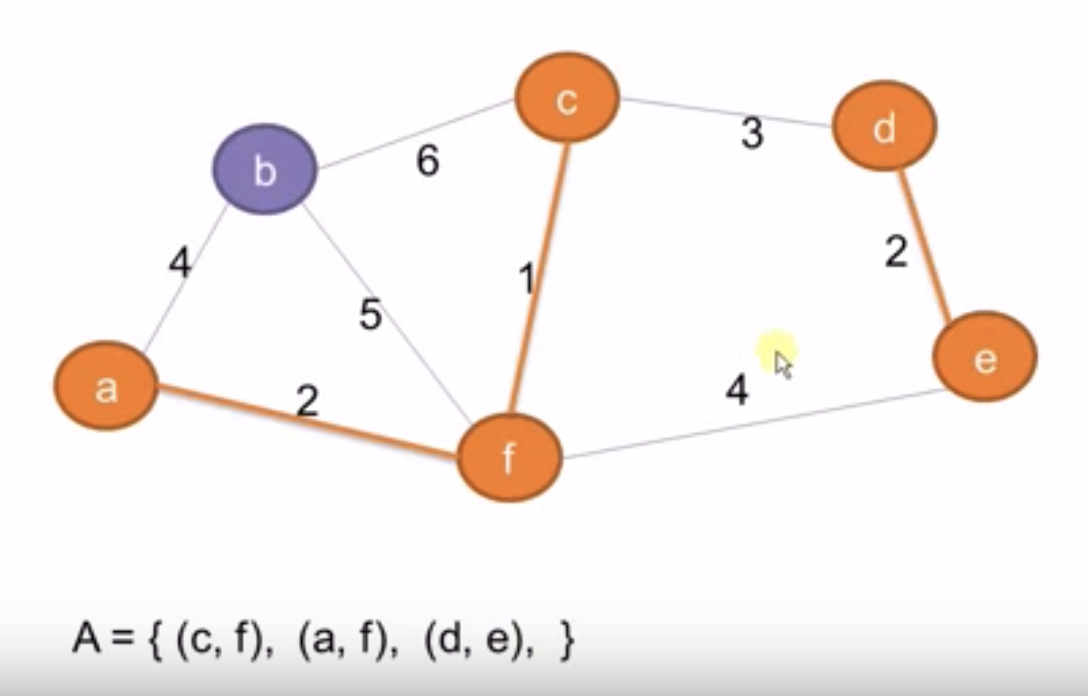
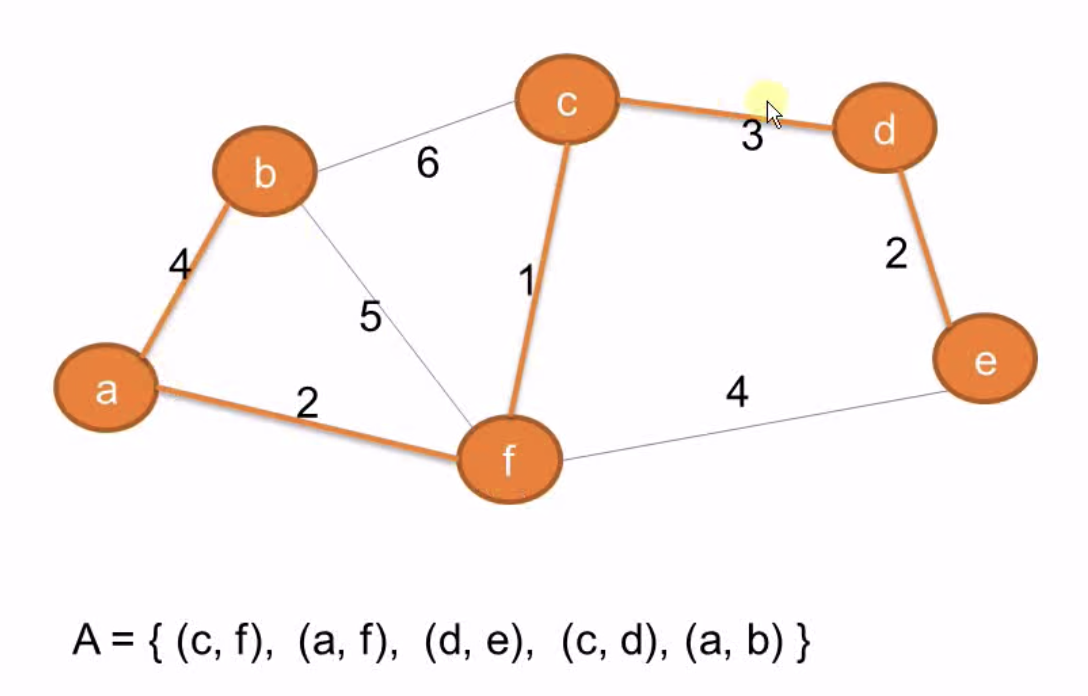
下图所示的例子，最小生成树是{cf, fa, ab} 3条边

Kruskal算法

用到上一篇中介绍的不相交集合(并查集)

首先，定义V是端点的集合，E是边的集合，A为要求的最小生成树集合

• 初始A为空集合，每个端点都作为单独的不相交集合
• 将所有边根据其权重进行排序
• 对每条边(v1, v2)，如果其两个端点数据不同的不相交集，则将该边加到集合A中，同时将v1和v2合并
• 最终得到的A即为最小生成树

生成过程的示例图

C++代码示例

struct Edge {
    char vertex1;
    char vertex2;
    int weight;
    Edge(char v1, char v2, int w):vertex1(v1), vertex2(v2), weight(w) {}
};

struct Graph {
    vector<char> vertice;
    vector<Edge> edges;
};

unordered_map<char, char> PARENT;
unordered_map<char, int> RANK;

char find(char vertex) {
    if (PARENT[vertex] == vertex)
        return PARENT[vertex];
    else
        return find(PARENT[vertex]);
}

void MST(Graph& g) {
    vector<Edge> res;

    for (auto c : g.vertice) {
        PARENT[c] = c;
        RANK[c] = ;
    }

    sort(g.edges.begin(), g.edges.end(), [](Edge x, Edge y) {return x.weight < y.weight;});   // O(E*log(E))

    for (Edge e : g.edges) {         // O(E)
        char root1 = find(e.vertex1);  // 最差O(E)，因为有记录深度，Find可以认为很快
        char root2 = find(e.vertex2);
        if (root1 != root2) {
            res.push_back(e);
            if (RANK[root1] > RANK[root2]) {
                PARENT[root2] = root1;
                RANK[root1]++;
            } else {
                PARENT[root1] = root2;
                RANK[root2]++;
            }
        }
    }

    for (Edge e : res) {
        cout << e.vertex1 << " -- " << e.vertex2 << "  " << e.weight << endl;
    }
}

void Union( char vertex_1, char vertex_2 ) {
}

int main() {

    char t[] = {'a', 'b', 'c', 'd', 'e', 'f'};

    Graph g;
    g.vertice = vector<char>(t, t + sizeof(t)/sizeof(t[]));

    g.edges.push_back(Edge('a', 'b', ));  // 稀疏图用链来表示(E = O(V))
    g.edges.push_back(Edge('a', 'f', ));  // 如果是密集图(E = O(V*V)), 用矩阵来表示
    g.edges.push_back(Edge('f', 'b', ));  // 大部分感兴趣的图是稀疏的
    g.edges.push_back(Edge('c', 'b', ));
    g.edges.push_back(Edge('c', 'f', ));
    g.edges.push_back(Edge('f', 'e', ));
    g.edges.push_back(Edge('d', 'e', ));
    g.edges.push_back(Edge('d', 'c', ));

    MST(g);

    return ;
}