CF(438D) The Child and Sequence(线段树)

题意：对数列有三种操作：

1. Print operation l, r. Picks should write down the value of .
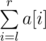2. Modulo operation l, r, x. Picks should perform assignment a[i] = a[i] mod x for
   each i (l ≤ i ≤ r).
3. Set operation k, x. Picks should set the value of a[k] to x (in
   other words perform an assignment a[k] = x).

解法：线段树更新。维护区间最大值ma和区间sum。假设訪问的x小于ma就能够忽略。否则向下更新；

代码：  

/******************************************************
* author:xiefubao
*******************************************************/
#pragma comment(linker, "/STACK:102400000,102400000")
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
#include <cmath>
#include <map>
#include <set>
#include <stack>
#include <string.h>
//freopen ("in.txt" , "r" , stdin);
using namespace std;

#define eps 1e-8
const double pi=acos(-1.0);
typedef long long LL;
const int Max=100100*2;
const int INF=1000000007;
struct node
{
    int l,r;
    node * left,*right;
    int ma;
    LL sum;
} nodes[Max];
int Mid(node* p)
{
    return (p->l+p->r)/2;
}
int tot=0;
void buildtree(node* p,int left,int right)
{
    p->l=left;
    p->r=right;
    p->ma=0;
    p->sum=0;
    if(left==right)
        return ;
    int mid=(left+right)/2;
    tot++;
    p->left=nodes+tot;
    buildtree(p->left,left,mid);
    tot++;
    p->right=nodes+tot;
    buildtree(p->right,mid+1,right);
}
void update(node* p,int i,int value)
{
    if(p->l==i&&p->r==i)
    {
        p->sum=value;
        p->ma=value;
        return ;
    }
    int mid=Mid(p);
    if(i<=mid)
        update(p->left,i,value);
    else
        update(p->right,i,value);
    p->sum=p->left->sum+p->right->sum;
    p->ma=max(p->left->ma,p->right->ma);
}
void update2(node* p,int l,int r,int x)
{
    if(p->ma<x)
        return;
    if(p->l==l&&p->r==r&&l==r)
    {
        p->sum%=x;
        p->ma=p->sum;
        return ;
    }
    int mid=Mid(p);
    if(r<=mid)
        update2(p->left,l,r,x);
    else if(l>mid)
        update2(p->right,l,r,x);
    else
    {
        update2(p->left,l,mid,x);
        update2(p->right,mid+1,r,x);
    }
    p->sum=p->left->sum+p->right->sum;
    p->ma=max(p->left->ma,p->right->ma);
}
LL query(node* p,int l,int r)
{
    if(l==p->l&&r==p->r)
    {
        return p->sum;
    }
    int mid=Mid(p);
    if(r<=mid)
        return query(p->left,l,r);
    if(l>mid)
        return query(p->right,l,r);
    return query(p->left,l,mid)+query(p->right,mid+1,r);;
}
int n,m;
int main()
{
    while(scanf("%d%d",&n,&m)==2)
    {
        tot=0;
        buildtree(nodes,0,n+1);
        for(int i=1; i<=n; i++)
        {
            int a;
            scanf("%d",&a);
            update(nodes,i,a);
        }
        while(m--)
        {
            int t;
            scanf("%d",&t);
            if(t==1)
            {
                int l,r;
                scanf("%d%d",&l,&r);
                cout<<query(nodes,l,r)<<endl;
            }
            else if(t==2)
            {
                int l,r,x;
                scanf("%d%d%d",&l,&r,&x);
                update2(nodes,l,r,x);
            }
            else if(t==3)
            {
                int i,x;
                scanf("%d%d",&i,&x);
                update(nodes,i,x);
            }
        }
    }
    return 0;
}