【Computer Vision】图像单应性变换/投影/仿射/透视

一、基础概念

1. projective transformation  = homography = collineation.

2. 齐次坐标：使用N+1维坐标来表示N维坐标，例如在2D笛卡尔坐标系中加上额外变量w来形成2D齐次坐标系$(x,y) \Rightarrow (x,y,w)$

齐次坐标具有规模不变性，同一点可以被无数个齐次坐标表达.$(x,y,1) \Rightarrow (ax,ay,a)$ 齐次坐标转化为笛卡尔坐标可以通过同除最后一项得到.

3. 单应性变换是对齐次坐标下点的线性变换，可以通过矩阵运算来表达$ x^{'}= Hx$

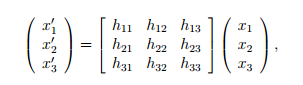
H为非奇异矩阵.

二、基础变换

刚体变换(rigid transformation): 旋转和平移变换/rotation,translation, 3个自由度，点与点之间的距离不变
$$ x' = \begin{pmatrix} R&t \\ 0^T&1\end{pmatrix}x $$

R为2*2旋转矩阵，t为2维列向量，0^T为0的二维行向量

相似变换(similarity transformation): 增加了缩放尺度, 四个自由度，点与点之间的距离比不变

$$x' = \begin{pmatrix} sR & t  \\  0^T & 1 \end{pmatrix}x$$

s为缩放尺度

仿射变换(affine transformation): 仿射变换和相似变换近似，不同之处在于相似变换具有单一旋转因子和单一缩放因子，仿射变换具有两个旋转因子和两个缩放因子，因此具有6个自由度. 不具有保角性和保持距离比的性质，但是原图平行线变换后仍然是平行线.

$$x' = \begin{pmatrix}A&t \\ 0^T&1\end{pmatrix}x$$

A为2*2的非奇异矩阵,可被分解为如下: $A = R(\theta)R(-\phi)DR(\phi)$

其中$R(\theta) R(\phi)$ 为旋转矩阵，D为对角阵$ D = \begin{pmatrix} \lambda_1 & 0 \\ 0 & \lambda_2 \end{pmatrix} $

$\lambda_1 和 \lambda_2$可以看做两个方向的缩放比.

投影变换(projective transformation): 也叫作单应性变换。投影变换是齐次坐标下非奇异的线性变换。然而在非齐次坐标系下却是非线性的，这说明齐次坐标的发明是很有价值的。投影变换比仿射变换多2个自由度，具有8个自由度。上面提到的仿射变换具有的“不变”性质，在投影变换中已不复存在了。尽管如此，它还是有一项不变性，那就是在原图中保持共线的3个点，变换后仍旧共线。投影变换表示如下：

$$x' = \begin{pmatrix}A&t \\ V^T&v\end{pmatrix}x$$

其中$V = (v_1,v_2)^T$

透视变换: 透视变换将图像投影到一个新的视平面，是二维到三维再到另一个二维(x', y')空间的映射。

透视变换前两行和仿射变换相同，第三行用于实现透视变换。透视变换前后，原来共线的三个点，变换之后仍然共线。

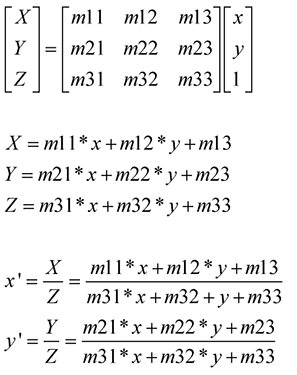
以上公式设变换之前的点是z值为1的点，它三维平面上的值是x,y,1，在二维平面上的投影是x,y，通过矩阵变换成三维中的点X,Y,Z，再通过除以三维中Ｚ轴的值，转换成二维中的点x’,y’.
从以上公式可知，仿射变换是透视变换的一种特殊情况．它把二维转到三维，变换后，再转映射回之前的二维空间（而不是另一个二维空间）

三、Python实现

python版本:2.7

依赖包：scipy,numpy,pylab,PIL

1. 使用仿射矩阵进行image warping: 图像扭曲

图片:trees_001.jpg

from scipy import ndimage
from numpy import *
from PIL import Image
from pylab import *
im = array(Image.open('trees_001.jpg').convert('L'))
H = array([[1.4,0.05,-100],[0.05,1.5,-100],[0,0,1]])
#im2  = ndimage.affine_transform(im,H[:2,:2],(H[0,2],H[1,2]))
im2  = ndimage.affine_transform(im,H[:2,:2],(H[0,2],H[1,2]))
figure()
gray()
imshow(im2)
show()

结果: