[poj3565] Ants (二分图带权匹配)

Description

年轻自然主义者比尔在学校研究蚂蚁。他的蚂蚁以苹果树上苹果为食。每个蚁群都需要自己的苹果树来养活自己。

比尔有一张坐标为 n 个蚁群和 n 棵苹果树的地图。他知道蚂蚁会从他们的巢穴到达他们的喂食地点，并使用化学标记的路线返回。这些路线不能相互交叉，不然蚂蚁会感到困惑，并进入错误的巢穴或苹果树，从而引起蚁群之间的战争。

比尔希望将每个蚁群连接到一棵苹果树上，这样所有n个路径都是非相交的直线。在这个问题中，这样的连接方式总是存在的。你的任务是编写一个找到这样的连接方式的程序。

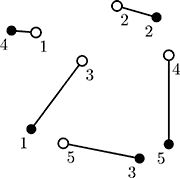
在这张照片上，蚁群用空心圆圈表示，苹果树用实心圆圈表示。这是一条可能的连接方法示意。

Input

输入文件的第一行包含一个整数 n （1≤n≤100 ） - 蚁群和苹果树的数量。之后是描述n个蚁群的n行，之后是描述n棵苹果树的n行。每个蚁群和苹果树由笛卡尔平面上的一对整数坐标 x 和 y （−10000≤x,y≤10000 ）描述。所有蚂蚁巢穴和苹果树在地图上占据不同的点。没有三点是在同一条线上。

Output

输出n行，每行有一个整数。写在第i行上的数字表示连接到第i个蚁群的苹果树的编号（从1到n）。

Sample Input

5

-42 58

44 86

7 28

99 34

-13 -59

-47 -44

86 74

68 -75

-68 60

99 -60

Sample Output

4

2

1

5

3

Solution

Km模板

Code

//By Menteur_Hxy
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
#define F(i,a,b) for(register int i=(a);i<=(b);i++)
using namespace std;
int read() {
	int x=0,f=1; char c=getchar();
	while(!isdigit(c)) {if(c=='-')f=-f;c=getchar();}
	while(isdigit(c)) x=(x<<1)+(x<<3)+c-48,c=getchar();
	return x*f;
}
const int N=128,INF=0x3f3f3f3f;
int n;
int mat[N],va[N],vb[N];
double tmp;
double la[N],lb[N],dis[N][N];
struct Poi{double x,y;}T[N],A[N];
bool dfs(int u) {
	va[u]=1;
	F(v,1,n) if(!vb[v])
		if(la[u]+lb[v]-dis[u][v]<1e-6) {
			vb[v]=1;
			if(!mat[v] || dfs(mat[v])) {mat[v]=u;return 1;}
		}
	return 0;
}
void KM() {
	F(i,1,n) {
		la[i]=-INF,mat[i]=lb[i]=0;
		F(j,1,n) la[i]=max(la[i],dis[i][j]);
	}
	F(i,1,n) {
		while(1) {
			memset(va,0,sizeof(va));
			memset(vb,0,sizeof(vb));
			// cout<<i<<endl;
			if(dfs(i)) break;
			tmp=INF;
			F(j,1,n) if(va[j]) F(k,1,n) if(!vb[k])
				tmp=min(tmp,la[j]+lb[k]-dis[j][k]);
			// cout<<tmp<<endl;
			// F(j,1,n) cout<<la[j]<<" ";cout<<endl;
			// F(j,1,n) cout<<lb[j]<<" ";cout<<endl;
			F(j,1,n) {
				if(va[j]) la[j]-=tmp;
				if(vb[j]) lb[j]+=tmp;
			}
		}
	}
}
int main() {
	// freopen("read.txt","r",stdin);
	// freopen("1.txt","w",stdout);
	while(~scanf("%d",&n)) {
		F(i,1,n) T[i].x=read(),T[i].y=read();
		F(i,1,n) A[i].x=read(),A[i].y=read();
		F(i,1,n) F(j,1,n) dis[i][j]=-sqrt((A[i].x-T[j].x)*(A[i].x-T[j].x)+(A[i].y-T[j].y)*(A[i].y-T[j].y));
		KM();
		F(i,1,n) printf("%d\n",mat[i]);
	}
	return 0;
}