P1233 木棍加工

P1233 木棍加工

题目描述

一堆木头棍子共有n根，每根棍子的长度和宽度都是已知的。棍子可以被一台机器一个接一个地加工。机器处理一根棍子之前需要准备时间。准备时间是这样定义的：

第一根棍子的准备时间为1分钟；

如果刚处理完长度为L，宽度为W的棍子，那么如果下一个棍子长度为Li，宽度为Wi，并且满足L>＝Li，W>＝Wi，这个棍子就不需要准备时间，否则需要1分钟的准备时间；

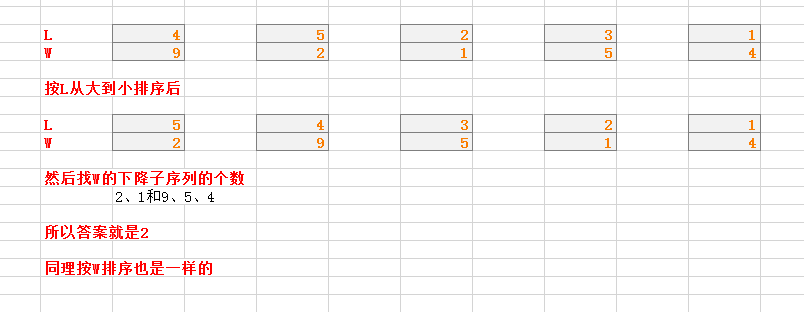
计算处理完n根棍子所需要的最短准备时间。比如，你有5根棍子，长度和宽度分别为(4, 9)，(5, 2)，(2, 1)，(3, 5)，(1, 4)，最短准备时间为2（按(4, 9)、(3, 5)、(1, 4)、(5, 2)、(2, 1)的次序进行加工）。

输入输出格式

输入格式：

第一行是一个整数n(n<＝5000)，第2行是2n个整数，分别是L1，W1，L2，w2，…，Ln，Wn。L和W的值均不超过10000，相邻两数之间用空格分开。

输出格式：

仅一行，一个整数，所需要的最短准备时间。

输入输出样例

输入样例#1：

5
4 9 5 2 2 1 3 5 1 4

输出样例#1：

2

 

 

分析：

 

 

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cstdlib>
 using namespace std;
 int n;
 struct node{
     int x,y;
 }s[];
 int f[];
 int maxn=;
 bool cmp(node a,node b)
 {
     return a.x>b.x;
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<=n;i++) scanf("%d%d",&s[i].x,&s[i].y);
     sort(s+,s+n+,cmp);
     for(int i=;i<=n;i++) f[i]=;
     for(int i=;i<=n;i++)
      for(int j=;j<i;j++)
       if(s[i].y>s[j].y) f[i]=max(f[i],f[j]+),maxn=max(maxn,f[i]);
     printf("%d",maxn);
     return ;
 }