线性回归模型(Linear Regression)及Python实现
线性回归模型(Linear Regression)及Python实现
1.模型
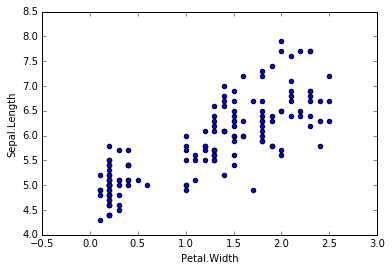
对于一份数据,它有两个变量,分别是Petal.Width和Sepal.Length,画出它们的散点图。我们希望可以构建一个函数去预测Sepal.Length,当我们输入Petal.Width时,可以返回一个预测的Sepal.Length。从散点图可以发现,可以用一条直线去拟合,这时我们可以构建一元线性回归模型:hθ(x) = θ0 + θ1x1 (x1= Petal.Width)。当然,如果我们的特征X不止一个的话,我们可以构造多元线性回归模型,hθ(x) = ∑θixi (i = 0,...,n , x0 = 1)。
2.评价
对于上述的线性回归模型hθ(x),我们需要求出θ来。可以想象,参数θ的取值有无数多种,那么我们应该怎么样选取合适的参数θ? 直观的去理解,我们希望估计出来的hθ(x)与实际的Y值尽量的靠近,因此我们可以定义一个损失函数J(θ) = (1/2m)∑(hθ(x(i)) − y(i))2,m为样本量。当然,损失函数可以有很多种定义方法,这种损失函数是最为经典的,由此得到的线性回归模型称为普通最小二乘回归模型(OLS)。
3.优化
我们已经定义好了损失函数J(θ),接下来的任务就是求出参数θ。我们的目标很明确,就是找到一组θ,使得我们的损失函数J(θ)最小。最常用的求解方法有两种:批量梯度下降法(batch gradient descent), 正规方程方法(normal equations)。 前者是一种通过迭代求得的数值解,后者是一种通过的公式一步到位求得的解析解。在特征个数不太多的情况下,后者的速度较快,一旦特征的个数成千上万的时候,前者的速度较快。另外,先对特征标准化可以加快求解速度。
批量梯度下降法:θj := θj − α· ∂J(θ)/∂θj (j = 0,1,...,n, α为学习速率, J(θ)/∂θj 为J的偏导数) 不断同时更新θj直到收敛
正规方程法:θ = (XTX)−1XTY
4.python代码实现
# -*- coding: utf-8 -*-
"""
Created on Tue Feb 23 16:06:54 2016 @author: SumaiWong
""" import numpy as np
import pandas as pd
from numpy.linalg import inv
from numpy import dot iris = pd.read_csv('iris.csv')
# 拟合线性模型: Sepal.Length ~ Sepal.Width + Petal.Length + Petal.Width # 正规方程法
temp = iris.iloc[:, 1:4]
temp['x0'] = 1
X = temp.iloc[:,[3,0,1,2]]
Y = iris.iloc[:, 0]
Y = Y.reshape(len(iris), 1)
theta_n = dot(dot(inv(dot(X.T, X)), X.T), Y) # theta = (X'X)^(-1)X'Y
print theta_n #批量梯度下降法
theta_g = np.array([1., 1., 1., 1.]) #初始化theta
theta_g = theta_g.reshape(4, 1)
alpha = 0.1
temp = theta_g
X0 = X.iloc[:, 0].reshape(150, 1)
X1 = X.iloc[:, 1].reshape(150, 1)
X2 = X.iloc[:, 2].reshape(150, 1)
X3 = X.iloc[:, 3].reshape(150, 1)
J = pd.Series(np.arange(800, dtype = float))
for i in range(800):
# theta j := theta j + alpha*(yi - h(xi))*xi
temp[0] = theta_g[0] + alpha*np.sum((Y- dot(X, theta_g))*X0)/150.
temp[1] = theta_g[1] + alpha*np.sum((Y- dot(X, theta_g))*X1)/150.
temp[2] = theta_g[2] + alpha*np.sum((Y- dot(X, theta_g))*X2)/150.
temp[3] = theta_g[3] + alpha*np.sum((Y- dot(X, theta_g))*X3)/150.
J[i] = 0.5*np.sum((Y - dot(X, theta_g))**2) #计算损失函数值
theta_g = temp #更新theta print theta_g
print J.plot(ylim = [0, 50])
代码所用的数据下载地址:http://files.cnblogs.com/files/sumai/iris.rar
5.局部加权回归(LWR)
当遇到类似下面情况的数据时,我们用简单的线性回归去拟合的话显然不合适,这时候局部加权回归就适用了。局部加权回归的思想是重点考虑你输入特征X附近的情况,同时不那么重视离你输入特征较远的情况,这就是所谓的“局部加权”。如下图所示,当我们要预测X大约为-1时,Y的值。这时候我就重点考虑X=-1附近的点,然后拟合出回归直线,作出预测。
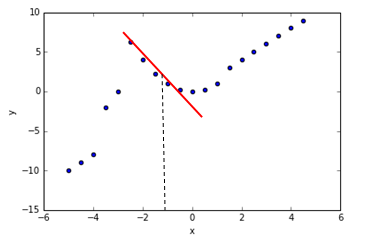
局部加权回归的损失函数为:
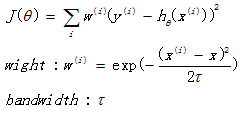
与线性回归的损失函数相比,多了一个w权值。其中 x 是要预测的特征,这样假设的道理是离 x 越近的样本权重越大,越远的影响越小。τ是带宽参数,用来调节“局部”的大小。
求出参数θ的方法有以下两种
批量梯度下降法:θj := θj − α· ∂J(θ)/∂θj (j = 0,1,...,n, α为学习速率, J(θ)/∂θj 为J的偏导数) 不断同时更新θj直到收敛
正规方程法: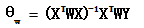
线性回归模型(Linear Regression)及Python实现的更多相关文章
- Python - 线性回归(Linear Regression) 的 Python 实现
背景 学习 Linear Regression in Python – Real Python,前面几篇文章分别讲了"regression怎么理解","线性回归怎么理解& ...
- 机器学习经典算法具体解释及Python实现--线性回归(Linear Regression)算法
(一)认识回归 回归是统计学中最有力的工具之中的一个. 机器学习监督学习算法分为分类算法和回归算法两种,事实上就是依据类别标签分布类型为离散型.连续性而定义的. 顾名思义.分类算法用于离散型分布预測, ...
- Python 线性回归(Linear Regression) - 到底什么是 regression?
背景 学习 Linear Regression in Python – Real Python,对 regression 一词比较疑惑. 这个 linear Regression 中的 Regress ...
- Python 线性回归(Linear Regression) 基本理解
背景 学习 Linear Regression in Python – Real Python,对线性回归理论上的理解做个回顾,文章是前天读完,今天凭着记忆和理解写一遍,再回温更正. 线性回归(Lin ...
- 从损失函数优化角度:讨论“线性回归(linear regression)”与”线性分类(linear classification)“的联系与区别
1. 主要观点 线性模型是线性回归和线性分类的基础 线性回归和线性分类模型的差异主要在于损失函数形式上,我们可以将其看做是线性模型在多维空间中“不同方向”和“不同位置”的两种表现形式 损失函数是一种优 ...
- 机器学习之多变量线性回归(Linear Regression with multiple variables)
1. Multiple features(多维特征) 在机器学习之单变量线性回归(Linear Regression with One Variable)我们提到过的线性回归中,我们只有一个单一特征量 ...
- 【深度学习】线性回归(Linear Regression)——原理、均方损失、小批量随机梯度下降
1. 线性回归 回归(regression)问题指一类为一个或多个自变量与因变量之间关系建模的方法,通常用来表示输入和输出之间的关系. 机器学习领域中多数问题都与预测相关,当我们想预测一个数值时,就会 ...
- 从零单排入门机器学习:线性回归(linear regression)实践篇
线性回归(linear regression)实践篇 之前一段时间在coursera看了Andrew ng的机器学习的课程,感觉还不错,算是入门了. 这次打算以该课程的作业为主线,对机器学习基本知识做 ...
- 多重线性回归 (multiple linear regression) | 变量选择 | 最佳模型 | 基本假设的诊断方法
P133,这是第二次作业,考察多重线性回归.这个youtube频道真是精品,用R做统计.这里是R代码的总结. 连续变量和类别型变量总要分开讨论: 多重线性回归可以写成矩阵形式的一元一次回归:相当于把多 ...
- 【342】Linear Regression by Python
Reference: 用scikit-learn和pandas学习线性回归 首先获取数据存储在 pandas.DataFrame 中,获取途径(CSV 文件.Numpy 创建) 将数据分成 X 和 y ...
随机推荐
- 从研究try catch 捕获不到异步错误谈谈学习方法的问题
先看下面的代码,思考一下输出 try { throw new Error(3) } catch (e) { console.log(e) } try { setTimeout(function () ...
- python request post
import requests import json class BaiduTranslateSpider: def __init__(self, kw): self.url = "htt ...
- mingw-w64线程模型:posix vs win32(posix允许使用c++11的std:: thread,但要带一个winpthreads,可能需要额外dll)
我正在安装 mingw-w64 on Windows,有两个选项: win32线程和posix线程. 我知道win32线程和pthreads之间的区别,但是我不明白这两个选项之间的区别. 我怀疑如果我 ...
- Bit error testing and training in double data rate (ddr) memory system
DDR PHY interface bit error testing and training is provided for Double Data Rate memory systems. An ...
- mongose TypeError: Cannot read property 'findOne' of undefined
最近在node的一个项目中,需要在model的一个数据表中写一个钩子函数去调用另外一个文件中的方法,一开始我采用了将此方法放入到global中,直接从global.meteod这样去获取.后来我又尝试 ...
- OVS 派OFPT_PORT_STATUS 流程
依据openflow合约[OFP1.0-38],当从物理端口ovs datapath 添加,改动或者删除的时候.都会先运行详细动作.然后通过ofp_port_status异步消息告知Controlle ...
- 发布与订阅SQLServer
SQLServer 中发布与订阅 在对数据库做迁移的时候,会有很多方法,用存储过程,job,也可以用开源工具lettle,那么今天这些天变接触到了一种新的方法,就是SqlServer中自带的发布与订阅 ...
- C#与西门子PLC通讯
1.0 通讯组件概述 通讯组件用于PC与可编程控制器(PLC).智能仪表等进行数据通讯,适用于基于PC高级语言的工业自动化控制系统.组件采用动态链接库文件(*.DLL)的形式,在PC系统的项目工程里 ...
- Matlab Tricks(十五) —— 圆的正确画法
使用参数方程, phi = 0:0.01:2*pi; x = cos(phi); y = sin(phi); axis equal plot(x, y) 根据参数方程,显然,圆心在 (0, 0),半径 ...
- python 两个链表的第一个公共结点
题目描述 输入两个链表,找出它们的第一个公共结点. 看到这道题的时候,很多人的第一反应就是采用蛮力的方法:在第一个链表上顺序遍历每个节点,每遍历到一个节点的时候,在第二个链表上顺序遍历每个节点.如 ...
