BP神经网络测试MNIST记录

约定：

所有的初始化权值范围，如下，就是说更换激活函数的情况，没有过大的调整初始权重。

         if(randomMode==1):
             numpy.random.seed(seedWih)
             self.wih = numpy.random.rand(self.hNodes, self.iNodes)-0.5
             numpy.random.seed(seedWho)
             self.who = numpy.random.rand(self.oNodes, self.hNodes)-0.5
         else:
             numpy.random.seed(seedWih)
             self.wih = numpy.random.normal (0.0, pow(self.hNodes,-0.5), (self.hNodes, self.iNodes))
             numpy.random.seed(seedWho)
             self.who = numpy.random.normal (0.0, pow(self.oNodes,-0.5), (self.oNodes, self.hNodes))
   

证明神经网络具有学习能力的方案：

为了减少测试时间，

将MNIST_100迭代训练较多次。

然后将其作为测试数据。如果出现了过拟合状态，承认通过训练其具有学习能力。可以进行下述测试：

参数含义：

输入层节点/隐层结点/输出层节点/学习率/初始化权重的分布方案/输入层和隐层的初始化种子/输出层和隐层的初始化种子/使用的激活函数

激活函数为：softmax:

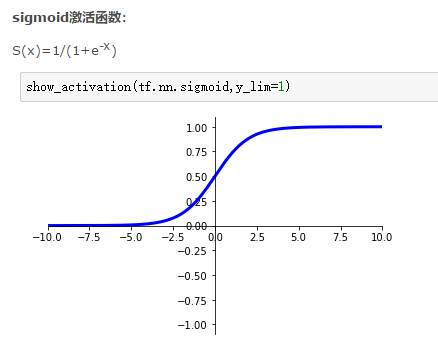
训练1代，达到95.17%的测试识别率。参数为：784/100/10/0.1、rand、4、5、softmax.

训练2代，达到96.16%的测试识别率。参数为：784/100/10/0.1、rand、4、5、softmax.

训练3代，达到96.52%的测试识别率。参数为：784/100/10/0.1、rand、4、5、softmax.

训练4代，达到96.43%的测试识别率。参数为：784/100/10/0.1、rand、4、5、softmax.

训练5代，达到96.56%的测试识别率。参数为：784/100/10/0.1、rand、4、5、softmax.

训练6代，达到96.41%的测试识别率。参数为：784/100/10/0.1、rand、4、5、softmax.

调试参数如下：

inputs = numpy.asfarray( all_values [1:])/255.0*0.99+0.01
targets = numpy.zeros(self.nN.oNodes) + 0.01
targets[int (all_values[0])] = 0.99

fx1=numpy.exp(-final_inputs)/((1+numpy.exp(-final_inputs))*(1+numpy.exp(-final_inputs)))
fx2=numpy.exp(-hidden_inputs)/((1+numpy.exp(-hidden_inputs))*(1+numpy.exp(-hidden_inputs)))

self.who += self.lr * numpy.dot((output_errors * fx1),numpy.transpose(hidden_outputs))
self.wih += self.lr * numpy.dot((hidden_errors * fx2),numpy.transpose(inputs))

激活函数为：softsign:

一点说明：

为什么学习率取值这样

sigmoid*2-1

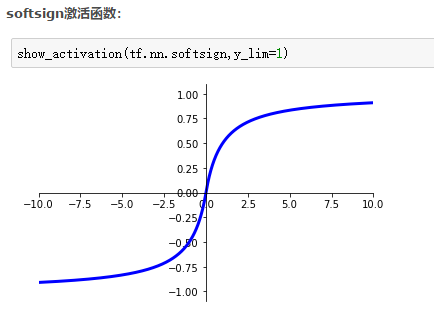
训练5代，达到65.58%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

训练10代，达到74.39%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

训练15代，达到76.49%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

训练20代，达到83.34%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

训练25代，达到91.8%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

训练30代，达到92.43%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

训练35代，达到92.54%的测试识别率。参数为：784/80/10/0.05、normal、4、5、softsign.

调试参数如下：

inputs = numpy.asfarray( all_values [1:])/255.0*0.5
targets = numpy.zeros(self.nN.oNodes) -0.99
targets[int (all_values[0])] = 0.99

fx1=numpy.exp(-final_inputs)/((1+numpy.exp(-final_inputs))*(1+numpy.exp(-final_inputs)))
fx2=numpy.exp(-hidden_inputs)/((1+numpy.exp(-hidden_inputs))*(1+numpy.exp(-hidden_inputs)))

self.who += self.lr * numpy.dot((output_errors * fx1),numpy.transpose(hidden_outputs))
self.wih += self.lr * numpy.dot((hidden_errors * fx2),numpy.transpose(inputs))

激活函数为：tanh:

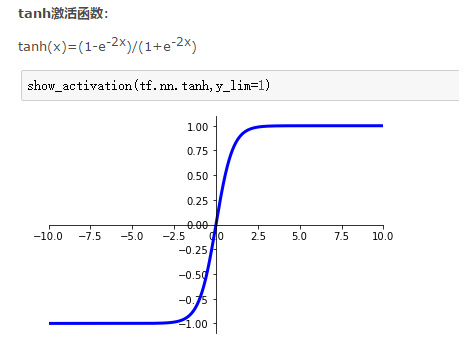
训练1代，达到93.57%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

训练2代，达到94.44%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

训练3代，达到94.73%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

训练4代，达到94.47%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

训练5代，达到95.05%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

训练6代，达到95.33%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

训练7代，达到94.86%的测试识别率。参数为：784/80/10/0.05、normal、4、5、tanh.

调试参数如下：

inputs = numpy.asfarray( all_values [1:])/255.0*0.5
targets = numpy.zeros(self.nN.oNodes) -0.99
targets[int (all_values[0])] = 0.99

fx1=numpy.exp(-2*final_inputs)/((1+numpy.exp(-2*final_inputs))*(1+numpy.exp(-2*final_inputs)))
fx2=numpy.exp(-2*hidden_inputs)/((1+numpy.exp(-2*hidden_inputs))*(1+numpy.exp(-2*hidden_inputs)))

self.who += self.lr * numpy.dot((output_errors * fx1),numpy.transpose(hidden_outputs))
self.wih += self.lr * numpy.dot((hidden_errors * fx2),numpy.transpose(inputs))

激活函数为：relu:

部分说明：

关于学习率。过大的学习率导致学习能力丢失，如0.1的学习率在这里过大。

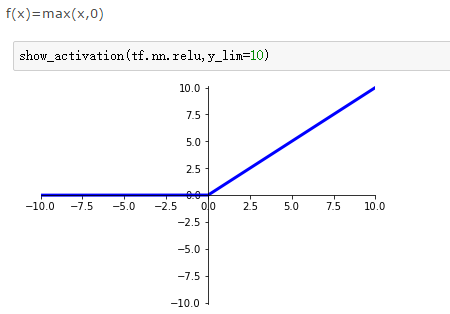
训练1代，达到95.34%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练2代，达到96.12%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练3代，达到96.65%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练4代，达到96.8%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练5代，达到96.95%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练6代，达到97.08%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练7代，达到97.32%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

训练8代，达到97.23%的测试识别率。参数为：784/100/10/0.001、rand、4、5、relu.

调试参数如下：

inputs = numpy.asfarray( all_values [1:])/255.0*0.99+0.01
targets = numpy.zeros(self.nN.oNodes) + 0.01
targets[int (all_values[0])] = 10

final_inputs[final_inputs>0]=1
hidden_inputs[hidden_inputs>0]=1
final_inputs[final_inputs<0]=0
hidden_inputs[hidden_inputs<0]=0
fx1=final_inputs;fx2=hidden_inputs

self.who += self.lr * numpy.dot((output_errors * fx1),numpy.transpose(hidden_outputs))
self.wih += self.lr * numpy.dot((hidden_errors * fx2),numpy.transpose(inputs))

激活函数为：softplus:

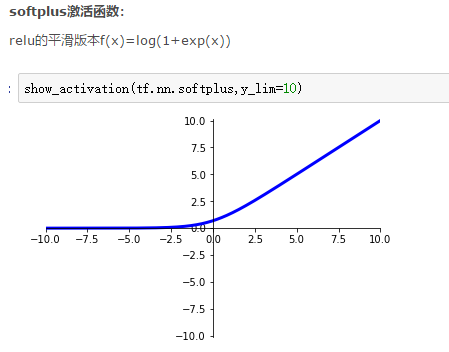
训练1代，达到95.62%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练2代，达到96.47%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练3代，达到96.85%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练4代，达到97.06%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练5代，达到97.18%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练6代，达到97.29%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练7代，达到97.34%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练8代，达到97.39%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练9代，达到97.5%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练10代，达到97.54%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练11代，达到97.61%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

训练12代，达到97.6%的测试识别率。参数为：784/100/10/0.001、rand、4、5、softplus.

调试参数如下：

inputs = numpy.asfarray( all_values [1:])/255.0*0.99+0.01
targets = numpy.zeros(self.nN.oNodes) + 0.01
targets[int (all_values[0])] = 10

fx1=numpy.exp(final_inputs)/(1+numpy.exp(final_inputs))
fx2=numpy.exp(hidden_inputs)/(1+numpy.exp(hidden_inputs))

self.who += self.lr * numpy.dot((output_errors * fx1),numpy.transpose(hidden_outputs))
self.wih += self.lr * numpy.dot((hidden_errors * fx2),numpy.transpose(inputs))