思考的乐趣----matrix67数学笔记:最精妙的无字证明
从《思考的乐趣----matrix67数学笔记》一书中看到这个证明,据说在mathoverflow网站上这个无字证明获得了最多的投票!
http://mathoverflow.net/questions/8846/proofs-without-words
认真思考了该图的含义,终于恍然大悟,果然是精妙绝伦的无字证明!
==================
下
面
是
我
的
理
解
==================
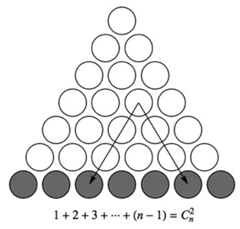
最底层的一排圆表示第n层,排列组合里的C(n,2)=n*(n-1)/2,表示从n个圆里任意选2个,从底下任意2个圆向上的连线相交的小圆就是对应于一种组合,随便地在底层选2个圆,都会对应于上面的一个空心圆!
个人感兴趣的是以下几章:
读书笔记:《思考的乐趣》第12章 让你立刻爱上数学的8个算术游戏
思考的乐趣----matrix67数学笔记:最精妙的无字证明的更多相关文章
- 读书笔记:《思考的乐趣:Matrix67数学笔记》第4章 统计数据的陷阱
<思考的乐趣:Matrix67数学笔记>第4章讲了几个统计学上的陷阱,由于现在流行的大数据与统计学很有渊源,所以认真读了这一章,在<大数据时代>中指出只考虑相关性就够了,而不考 ...
- [数学笔记Mathematical Notes]目录
2.也许是一个问题,暂时没给出解答. 2015年7月5日 1. 这个一个笔记类型的数学杂志, 打算用来记录自己学数学时做的笔记,一般几页纸一期. 觉得有意思就摘抄下来,或者自己的感想. 可能有些不是原 ...
- 【读书笔记与思考】Andrew 机器学习课程笔记
Andrew 机器学习课程笔记 完成 Andrew 的课程结束至今已有一段时间,课程介绍深入浅出,很好的解释了模型的基本原理以及应用.在我看来这是个很好的入门视频,他老人家现在又出了一门 deep l ...
- AI与数学笔记之深入浅出的讲解傅里叶变换(真正的通俗易懂)
原文出处: 韩昊 # 作 者:韩 昊 # 知 乎:Heinrich # 微 博:@花生油工人 # 知乎专栏:与时间无关的故事 # 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张 ...
- [数学笔记Mathematical Notes]2-一个带对数的积分不等式
定理. $$\bex \int_0^1\frac{\ln^2x}{x^x}\rd x<2\int_0^1 \frac{\rd x}{x^x}. \eex$$ 证明: 由分部积分及 Fubini ...
- [数学笔记Mathematical Notes]1-调和级数发散的一个简单证明
定理. 调和级数 $\dps{\vsm{n}\frac{1}{n}}$ 是发散的. 证明. 设 $$\bex a_n=\sum_{k=1}^n\frac{1}{k}, \eex$$ 则 $a_n$ 递 ...
- [数分笔记]用Dedekind切割定理证明确界定理
1.定理内容 Dedekind切割定理:设是实数集的一个切割,则或者有最大数,或者有最小数. 确界定理:非空有上界的数集必有上确界,非空有下界的数集必有下确界. 2.证明过程 设非空数集有上界 记,即 ...
- [数分笔记]Dedekind切割定理的证明
1.定理内容 Dedekind切割定理:设是实数集的一个切割,则或者有最大数,或者有最小数. 2.证明过程 设是中所有有理数所构成的集合,是中所有有理数所构成的集合 从而构成一个有理数集的切割 有三种 ...
- GTD3年来读的52本书
2012年 1.一生的计划 平衡:人生要在精神.理财.教育和娱乐4个方面进行平衡. 2.重来REWORK 小型软件公司的创业与软件项目的管理 不要管全年计划,只要找出下一项最重要的任务,然后起 ...
随机推荐
- photoshop cs6安装过程中安装程序遇到错误:请重启计算机,解决办法
1.关闭防火墙和杀毒软件 2.删除注册表 依次展开HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\Session Manager目录,找到其中的 ...
- Leetcode(力扣) 整数反转
Leetcode 7.整数反转 给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转. 示例: 输入: -123 输出: -321 注意: 假设我们的环境只能存储得下 32 位的有符 ...
- Nuxeo 认证绕过和RCE漏洞分析(CVE-2018-16341)
简介 Nuxeo Platform是一款跨平台开源的企业级内容管理系统(CMS).nuxeo-jsf-ui组件处理facelet模板不当,当访问的facelet模板不存在时,相关的文件名会输出到错误页 ...
- Day Ten
站立式会议 站立式会议内容总结 331 今天:话题单选对话框 遇到问题:无 442 今天:数据库交互,解决timepicker问题 遇到的问题:无 439 今天:测试模块功能 遇到问题:无 会议照片 ...
- 基于RYU的拓扑发现
基于RYU的拓扑发现 前言 本次实验是一个基于RYU的拓扑发现功能.参考了呈神的实现方式,并加了一些自己实现方式,做了一些数据结构的改动. 数据结构 link_to_port 字典 有两种关系: 一是 ...
- (第三周)c#程序理解
阅读下面程序,请回答如下问题: 问题1:这个程序要找的是符合什么条件的数? 问题2:这样的数存在么?符合这一条件的最小的数是什么? 问题3:在电脑上运行这一程序,你估计多长时间才能输出第一个结果?时间 ...
- C#程序分析
一.程序及问题 阅读下面程序,请回答如下问题: 问题1:这个程序要找的是符合什么条件的数? 问题2:这样的数存在么?符合这一条件的最小的数是什么? 问题3:在电脑上运行这一程序,你估计多长时间才能输出 ...
- pandas读取csv数据时设置index
比如读取数据时想把第一列设为index,那么只需要简单的 pd.read_csv("new_wordvecter.csv",index_col=[0]) 这里index_col可以 ...
- _stdcall 和 _cdecl
今天遇到一个问题用C++编写一个动态链接库生成的文件为dll.dll,用在visual stdio 2010调用这个dll 调用形式:[DllImport("dll.dll")] ...
- Linux命令学习chroot和chmode
chroot:chang root http://man.linuxde.net/chroot https://baike.baidu.com/item/chroot 1.限制被CHROOT的使用者所 ...
