用蒙特卡罗方法解非线性规划MATLAB

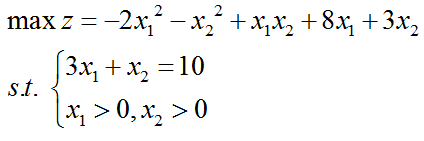
共需要三个M文件，主程序为randlp.m

randlp.m:

function [sol,r1,r2]=randlp(a,b,n)          %随机模拟解非线性规划
debug=1;
a=0;                                          %试验点下界
b=10;                                         %试验点上界
n=1000;                                      %试验点个数
r1=unifrnd(a,b,n,1);                    %nx1阶的[a,b]均匀分布随机数矩阵
r2=unifrnd(a,b,n,1);
sol=[r1(1) r2(1)];
z0=inf;

for i=1:n
   x1=r1(i);
   x2=r2(i);
   lpc=lpconst([x1 x2]);
   if lpc==1
      z=mylp([x1 x2]);
      if z<z0
         z0=z;
         sol=[x1 x2];
      end
   end
end
z=z0

　　mypl.m:

function z=mylp(x)
z=2*x(1)^2+x(2)^2-x(1)*x(2)-8*x(1)-3*x(2);

　　lpconst.m:

function lpc=lpconst(x)
if 3*x(1)+x(2)-10<=0.5 & 3*x(1)+x(2)-10>=-0.5
   lpc=1;
else
   lpc=0;
end

　结果：x₁=2.524,x₂=2.8397,z=15.0735