luoguP1029 最大公约数和最小公倍数问题 [gcd][数论]

题目描述

输入二个正整数x0,y0(2<=x0<100000,2<=y0<=1000000),求出满足下列条件的P,Q的个数

条件:

1.P,Q是正整数

2.要求P,Q以x0为最大公约数,以y0为最小公倍数.

试求:满足条件的所有可能的两个正整数的个数.

输入输出格式

输入格式：

二个正整数x0,y0

输出格式：

一个数，表示求出满足条件的P,Q的个数

输入输出样例

输入样例#1：

3 60

输出样例#1：

4

说明

P,Q有4种

3 60 15 12 12 15 60 3

---

先考虑对P,Q进行质因数分解，得到

然后，

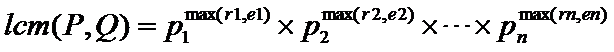
gcd同理，把max改成min就好了。

那么，对于把gcd为x，lcm为y的P,Q，若ri,ei不同，则有两种情况；

　　　　　　　　　　　　　　　　　若ri与ei相等，则只有一种情况。

对P,Q分解质因数，统计质因数pi项二者的指数不同的项数ens，答案就是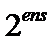

ps:

1.可以做一些预先的判断，比如若x不整除于y，则答案必然为0。

2.可以令k=y/x，对k做质因数分解即可。

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 #include<cmath>
 using namespace std;

 int x,y,k,ens=;

 int main(){
     scanf("%d%d",&x,&y);
     if(y%x){
         puts("");
         return ;
     }
     k=y/x;
     for(int i=;k!=;i++){
         if(k%i==){
             ens++;
             while(k%i==)  k/=i;
         }
     }
     printf("%.0lf\n",pow(,ens));
     return ;
 }