Huffman树及其编码(STL array实现)

这篇随笔主要是Huffman编码，构建哈夫曼树有各种各样的实现方法，如优先队列，数组构成的树等，但本质都是堆。

这里我用数组来存储数据，以堆的思想来构建一个哈弗曼树，并存入vector中，进而实现哈夫曼编码

　

步骤：　　1生成哈夫曼树  （取最小权值树和次小权值树生成新树，排列后重新取树，不断重复）

　　　　    2编码   （遵循左零右一的原则）

　　           3解码（是编码的逆向，本文还未实现，日后有机会补充）

data.txt  测试数据：

5
1 2 3 4 5
abcde

结果：

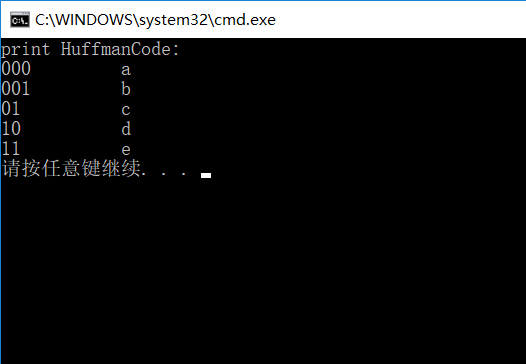
下面贴代码：

 #include <iostream>
 #include <fstream>
 #include <algorithm>
 #include <vector>
 #include <array>

 using namespace std;

 #define ARR_SIZE 100   //缓冲区大小

 typedef struct Tree
 {
     int freq;
     char key = '\0';
     Tree *left, *right;
     Tree()
     {
         freq = ;
         key = '\0';
         left = NULL;
         right = NULL;
     }
 } Tree, *pTree;
 union key_or_point
 {
     char key;
     pTree point;
 };
 enum infor_type
 {
     key_s,
     point_s
 };
 class infor
 {
 public:
     int freq;//权值
     key_or_point kp;//记录键值或者 新生成的树的地址
     infor_type type;//  联合体key_or_point的类型由infor_type标志
     infor()
     {
         freq = ;
         kp.key = NULL;
         type = key_s;
     }
 };

 array<infor, ARR_SIZE> arr;//用来读取要处理的数据
 vector<pTree> trees;  //所有生成的树都放在vector里面

 int num;   //要处理的数据个数

 bool cmp(infor a, infor b)
 {
     return a.freq > b.freq;
 }

 void Huffman()
 {
     //找出最小权值和次小权值
     sort(&arr[], &arr[num], cmp);
     int cal = num - ;
     while (cal > )
     {

         pTree pta = new Tree();
         vector<pTree>::iterator it;

         pTree ptl = new Tree();
         ptl->freq = arr[cal].freq;
         // pt all 的左子树
         if (arr[cal].type == point_s)
         {
             pta->left = arr[cal].kp.point;//如果存放的是地址，那么该树已入vector
             //无需重复操作
         }
         else
         {
             ptl->key = arr[cal].kp.key;
             trees.push_back(ptl);
             it = trees.end() - ;
             pta->left = *it;
         }

         pTree ptr = new Tree();
         ptr->freq = arr[cal - ].freq;
         // pt all 的右子树
         if (arr[cal - ].type == point_s)
         {
             pta->right = arr[cal - ].kp.point; //如果存放的是地址，那么该树已入vector
             //无需重复操作
         }
         else
         {
             ptr->key = arr[cal - ].kp.key;
             trees.push_back(ptr);
             it = trees.end() - ;
             pta->right = *it;
         }

         pta->freq = arr[cal].freq + arr[cal - ].freq;
         trees.push_back(pta);//pt all 本树

         it = trees.end() - ;
         arr[cal - ].kp.point = *it;
         arr[cal - ].type = point_s;//保存新生成树的地址

         arr[cal - ].freq = arr[cal - ].freq + arr[cal ].freq;
         //最小权值的树和次权值的树组成新树后，放回原数组
         //新树的key_or_point此时类型变为point_s指针指向vector存放的位置

         //第一次循环会有三棵树入vector,重新排列后，新树无需重复入vector
         cal--;
         sort(&arr[], &arr[cal + ], cmp);

     }

 }

 void traversTree(pTree pt, string st = "")
 {
     //中序遍历二叉树
     //遵循左0右1的原则
     if (pt->left == NULL && pt->right == NULL)
     {
         cout.flags(ios::left);
         cout.width();
         cout << st.c_str() << "  ";
         cout << pt->key << endl;
         return;
     }
     if (pt->left != NULL)
     {
         st += '';
         traversTree(pt->left, st);
         st.pop_back();//从左边出来后要回退一个字符，避免进入右边时多出一个字符
     }

     if (pt->right != NULL)
     {
         st += '';
         traversTree(pt->right, st);
     }
     return ;
 }

 void printCode()
 {
     vector<pTree>::iterator it;
     it = trees.end() - ;
     pTree pt = *it; //取出最顶端的树
     cout << "print HuffmanCode:" << endl;
     traversTree(pt);
 }
 int main()
 {
     ifstream filein("data.txt");
     cin.rdbuf(filein.rdbuf());//重定向输入
     cin >> num;//要处理的数据个数
     for (int i = ; i < num; i++)
     {
         cin >> arr[i].freq;
     }
     for (int i = ; i < num; i++)
     {
         cin >> arr[i].kp.key;
     }
     Huffman();
     printCode();
     return ;
 }

分析：

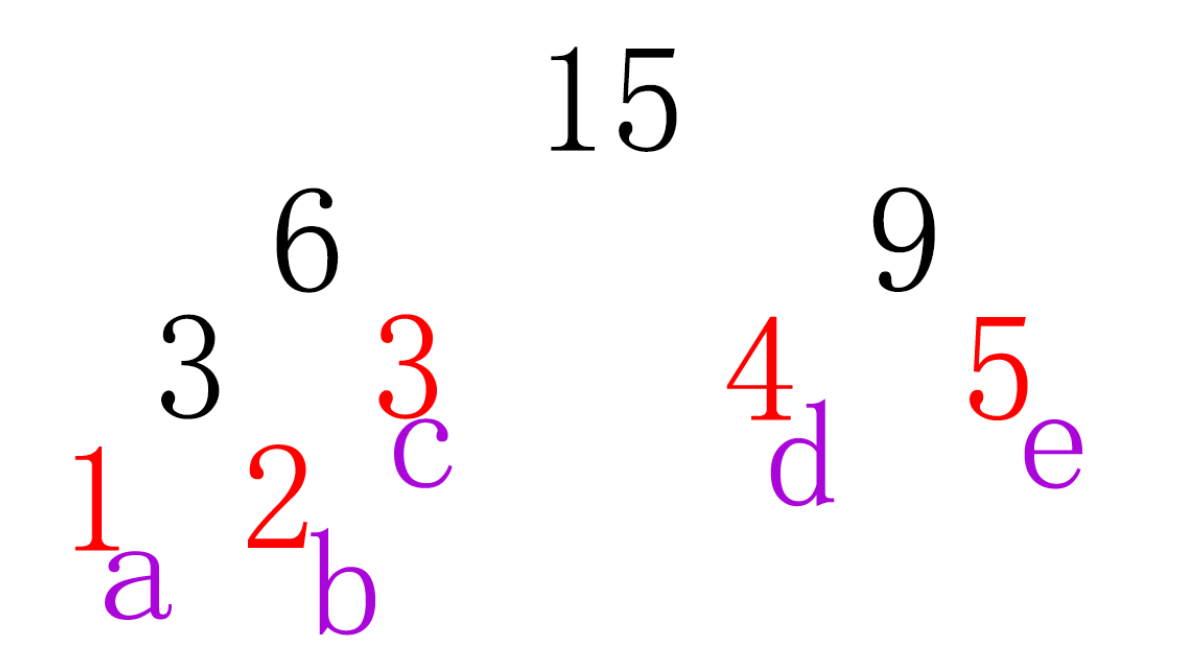
这是以上测试数据生成的树的情况。

只有叶子节点表示有效的符号，所以遍历树时返回条件是叶子节点（如果是叶子节点则返回）

总结：

1 编程时用的一些小技巧总结：

　　1.1  输出调试信息：可以采用如下方式

　　　　　　#ifdef DEBUG

　　　　　　　　cout调试信息....

　　　　　　#endif

　　1.2 联合体union需要取得类型时，可以加一个enum来记录和标志uninon的类型

2  编程方法反思：

　　可以看到源码中用到了两次sort，这是省事的做法了。

　　目前想到的改进的方法是用二分插入（数据已经排序）

　　

　　对比起来，我觉得优先队列的方式更易懂且效率更高，但此文也算是一次小探索，值得记录下来

3 感想：

　　本人入园第一次随笔，如有不足或错误，还望指出。

以上