BZOJ 1010: [HNOI2008]玩具装箱toy（斜率优化dp）

http://www.lydsy.com/JudgeOnline/problem.php?id=1010

题意：

思路：

容易得到朴素的递归方程：$dp(i)=min(dp(i),dp(k)+(i-k-1+sum[i]-sum[k]-l)^{2})$，$sum[i]$表示前i个玩具的$c_{i}$之和。$f(k)$表示前k个玩具的最小费用。

如果设$f(i)=sum[i]+i$，那么上式就可以改写为$dp(i)=min(dp(i),dp(k)+(f(i)-f(k)-l-1)^{2})$。

所以这道题目是很明显的斜率优化dp。

如果k决策比j决策更优的话，那么（c=l+1）

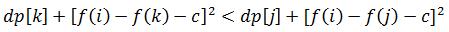
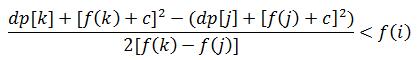
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<sstream>
 #include<vector>
 #include<stack>
 #include<queue>
 #include<cmath>
 #include<map>
 #include<set>
 using namespace std;
 typedef long long ll;
 typedef pair<int,ll> pll;
 const int INF = 0x3f3f3f3f;
 const int maxn=+;

 ll n, l;
 ll c[maxn];
 ll dp[maxn];
 ll sum[maxn];
 ll Q[maxn];

 ll dy(ll k, ll j)
 {
     return dp[k]+(sum[k]+l)*(sum[k]+l)-dp[j]-(sum[j]+l)*(sum[j]+l);
 }

 ll dx(ll k, ll j)
 {
     return *(sum[k]-sum[j]);
 }

 int main()
 {
     //freopen("in.txt","r",stdin);
     while(~scanf("%lld%lld",&n,&l))
     {
         l+=;
         sum[]=;
         for(int i=;i<=n;i++)
         {
             scanf("%I64d",&c[i]);
             sum[i]=sum[i-]+c[i];
         }
         for(int i=;i<=n;i++)  sum[i]+=i;
         Q[]=;
         int frt=,rear=;
         for(int i=;i<=n;i++)
         {
             while(frt<rear && dy(Q[frt+],Q[frt])<=sum[i]*dx(Q[frt+],Q[frt]))   frt++;
             int tmp=Q[frt];
             dp[i]=dp[tmp]+(sum[i]-sum[tmp]-l)*(sum[i]-sum[tmp]-l);
             while(frt<rear && dy(Q[rear],Q[rear-])*dx(i,Q[rear])>=dy(i,Q[rear])*dx(Q[rear],Q[rear-]))  rear--;
             Q[++rear]=i;
         }
         printf("%lld\n",dp[n]);
     }
     return ;
 }