Luogu P9646 SNCPC2019 Paper-cutting 题解 [ 紫 ] [ manacher ] [ 贪心 ] [ 哈希 ] [ BFS ]

Paper-cutting：思维很好，但代码很构式的 manacher 题。

蒟蒻 2025 年切的第一道题，是个紫，并且基本独立想出的，特此纪念。

判断能否折叠

我们先考虑一部分能折叠需要满足什么条件。显然，这一部分需要是一个长度为偶数的回文串。

那么横向和纵向会不会影响呢？答案是不会，因为横向折了之后，折过去的部分一定是对称的，那么只要原来某两列相等，这之后这两列还是相等的。我们可以画图理解：

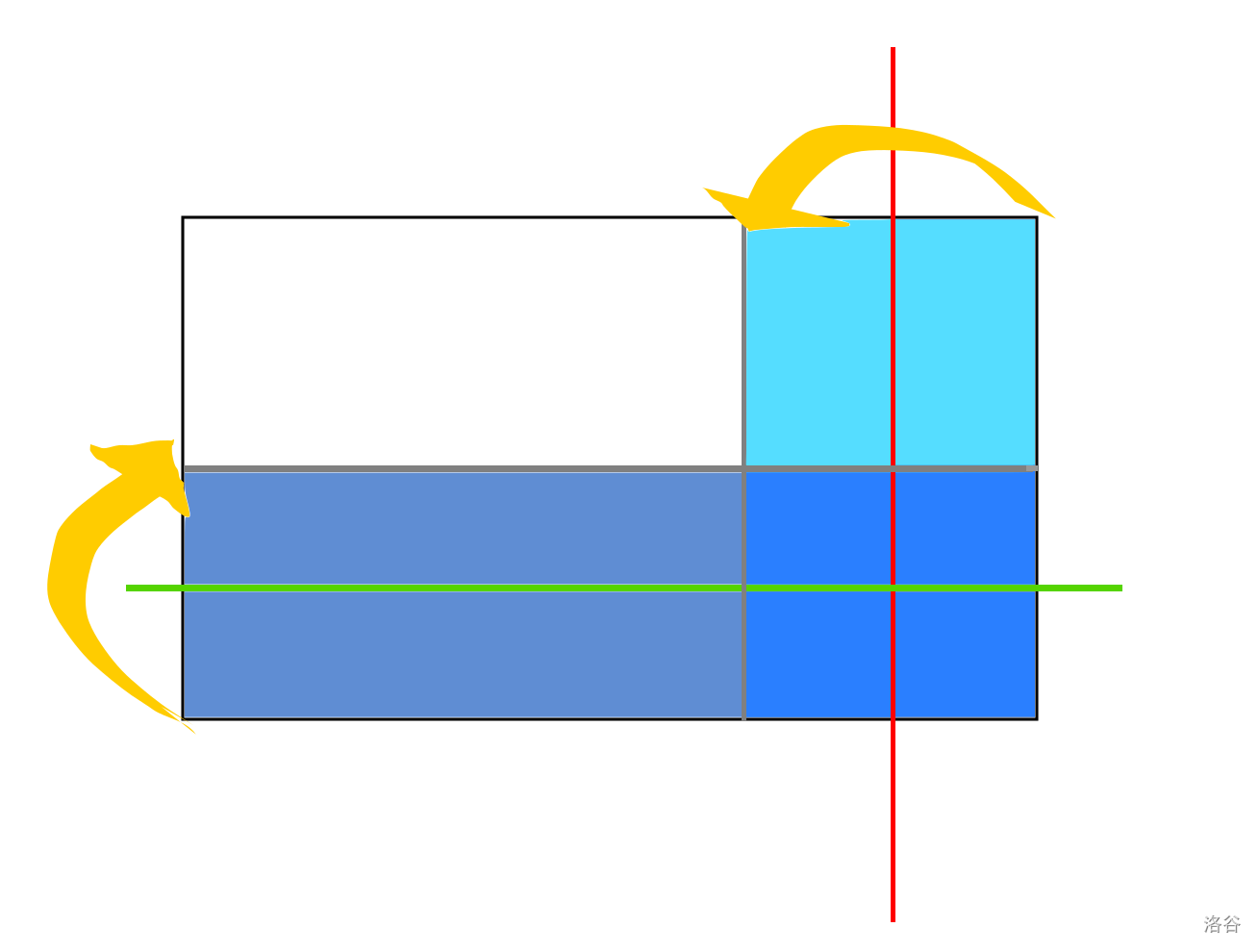
相同颜色的部分代表这两部分相等。

于是，我们只需要对每行每列哈希一遍，然后利用偶数回文串折叠即可。同时我们也得出横行和纵列互不影响的结论。

这一部分可以用 manacher 快速求出最大折叠半径。

折叠策略

我们先考虑这个问题的弱化版。

只能折一边时

在只能折一边时，我们一定会尽可能地折叠。这样一定更优。

证明也是容易的，折叠前折叠部分单独的连通块会被砍掉，与剩余部分相连接的连通块因为是对称过去，所以折叠过去后一定存在一个格子使它们依然连通。

因此，折叠后连通块的个数一定不会增加，答案也一定不劣。同时，折叠的顺序也是无影响的，因为每次能折叠当且仅当偶数回文串内存在一个能折叠到的点。

两边都能折时

同样是能折就折，因为左折、右折互不影响，我们可以用分类讨论来证明。

右折后左折能正常进行时

显然左右都能操作。

右折后左折被挡住一部分时

这种情况一定不存在。

左折要被挡住，必然要满足下图：

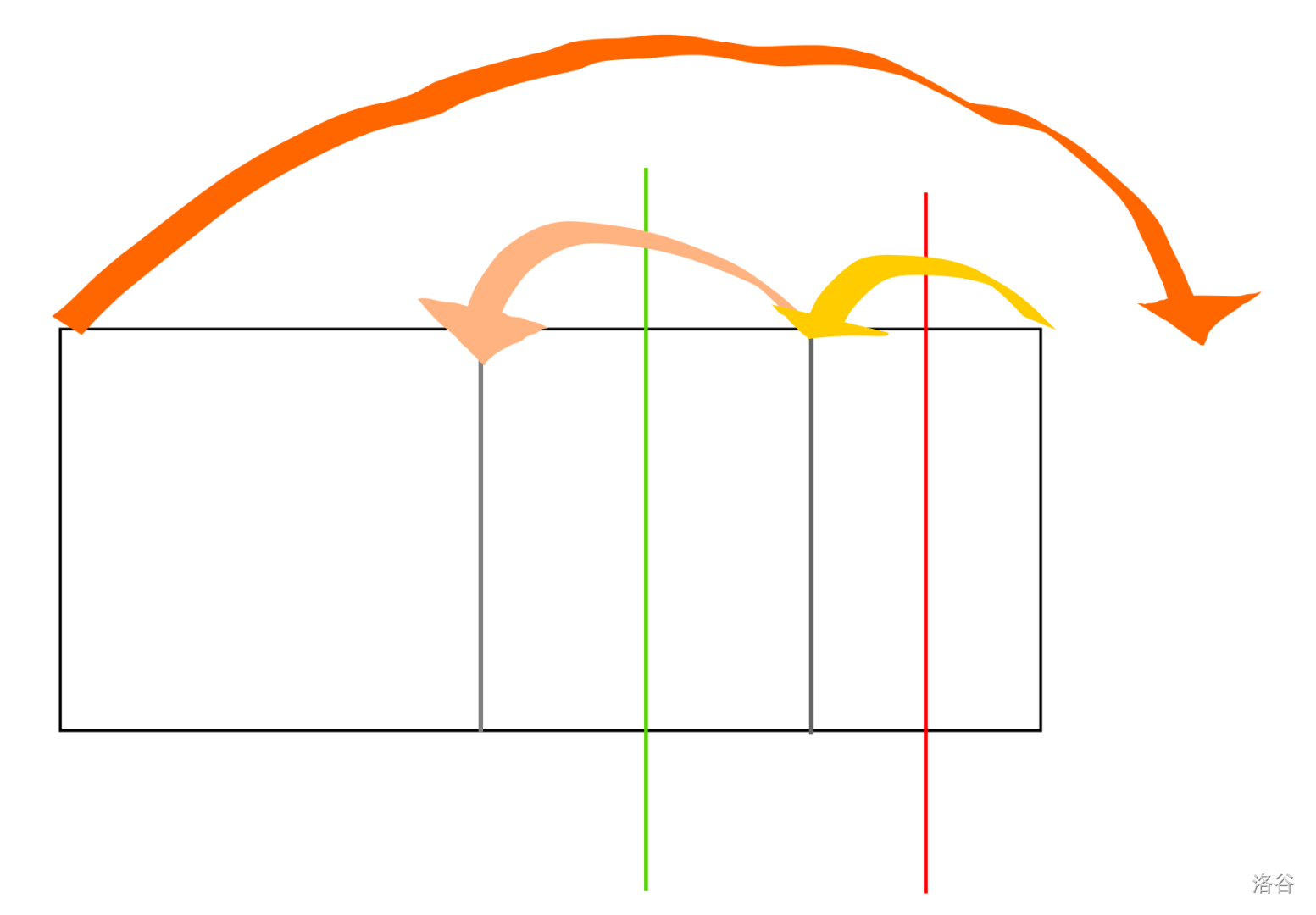
而橙色的左折显然不合法，这种情况等效于浅橙色部分右折。

因此能折就折的策略一定不劣。

翻折实现

对每行每列跑 manacher 记录最长回文长度后，我们考虑设计 dp。

以向左翻折为例，定义 \(dp_i\) 表示以 \(i\) 为最后一列是否可行，\(d_i\) 为回文半径长度，则：

\[dp_i=[(\sum_{j=i+1}^{i+d_i}dp_j) >0]
\]

这个式子可以用前缀和优化、单调队列优化来做，或者跟我一样维护一个最近的 \(1\) 的指针也可以。我本来用前缀和优化做的，但是挂了几十发并且还调不出就用其他题解一样的方式维护指针了。

注意初始化 \(dp_n=1\)。

向左翻折后，从左边开始再往右翻折一遍就可以了。注意不能翻过新的右边界。

最后求出左右边界、上下边界后，进行 BFS 求出需要减掉的连通块个数即可。

时间复杂度 \(O(nm)\)，注意动态开数组。

代码

非常构式，调了 2h。

#include <bits/stdc++.h>
#define fi first
#define se second
#define lc (p<<1)
#define rc ((p<<1)|1)
#define eb(x) emplace_back(x)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
using pi=pair<int,int>;
const ull nosol1=1145141919810,nosol2=1919810114514,nosol3=1911451419810;
int n,m,x,ansxl,ansxr,ansyl,ansyr,d[2000005];
int gox[]={0,0,1,-1};
int goy[]={-1,1,0,0};
vector<int>c[1000005];
ull xhs[1000005],yhs[1000005],f[2000005];
void init(int len,ull *arr)
{
    x=0;
    f[0]=nosol1;
    f[++x]=nosol2;
    for(int i=1;i<=len;i++)f[++x]=arr[i],f[++x]=nosol2;
    f[x+1]=nosol3;
}
void manacher()
{
    for(int i=1;i<=x;i++)d[i]=0;
    d[1]=1;
    for(int i=2,l=0,r=0;i<=x;i++)
    {
        if(i<=r)d[i]=min(r-i+1,d[l+r-i]);
        while(f[i-d[i]]==f[i+d[i]])d[i]++;
        if(i+d[i]-1>r)l=i-d[i]+1,r=i+d[i]-1;
    }
}
void do_dp(int len,int &ansl,int &ansr)
{
    ansr=len;
    for(int i=len-1;i>=1;i--)
    {
        int p=i*2+1;
        int dx=d[p]/2;
        if(i+dx>=ansr)ansr=i;
    }
    ansl=1;
    for(int i=1;i<ansr;i++)
    {
        int p=i*2+1;
        int dx=d[p]/2;
        if(i-dx+1<=ansl)ansl=i+1;
    }
}
bool legal(int x,int y){return (x>=ansxl&&x<=ansxr&&y>=ansyl&&y<=ansyr);}
void bfs(int x,int y)
{
    queue<pi>q;
    q.push({x,y});
    c[x][y]=1;
    while(!q.empty())
    {
        pi u=q.front();
        q.pop();
        int nx=u.fi,ny=u.se;
        for(int i=0;i<4;i++)
        {
            int tx=nx+gox[i],ty=ny+goy[i];
            if(legal(tx,ty)&&c[tx][ty]==0)
            {
                q.push({tx,ty});
                c[tx][ty]=1;
            }
        }
    }
}
void solve()
{
    int ans=0;
    cin>>n>>m;
    for(int i=1;i<=n;i++)c[i].clear();
    for(int i=1;i<=n;i++)xhs[i]=0;
    for(int i=1;i<=m;i++)yhs[i]=0;
    for(int i=1;i<=n;i++)
    {
        c[i].eb(0);
        for(int j=1;j<=m;j++)
        {
            char tmp;
            cin>>tmp;
            int k=tmp-'0';
            xhs[i]=xhs[i]*2+k;
            yhs[j]=yhs[j]*2+k;
            c[i].eb(k);
        }
    }
    init(n,xhs);
    manacher();
    do_dp(n,ansxl,ansxr);
    init(m,yhs);
    manacher();
    do_dp(m,ansyl,ansyr);
    for(int i=ansxl;i<=ansxr;i++)
    {
        for(int j=ansyl;j<=ansyr;j++)
        {
            if(c[i][j]==0)
            {
                ans++;
                bfs(i,j);
            }
        }
    }
    cout<<ans<<'\n';
}
int main()
{
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    int t;
    cin>>t;
    while(t--)solve();
    return 0;
}