【小 w 的代数】（提供一种 n^2 log 的解法）

前言：

卖点

记录 CTH 的发言

CTH：你这真是 n^3 的

CTH：我也不知道你线段树优化个啥，\(n^3 \log n\)

CTH：你优化到哪了啊

CTH：······你从赛时打这个题到现在 11 个小时了，你从 \(n^3\) 打到 \(n^3\log n\) 了

CTH：······再怎么着，我也不会一道题调三天

CTH：我一直都说这么打这么打，你打的是啥呀

CTH：你连题面都没弄懂呗

@CTHoi 黑子！叫！！！

不过还是要感谢 CTH 对这道题实现的大力支持与帮助，不然可能现在还调不出来呢

解法：

一句话以代之：微改线段树合并优化圆方树上 DP。

考虑 \(O(n^3)\) 的“暴力”做法：

对于每一个节点为根跑一遍 dfs，求出以该点为终点的路径有多少方案数，每次 dfs 进行以下树上 dp。

我们在回溯的时候用子节点更新父亲，那么就相当于我们求从叶子到根的递减路径，这样才可以优化。

设 \(f_{i,j}\) 表示以 \(i\) 号节点为根的子树中以 \(j\) 为终点的答案，有转移如下：

\[f_{u,i}=\sum_{u->v} \sum_{j=i+1}^n f_{v,j}
\]

这样树的部分就做完了，但有环的地方怎么办？如下图：

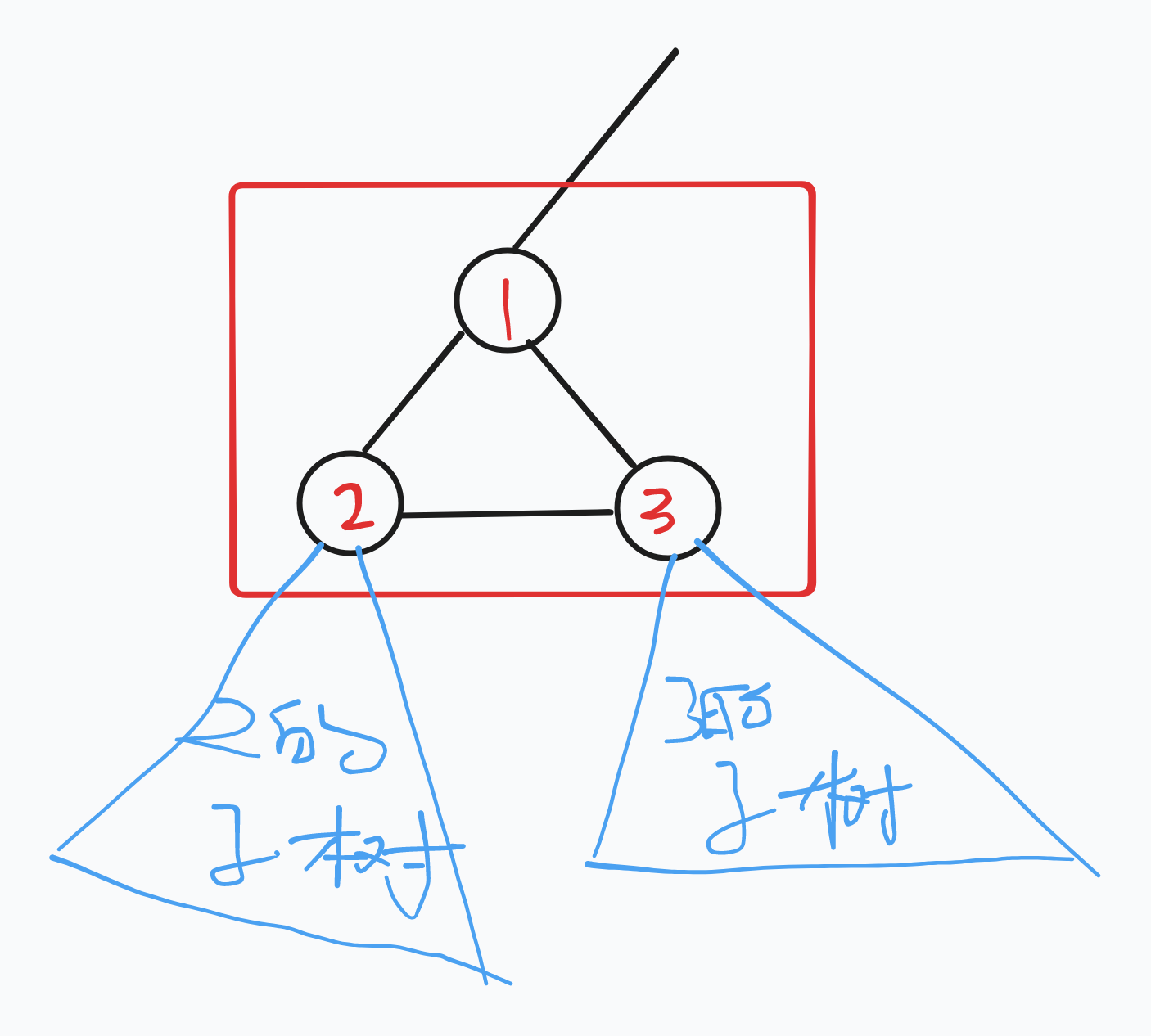
1 号点是 dfs 过程中第一次到达的点，我们把环中的 dfs 第一次到达的点称为入点，此时我们直接让 1 号点所在环内其他的点跑 dfs，也就是 2、3 点，假设现在它们都跑出来了以自己根的子树内的 \(f\) 数组。

实际情况其实环内除入点之外的每个点为根的子树都分别可能顺时针和逆时针各走一遍走到入点。

所以我们枚举每个点作为起点分别向右和向左各走一次，每一次维护出一个数组 \(A_i\) 表示当前情况下以 \(i\) 为结尾的路径方案数。

每次走到一个新点 \(x\)，转移如下：\(A' = A+f_x+\sum_{i=x+1}^n A_i\)。

这样时间复杂度不对。如上图，最后得到的 \(A\) 数组如下：

\[\begin{aligned}
A =& f_2+\sum_{i=3}^n f_{2,i} （以 2 为起点向右走）
\\ &+ f_2 （以 2 为起点向左走）
\\ &+ f_3+\sum_{i=2}^n f_{2,j} （以 3 为起点向左走）
\\ &+ f_3 （以 3 为起点向右走）
\\ =& f_2+f_3+\sum_{i=3}^n f_{2,i} （把向左走的合到一起）
\\ &+ f_2+f_3+\sum_{i=2}^n f_{2,j} （把向右走的合到一起）
\end{aligned}\]

容易发现对入点的贡献就是顺时针走一遍逆时针走一遍，减去（重复的）每颗子树原本的贡献

那么我们看做把 1、2 的连边断开，从 2 -> 3 -> 1 的路径进行一次上述转移；

反过来，从 3 -> 2 -> 1 的路径再进行一次转移。

所以总体思路就是，每遇到一个环把环上其他点的子树先跑出来，然后顺时针逆时针各跑一遍维护环中的子树对入点的贡献。

发现很简单，\(n^3\) 就做完了，但 lxyt 说的好：“\(500^3\) 很难过啊”，Ratio 也说得好：“\(500^3\) 除非你常数极小”。

考虑优化，我们称以 \(i\) 为终点的递减路径的方案数为 \(i\) 的方案数。

每次更新 \(u\) 点的方案时，会计算 \(u\) 点所有的子节点 \(v\) 的子树内 所有大于 \(u\) 的点的方案数的总和，发现其实这就是简单区间求和，可以线段树维护。

• 而是先整体考虑树的转移：

  对于每一个叶子点开一棵线段树（动态开点），那么我们每次从一个 \(v\) 点回溯到父节点 \(u\) 并更新它时，直接区间求和求出 \(v\) 子树内对 \(u\) 的贡献，将这一贡献单点更新到 \(u\) 的线段树上，并合并 \(v\) 的线段树到 \(u\) 上。

• 环的转移：

  按暴力思路顺时针走一遍，把走过的点的线段树以及新产生的贡献合并到一个新线段树上，最后把对入点的贡献加到入点的线段树上并把整颗线段树合并上去；

  逆时针的时候，为了避免重复，我们照样开上述一颗线段树 \(x\)，再额外开一颗线段树只把 \(x\) 这颗线段树上在转移过程中新产生的贡献加上，而不加每颗子树原本就有的线段树的部分。

单点更新和区间查询单次 \(log\)，每次 dfs 共 \(O(n\log n)\)，整体复杂度为 \(O(n^2 \log n)\)。

code：

看懂思路的话，代码也会很好写啦。

#include<bits/stdc++.h>
#define int long long
#define lson ls[rt]
#define rson rs[rt]
#define Aqrfre(x, y) freopen(#x ".in", "r", stdin),freopen(#y ".out", "w", stdout)
#define mp make_pair
#define Type int
#define qr(x) x=read()
typedef __int128 INT;
typedef long long ll;
using namespace std;

inline Type read(){
    char c=getchar(); Type x=0, f=1;
    while(!isdigit(c)) (c=='-'?f=-1:f=1), c=getchar();
    while(isdigit(c)) x=(x<<1)+(x<<3)+(c^48), c=getchar();
    return x*f;
}

const int N = 505;
const int M = 5e6;
const int mod = 998244353;

int n, m, tot, dis[N][N]; ll res;
vector<int>to[N], belong[N]; bool beA[N][N];

int top, th, s[N], bcc, low[N], dfn[N];
vector<int>BCC[N]; int sz[N];
inline void tarjan(int x, int p){
    s[++top] = x;
    low[x] = dfn[x] = ++th;
    for(int y : to[x]){
        if(!dfn[y]){
            tarjan(y, x);
            low[x] = min(low[x], low[y]);
            if(low[y] == dfn[x]){
                ++bcc;
                do{ BCC[bcc].emplace_back(s[top]); sz[bcc]++;
                    belong[s[top]].emplace_back(bcc);
                    beA[s[top]][bcc] = true;
                }while(s[top--] != y);

                BCC[bcc].emplace_back(x); sz[bcc]++;
                belong[x].emplace_back(bcc);
                beA[x][bcc] = true;
            }
        }
        else low[x] = min(low[x], dfn[y]);
    }
}

vector<int>tw[N][N];
ll v[M]; int rtot, ls[M], rs[M], root[M];
inline void pushup(int rt){
    v[rt] = (ll)(v[lson] + v[rson]) % mod;
} 

inline void update(int &rt, int l, int r, int pos, int val){
    if(!rt) rt = ++rtot;
    if(l == r){
        (v[rt] += val) %= mod;
        return;
    }

    int mid = (l + r) >> 1;
    if(pos <= mid) update(lson, l, mid, pos, val);
    else update(rson, mid+1, r, pos, val);

    pushup(rt);
}

inline int merge(int x, int y, int l, int r){
    if(!x or !y) return x + y;
    if(l == r){
        (v[x] += v[y]) %= mod;
        return x;
    }
    int mid = (l + r) >> 1;
    ls[x] = merge(ls[x], ls[y], l, mid);
    rs[x] = merge(rs[x], rs[y], mid+1, r);

    pushup(x); return x;
}

inline void mcpy(int &x, int y, int l, int r){
    if(!y) return;
    x = ++rtot;
    v[x] = v[y];
    if(l == r) return;

    int mid = (l + r) >> 1;
    mcpy(ls[x], ls[y], l, mid);
    mcpy(rs[x], rs[y], mid+1, r);
}

inline void mergeAdd(int &x, int y, int l, int r){
    if(!y) return;
    if(!x) x = (++rtot);
    if(l == r){
        (v[x] += v[y]) %= mod;
        return;
    }
    int mid = (l + r) >> 1;
    mergeAdd(ls[x], ls[y], l, mid);
    mergeAdd(rs[x], rs[y], mid+1, r);

    pushup(x); return;
}

inline int query(int rt, int l, int r, int pos){
    if(!rt) return 0;
    if(l >= pos){
        return v[rt] % mod;
    }
    int mid = (l + r) >> 1, res = 0;
    if(mid >= pos) res = query(lson, l, mid, pos);
    (res += query(rson, mid+1, r, pos)) %= mod;

    return res;
}

inline void watch(int rt, int l, int r){
    int mid = l + r >> 1;
    if(ls[rt]) watch(lson, l, mid);
    if(rs[rt]) watch(rson, mid+1, r);
    if(rt) cout<<l<<" "<<r<<' '<<v[rt]<<'\n';
}

inline int qpos(int rt, int l, int r, int pos){
    if(l == r) return v[rt] % mod;
    int mid = (l + r) >> 1;
    if(mid >= pos) return qpos(lson, l, mid, pos);
    else return qpos(rson, mid+1, r, pos);
}

int ned, tem;
inline void dp(int x, int p, int goal, int whi, int op){
    if(x == goal) return;
    int num = 0;
    for(int y : tw[whi][x]){
        if(y == p) continue;

        num = query(root[ned], 1, n, y);

        mergeAdd(root[ned], root[y], 1, n);
        update(root[ned], 1, n, y, num);

        if(op == 1){
            update(root[tem], 1, n, y, num);
        }

        if(y == goal) break;
        dp(y, x, goal, whi, op);
    }
}

bool vis[N], flag[N];
inline void dfs(int x, int p, int bel){
    update(root[x], 1, n, x, 1);
    for(int whi : belong[x]){
        if(whi == bel) continue;
        if(flag[whi]) continue;
        flag[whi] = true;

        if(sz[whi] == 2){
            int num = 0;
            for(int y : tw[whi][x]){
                if(y == p or vis[y]) continue;
                vis[y] = true;
                dfs(y, x, whi);
                root[x] = merge(root[x], root[y], 1, n);
                num += query(root[y], 1, n, x);
            }
            update(root[x], 1, n, x, num);

            continue;
        }

        for(int i : BCC[whi]){
            if(x == i) continue;
            vis[i] = true;
            dfs(i, 0, whi);
        }

        int a = 0, b = 0;
        for(int i : tw[whi][x]){
            if(a) b = i;
            else a = i;
        }

        ned++; mcpy(root[ned], root[a], 1, n);
        dp(a, x, b, whi, 0);
        mergeAdd(root[x], root[ned], 1, n);
        update(root[x], 1, n, x, query(root[ned], 1, n, x));

        ned++; mcpy(root[ned], root[b], 1, n); tem = ned + 1;
        dp(b, x, a, whi, 1);
        mergeAdd(root[x], root[tem], 1, n);
        update(root[x], 1, n, x, query(root[tem], 1, n, x));
    }
}

inline void clean(){
    ned = max(ned, tem);
    fill(root+1, root+1+ned, 0);
    fill(flag, flag+1+n, 0);
    fill(vis, vis+1+n, 0);
    fill(ls, ls+1+rtot, 0);
    fill(rs, rs+1+rtot, 0);
    fill(v, v+1+rtot, 0);
    rtot = 0; ned = n;
}

signed main(){ //algebra
    Aqrfre(algebra, algebra);

    qr(n), qr(m); ned = n;
    for(int i=1; i<=m; i++){
        int qr(x), qr(y);
        dis[x][y] = dis[y][x] = 1;
        to[x].emplace_back(y);
        to[y].emplace_back(x);
    }
    for(int i=1; i<=n; i++)
        if(!dfn[i]) tarjan(i, 0);

    for(int i=1; i<=bcc; i++)
        for(int x : BCC[i])
            for(int y : BCC[i]){
                if(x == y or !dis[x][y]) continue;
                tw[i][x].emplace_back(y);
            }

    int la = 0;
    for(int i=1; i<=n; i++){
        clean(); dfs(i, 0, 0);
        (res += qpos(root[i], 1, n, i)) %= mod;
    }

    cout<<res<<"\n";

    return 0;
}