用牛顿-拉弗森法定义平方根函数（Newton-Raphson method Square Root Python）

牛顿法（Newton’s method）又称为牛顿-拉弗森法（Newton-Raphson method），是一种近似求解实数方程式的方法。（注：Joseph Raphson在1690年出版的《一般方程分析》中提出了后来被称为“牛顿-拉弗森法”的数学方法，牛顿于1671年写成的著作《流数法》中亦包括了这个方法，但该书在1736年才出版。）

之前的一篇博客中提到的二分法可以求解方根（用二分法定义平方根函数），而使用牛顿迭代法可以更快地解出方根。现在，人们使用的计算器里面大多数都是运用的牛顿迭代法。

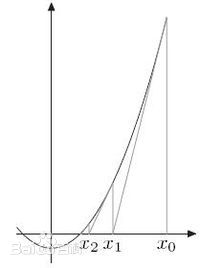
假设n=x²，现在需要求n的方根，n=x²亦即x²-n=0，把它转换成方程式f(x)=x²-n，如上图所示。

选取作为求解方根的初始近似值，过点作切线T，T的方程为，求出T与x轴交点的横坐标，称x₁为n方根的一次近似值。

过点再作切线，并求得该切线与x轴交点的横坐标，称为n方根的二次近似值。

以此类推，得到牛顿法的迭代公式： （注：f'(x_n)是导数，这里也就是切线的斜率，数值是2*x_n）。

猜测值在经过多次迭代后会越来越接近曲线的根，用数学术语来说就是，这个方程式在的时候收敛，故能求得近似n方根的值。

总的图示如下：

代码如下：

def sqrt_NR(n):
    '''为了方便起见，先假设n为正数'''
    guess=n/2  # 设置初始猜测值为n的一半
    diff=guess**2-n  # f(Xn)
    count=1  # 设置猜测次数起始值为1
    while abs(diff)>0.001 and count<100: # 当猜测值的平方和n本身的差值无限接近误差值时，循环才会停止；同时设置猜测次数不超过100次
        guess=guess-diff/(2*guess)  # 根据牛顿法的迭代公式Xn+1=Xn-f(Xn)/f'(Xn)，将上一次的猜测值减去f(Xn)/导数的值赋予新的猜测值
        diff=guess**2-n  # 更新f(Xn)
        count+=1  # 猜测次数每次增加1
    return guess

 

调用此函数试一下：

print(sqrt_NR(8))

运行结果如下：

2.8284313725490198

二分法和牛顿法对比：

把这两个函数的eplison都设置为0.01，增加显示count

运行：

print(“二分法： ", sqrt_bi(8))
print("牛顿法： ", sqrt_NR(8))

结果如下：

二分法：    (2.828369140625, 15)

牛顿法：    (2.8284313725490198, 4)

是不是牛顿法比二分法快多了？

参考：麻省理工学院公开课：计算机科学及编程导论  （第6课）