主成分分析(PCA)是最常见的降维算法。

　　在PCA 中，我们要做的是找到一个方向向量（Vector direction），当我们把所有的数据
都投射到该向量上时，我们希望投射平均均方误差能尽可能地小。方向向量是一个经过原点
的向量，而投射误差是从特征向量向该方向向量作垂线的长度。

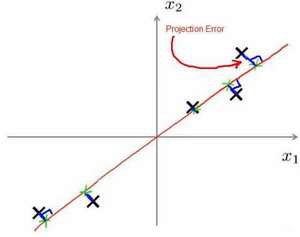
　　下面给出主成分分析问题的描述：
问题是要将

吴恩达机器学习笔记49-主成分分析问题（Principal Component Analysis Problem Formulation）的更多相关文章

  1. 吴恩达机器学习笔记19-过拟合的问题（The Problem of Overfitting）

    到现在为止,我们已经学习了几种不同的学习算法,包括线性回归和逻辑回归,它们能够有效地解决许多问题,但是当将它们应用到某些特定的机器学习应用时,会遇到过拟合(over-fitting)的问题,可能会导致 ...

  2. [吴恩达机器学习笔记]14降维3-4PCA算法原理

    14.降维 觉得有用的话,欢迎一起讨论相互学习~Follow Me 14.3主成分分析原理Proncipal Component Analysis Problem Formulation 主成分分析( ...

  3. 吴恩达机器学习笔记（六） —— 支持向量机SVM

    主要内容: 一.损失函数 二.决策边界 三.Kernel 四.使用SVM (有关SVM数学解释:机器学习笔记(八)震惊!支持向量机(SVM)居然是这种机) 一.损失函数 二.决策边界 对于: 当C非常 ...

  4. Machine Learning——吴恩达机器学习笔记（酷

    [1] ML Introduction a. supervised learning & unsupervised learning 监督学习:从给定的训练数据集中学习出一个函数(模型参数), ...

  5. 吴恩达机器学习笔记（八） —— 降维与主成分分析法(PCA)

    主要内容: 一.降维与PCA 二.PCA算法过程 三.PCA之恢复 四.如何选取维数K 五.PCA的作用与适用场合 一.降维与PCA 1.所谓降维,就是将数据由原来的n个特征(feature)缩减为k ...

  6. [吴恩达机器学习笔记]14降维5-7重建压缩表示/主成分数量选取/PCA应用误区

    14.降维 觉得有用的话,欢迎一起讨论相互学习~Follow Me 14.5重建压缩表示 Reconstruction from Compressed Representation 使用PCA,可以把 ...

  7. [吴恩达机器学习笔记]12支持向量机5SVM参数细节

    12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.5 SVM参数细节 标记点选取 标记点(landma ...

  8. [吴恩达机器学习笔记]12支持向量机3SVM大间距分类的数学解释

    12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.3 大间距分类背后的数学原理- Mathematic ...

  9. [吴恩达机器学习笔记]12支持向量机2 SVM的正则化参数和决策间距

    12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.2 大间距的直观理解- Large Margin I ...

  10. [吴恩达机器学习笔记]12支持向量机1从逻辑回归到SVM/SVM的损失函数

    12.支持向量机 觉得有用的话,欢迎一起讨论相互学习~Follow Me 参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广 12.1 SVM损失函数 从逻辑回归到支持向量机 为了描述 ...

随机推荐

  1. C#多线程--信号量（Semaphore）[z]

    百度百科:Semaphore,是负责协调各个线程, 以保证它们能够正确.合理的使用公共资源.也是操作系统中用于控制进程同步互斥的量. Semaphore常用的方法有两个WaitOne()和Releas ...

  2. ROS零门槛学渣教程系列（二十）——ROSJAVA和Android

    ros wiki地址:http://wiki.ros.org/android 第一步:安装JDK (参考博文:https://blog.csdn.net/Hong_A/article/details/ ...

  3. 分析easyswoole3.0源码，体验es3（三）

    demo在手,总得去试试看效果吧.我们先把默认的服务改成webserver,并且添加数据库的配置. 建立数据库,github里面有相关内容 CREATE TABLE `user_list` ( `us ...

  4. skynet记录7：服务（c和lua）

    稍后填坑 1.c服务的写法(第一个服务logger分析) 2.lua服务的写法(第二个服务bootstrap分析) 3.snlua包装模块

  5. Windows PowerShell基本语法及常用命令

    PowerShell常用命令: 一 Get类 1.Get-Command : 得到所有PowerShell命令,获取有关 cmdlet 以及有关 Windows PowerShell 命令的其他元素的 ...

  6. FPGA學習筆記（肆）--- Star Test Bench Template Writer

    上一篇testbench我自己也沒怎麽搞懂,再來一篇學習特權同學的方法. 課程:Lesson 7 BJ EPM240学习板实验1——分频计数实验 鏈接:https://www.youtube.com/ ...

  7. 安卓adb工具的安装方法

    adb是Android的一个很重要的调试工具,熟练掌握后可实现很多功能,比如有些手机的解锁.ROOT就会用到adb工具.可很多朋友都说不会安装,今天就从最开始的安装方法说起. adb工具其实不用安装, ...

  8. experiment 3

    #include <stdio.h> int main() { int number, max, min, n; n=; printf("请输入%d个数: ", n); ...

  9. Springboot & Mybatis 构建restful 服务五

    Springboot & Mybatis 构建restful 服务五 1 前置条件 成功执行完Springboot & Mybatis 构建restful 服务四 2 restful ...

  10. JQUERY-自定义插件-ajax-跨域访问

    正课: 1. ***自定义插件: 2. Ajax 3. *****跨域访问: 1. ***自定义插件: 前提: 已经用html,css,js实现了 2种风格: 1. jQueryUI侵入式: 1. c ...