python 平衡二叉树实现

平衡二叉树：

　　在上一节二叉树的基础上我们实现，如何将生成平衡的二叉树

　　所谓平衡二叉树：

　　　　我自己定义就是：任何一个节点的左高度和右高度的差的绝对值都小于2

　　　　如图所示，此时a的左高度等于3，有高度等于1，差值为2，属于不平衡中的左偏

　　

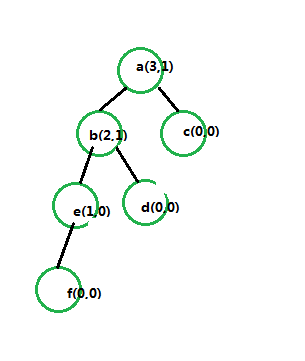
　　此时的处理办法就是：

　　　　将不平衡的元素的左枝的最右节点变为当前节点，

　　　　此时分两种情况：

　　　　　一、左枝有最右节点

　　　　　　将最右节点的左枝赋予其父节点的右枝

　　　　　二、左枝没有最右节点，

　　　　　　直接将左枝节点做父级节点，父级节点做其右枝

　　　　　　

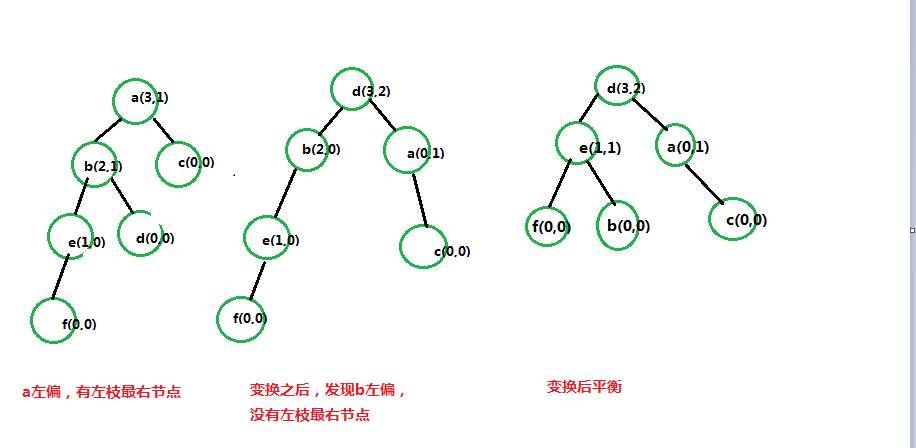
　　如图所示，图更清楚些。

可能会有疑问，为什么这样变换？

　　　　假定a左偏，就需要一个比a小的最少一个值d(因为d唯一 一个是比a小，而且比a的左枝所有数都大的值)做父集结点，a做d的右枝，这样在最上面的d节点就平衡了。

　　　　我们可以反证一下：

　　　　　如果不是d是另一个数假设为h，此时h做父节点，a做父节点的右节点

　　　　  因为a在h右边，所以 a > h

　　　　  因为b,e,d,f都是h的左枝，所以  h>d>b>e>f

　　　　  所以 a>h>d>b>e>f

　　　　  所以在不加入新节点的情况下，就只能是d　　　　

左偏和右偏是一样的，可以完全镜像过来就ok了

处理了所有节点 的左偏和右偏使整个二叉树平衡，这就是平衡二叉树的基本思想

代码实现：

# -*- coding:utf-8  -*-
# 日期：2018/6/12 8:37
# Author:小鼠标

# 节点对象
class Node:
    def __init__(self):
        self.left_children = None
        self.left_height = 0
        self.right_children = None
        self.right_height = 0
        self.value = None

# 二叉树对象
class tree:
    def __init__(self):
        self.root = False
        self.front_list = []
        self.middle_list = []
        self.after_list = []
    # 生成二叉树
    def create_tree(self,n=0,l=[]):
        if l == []:
            print("传入的列表为空")
            return
        if n > len(l)-1:
            print("二叉树生成")
            return
        node = Node()
        node.value = l[n]
        if not self.root:
           self.root = node
           self.list = l
        else:
            self.add(self.root,node)
        self.create_tree(n+1,l)
    # 添加节点
    def add(self,parent,new_node):
        if new_node.value > parent.value:
            # 插入值比父亲值大，所以在父节点右边
            if parent.right_children == None:
                parent.right_children = new_node
                # 新插入节点的父亲节点的高度值为1，也就是子高度值0+1
                parent.right_height = 1
                # 插入值后 从下到上更新节点的height
            else:
                self.add(parent.right_children,new_node)
                # 父亲节点的右高度等于右孩子，左右高度中较大的值 + 1
                parent.right_height = max(parent.right_children.right_height, parent.right_children.left_height) + 1
                # ======= 此处开始判断平衡二叉树=======
                # 右边高度大于左边高度 属于右偏
                if parent.right_height - parent.left_height >= 2:
                    self.right_avertence(parent)
        else:
            # 插入值比父亲值小，所以在父节点左边
            if parent.left_children == None:
                parent.left_children = new_node
                parent.left_height = 1
            else:
                self.add(parent.left_children,new_node)
                parent.left_height = max(parent.left_children.right_height, parent.left_children.left_height) + 1
                # ======= 此处开始判断平衡二叉树=======
                # 左边高度大于右边高度 属于左偏
                if parent.left_height - parent.right_height >= 2:
                    self.left_avertence(parent)
    # 更新当前节点下的所有节点的高度
    def update_height(self,node):
        # 初始化节点高度值为0
        node.left_height = 0
        node.right_height = 0
        # 是否到最底层的一个
        if node.left_children == None and node.right_children == None:
            return
        else:
            if node.left_children:
                self.update_height(node.left_children)
                # 当前节点的高度等于左右子节点高度的较大值 + 1
                node.left_height = max(node.left_children.left_height,node.left_children.right_height) + 1
            if node.right_children:
                self.update_height(node.right_children)
                # 当前节点的高度等于左右子节点高度的较大值 + 1
                node.right_height = max(node.right_children.left_height, node.right_children.right_height) + 1
            # 检查是否仍有不平衡
            if node.left_height - node.right_height >= 2:
                self.left_avertence(node)
            elif node.left_height - node.right_height <= -2:
                self.right_avertence(node)

    def right_avertence(self,node):
        # 右偏 就将当前节点的最左节点做父亲
        new_code = Node()
        new_code.value = node.value
        new_code.left_children = node.left_children
        best_left = self.best_left_right(node.right_children)
        v = node.value
        # 返回的对象本身,
        if best_left == node.right_children and best_left.left_children == None:
            # 说明当前节点没有有节点
            node.value = best_left.value
            node.right_children = best_left.right_children
        else:
            node.value = best_left.left_children.value
            best_left.left_children = best_left.left_children.right_children
        node.left_children = new_code
        self.update_height(node)

    # 处理左偏情况
    def left_avertence(self,node):
        new_code = Node()
        new_code.value = node.value
        new_code.right_children = node.right_children
        best_right = self.best_left_right(node.left_children,1)
        v = node.value
        # 返回的对象本身,
        if best_right == node.left_children and best_right.right_children == None:
            # 说明当前节点没有有节点
            node.value = best_right.value
            node.left_children = best_right.left_children
        else:
            node.value = best_right.right_children.value
            best_right.right_children = best_right.right_children.left_children
        node.right_children = new_code
        self.update_height(node)
    # 返回node节点最左（右）子孙的父级
    def best_left_right(self,node,type=0):
        # type=0 默认找最左子孙
        if type == 0:
            if node.left_children == None:
                return node
            elif node.left_children.left_children == None:
                return node
            else:
                return self.best_left_right(node.left_children,type)
        else:
            if node.right_children == None:
                return node
            elif node.right_children.right_children == None:
                return node
            else:
                return self.best_left_right(node.right_children,type)
    # 前序(先中再左最后右)
    def front(self,node=None):
        if node == None:
            self.front_list = []
            node = self.root
        # 输出当前节点
        self.front_list.append(node.value)
        # 先判断左枝
        if not node.left_children == None:
            self.front(node.left_children)
        # 再判断右枝
        if not node.right_children == None:
            self.front(node.right_children)
        # 返回最终结果
        return self.front_list
    # 中序(先左再中最后右)
    def middle(self,node=None):
        if node == None:
            node = self.root
        # 先判断左枝
        if not node.left_children == None:
            self.middle(node.left_children)
        # 输出当前节点
        self.middle_list.append(node.value)
        # 再判断右枝
        if not node.right_children == None:
            self.middle(node.right_children)
        return self.middle_list
    # 后序(先左再右最后中)
    def after(self,node=None):
        if node == None:
            node = self.root
        # 先判断左枝
        if not node.left_children == None:
            self.after(node.left_children)
        # 再判断右枝
        if not node.right_children == None:
            self.after(node.right_children)
        self.after_list.append(node.value)
        return self.after_list
    # 节点删除
    def del_node(self,v,node=None):
        if node == None:
            node = self.root
            # 删除根节点
            if node.value == v:
                self.del_root(self.root)
                return
        # 删除当前节点的左节点
        if node.left_children:
            if node.left_children.value == v:
                self.del_left(node)
                return
        # 删除当前节点的右节点
        if node.right_children:
            if node.right_children.value == v:
                self.del_right(node)
                return
        if v > node.value:
            if node.right_children:
                self.del_node(v, node.right_children)
            else:
                print("删除的元素不存在")
        else:
            if node.left_children:
                self.del_node(v, node.left_children)
            else:
                print("删除的元素不存在")
    #删除当前节点的右节点
    def del_right(self,node):
        # 情况1 删除节点没有右枝
        if node.right_children.right_children == None:
            node.right_children = node.right_children.left_children
        else:
            best_left = self.best_left_right(node.right_children.right_children)
            # 表示右枝最左孙就是右枝本身
            if best_left == node.right_children.right_children and best_left.left_children == None:
                node.right_children.value = best_left.value
                node.right_children.right_children = best_left.right_children
            else:
                node.right_children.value = best_left.left_children.value
                best_left.left_children = best_left.left_children.right_children
    # 删除当前节点的左节点
    def del_left(self,node):
        # 情况1 删除节点没有右枝
        if node.left_children.right_children == None:
            node.left_children = node.left_children.left_children
        else:
            best_left = self.best_left_right(node.left_children.right_children)
            # 表示右枝最左子孙就是右枝本身
            if best_left == node.left_children.right_children and best_left.left_children == None:
                node.left_children.value = best_left.value
                node.left_children.right_children = best_left.right_children
            else:
                node.left_children.value = best_left.left_children.value
                best_left.left_children = best_left.left_children.right_children
    # 删除根节点
    def del_root(self,node):
        if node.right_children == None:
            if node.left_children == None:
                node.value = None
            else:
                self.root = node.left_children
        else:
            best_left = self.best_left_right(node.right_children)
            # 表示右枝最左子孙就是右枝本身
            if best_left == node.right_children and best_left.left_children == None:
                node.value = best_left.value
                node.right_children = best_left.right_children
            else:
                node.value = best_left.left_children.value
                best_left.left_children = best_left.left_children.right_children

    # 搜索
    def search(self,v,node=None):
        if node == None:
            node = self.root
        if node.value == v:
            return True
        if v > node.value:
            if not node.right_children == None:
                return self.search(v, node.right_children)
        else:
            if not node.left_children == None:
                return self.search(v, node.left_children)
        return False
if __name__ == '__main__':
    # 需要建立二叉树的列表
    list = [4, 6, 3, 1, 7, 9, 8, 5, 2]
    t = tree()
    t.create_tree(0,list)
    res = t.front()
    print('前序', res)

执行结果：

　　前序 [4, 2, 1, 3, 7, 6, 5, 9, 8]

　　通过前序可以画出二叉树

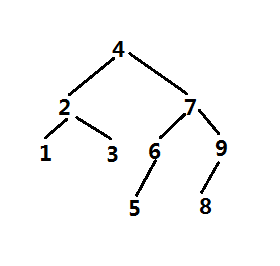
完美，哈哈。

这是我钻了两天才写出的代码，哈哈，努力还是有回报的，加油。

下一步就是代码优化了