Deep Learning Tutorial - Multilayer perceptron

Multilayer perceptron：多层感知器

本节实现两层网络（一个隐层）作为分类器实现手写数字分类。引入的内容：激活函数（双曲正切、L1和L2正则化）、Theano的共享变量、grad、floatX等。损失函数和错误率沿用了上一节的LogisticRegression类。本节没有使用反向传播来更新参数，用的依旧是损失函数对参数求导（梯度下降法）。网络隐层的激活函数为tanh，输出层即采用LogisticRegression。更新参数的机制：损失函数为LogisticRegression中的损失函数+两层网络的正则化的和，参数为两层分别的W和b。

要点如下：

1.初始化权重，众所周知在使用sigmoid激活函数时权重初始为零可能导致学习缓慢、隐层神经元的饱和。有许多方法初始化权重，文中给出：

当激活函数为双曲正切时 ：W取值为 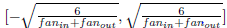 之间。

当激活函数为sigmoid时：W取值为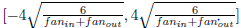：之间。

2.网络中的超参数一般来说不能用梯度下降法优化，严格地讲，找到这些参数的最优解不可行。首先，我们不能简单地独立的优化它们中的每一个参数，其次不能应用之前的梯度下降法，最后优化问题非凸很难找到局部最小值。一个好的解决办法是反向传播，由Yann LeCun提出的。

3.学习速率：简单的解决办法是设为定值，随着时间减小学习速率有时也很好，一个简单的法则是μ0/(1+d*t)，μ0为初始设置的速率，d称为衰减常数控制衰减速率（10e-3或更小），t为迭代周期数。

总体代码如下：

# coding=UTF-8
# 两层网络、sgd优化（非bp）、early-stopping策略
import os
import sys
import timeit
import numpy
import theano
import theano.tensor as T
from Logistic_sgd import LogisticRegression, load_data    #导入上一节的代码作为输出层

class HiddenLayer(object):                 #隐层类
    def __init__(self, rng, input, n_in, n_out, W=None, b=None, activation=T.tanh):
        self.input = input
        if W is None:
            W_values = numpy.asarray(     #W非初始化为零
                rng.uniform(
                    low=-numpy.sqrt(6. / (n_in + n_out)),
                    high=numpy.sqrt(6. / (n_in + n_out)),
                    size=(n_in, n_out)), dtype=theano.config.floatX)
            if activation == theano.tensor.nnet.sigmoid:
                W_values *= 4
            W = theano.shared(value=W_values, name='W', borrow=True)
        if b is None:                     #b初始化为零
            b_values = numpy.zeros((n_out), dtype=theano.config.floatX)
            b = theano.shared(value=b_values, name='b',borrow=True)
        self.W = W
        self.b = b
        lin_output = T.dot(input, self.W) + self.b
        self.output = (lin_output if activation is None else activation(lin_output))
        self.params = [self.W, self.b]

class MLP(object):     #输出层
    def __init__(self, rng, input, n_in, n_hidden, n_out):
        self.hiddenLayer = HiddenLayer(rng=rng, input=input, n_in=n_in, n_out=n_hidden, activation=T.tanh)
        self.logRegressionLayer = LogisticRegression(input=self.hiddenLayer.output, n_in=n_hidden, n_out=n_out)  #引入输出层
        self.L1 = (abs(self.hiddenLayer.W).sum()+ abs(self.logRegressionLayer.W).sum())
        self.L2_sqr = ((self.hiddenLayer.W ** 2).sum() + (self.logRegressionLayer.W ** 2).sum())  #L1，L2正则化
        self.negative_log_likelihood = (self.logRegressionLayer.negative_log_likelihood)
        self.errors = self.logRegressionLayer.errors
        self.params = self.hiddenLayer.params + self.logRegressionLayer.params     #参数包括隐层和输出层
        self.input = input

def test_mlp(learning_rate=0.01, L1_reg=0.00, L2_reg=0.0001, n_epochs=1000,
             dataset='data/mnist.pkl.gz', batch_size=20, n_hidden=500):
    datasets = load_data(dataset)
    train_set_x, train_set_y = datasets[0]
    valid_set_x, valid_set_y = datasets[1]
    test_set_x, test_set_y = datasets[2]
    n_train_batches = train_set_x.get_value(borrow=True).shape[0] / batch_size
    n_valid_batches = valid_set_x.get_value(borrow=True).shape[0] / batch_size
    n_test_batches = test_set_x.get_value(borrow=True).shape[0] / batch_size
    print '...building the model'
    index = T.lscalar()
    x = T.matrix('x')
    y = T.ivector('y')
    rng = numpy.random.RandomState(1234)       #随机数
    classifier = MLP(rng=rng, input=x, n_in=28 * 28, n_hidden=n_hidden, n_out=10)    #分类器
    cost = (classifier.negative_log_likelihood(y) + L1_reg * classifier.L1 + L2_reg * classifier.L2_sqr)  #损失函数
    test_model = theano.function(inputs=[index], outputs=classifier.errors(y), #测试模型
                                 givens={x: test_set_x[index * batch_size:(index + 1) * batch_size],
                                         y: test_set_y[index * batch_size:(index + 1) * batch_size]})
    validate_model = theano.function(inputs=[index], outputs=classifier.errors(y),  #验证模型
                                     givens={x: valid_set_x[index * batch_size:(index + 1) * batch_size],
                                             y: valid_set_y[index * batch_size:(index + 1) * batch_size]})
    gparams = [T.grad(cost, param) for param in classifier.params]
    updates = [(param, param - learning_rate * gparam) for param, gparam in zip(classifier.params, gparams)]
    train_model = theano.function(inputs=[index], outputs=cost, updates=updates,    #训练模型
                                  givens={x: train_set_x[index * batch_size: (index + 1) * batch_size],
                                          y: train_set_y[index * batch_size: (index + 1) * batch_size]})
    print '...training'
    patience = 10000    #early stopping策略
    patience_increase = 2
    improvement_threshold = 0.995
    validation_frequency = min(n_train_batches, patience / 2)
    best_validation_loss = numpy.inf
    best_iter = 0
    test_score = 0.
    start_time = timeit.default_timer()
    epoch = 0
    done_looping = False
    while (epoch < n_epochs) and (not done_looping):        #迭代优化过程（以下注释和上一节相同）
        epoch = epoch + 1
        for minibatch_index in xrange(n_train_batches):
            minibatch_avg_cost = train_model(minibatch_index)
            iter = (epoch - 1) * n_train_batches + minibatch_index
            if (iter + 1) % validation_frequency == 0:
                validation_losses = [validate_model(i) for i in xrange(n_valid_batches)]
                this_validation_loss = numpy.mean(validation_losses)
                print('epoch %i, minibatch %i / %i, validation error %f %%' % (
                epoch, minibatch_index + 1, n_train_batches, this_validation_loss * 100.))
                if this_validation_loss < best_validation_loss:
                    if (this_validation_loss < best_validation_loss * improvement_threshold):
                        patience = max(patience, iter * patience_increase)
                    best_validation_loss = this_validation_loss  #最优解对应的验证损失值
                    best_iter = iter                      #最优解对应的迭代次数
                    test_losses = [test_model(i) for i in xrange(n_test_batches)]
                    test_score = numpy.mean(test_losses)
                    print(('epoch %i, minibatch %i / %i, test error of''best model %f %%') % (
                    epoch, minibatch_index + 1, n_train_batches, test_score * 100.))
        if patience <= iter:
            done_looping = True
            break
    end_time = timeit.default_timer()
    print(
    ('Optimization compelete.Best validation scores of % %%''obtained at iteration %i,with test performance %f %%')
    % (best_validation_loss * 100., best_iter + 1, test_score * 100.))

if __name__ == '__main__':
    test_mlp()