three.js 曲线

上几篇说了three.js的曲线，这篇来郭先生来说说three.js曲线，在线案例点击郭先生的博客查看。

1. 了解three.js曲线

之前已经说了一些three.js的几何体，这篇说一说three.js曲线。曲线的种类主要分两种，二维曲线和三维曲线。下面整理了这些曲线

名称	参数
ArcCurve（弧线）	aX – 圆的中心的X坐标，默认值为0。aY – 圆的中心的Y坐标，默认值为0。aRadius – 圆的半径，默认值为1。aStartAngle – 以弧度来表示，从正X轴算起曲线开始的角度，默认值为0。aEndAngle – 以弧度来表示，从正X轴算起曲线终止的角度，默认值为2 x Math.PI。aClockwise – 圆是否按照顺时针方向来绘制，默认值为false。aRotation – 以弧度表示，圆从X轴正方向逆时针的旋转角度（可选），默认值为0。
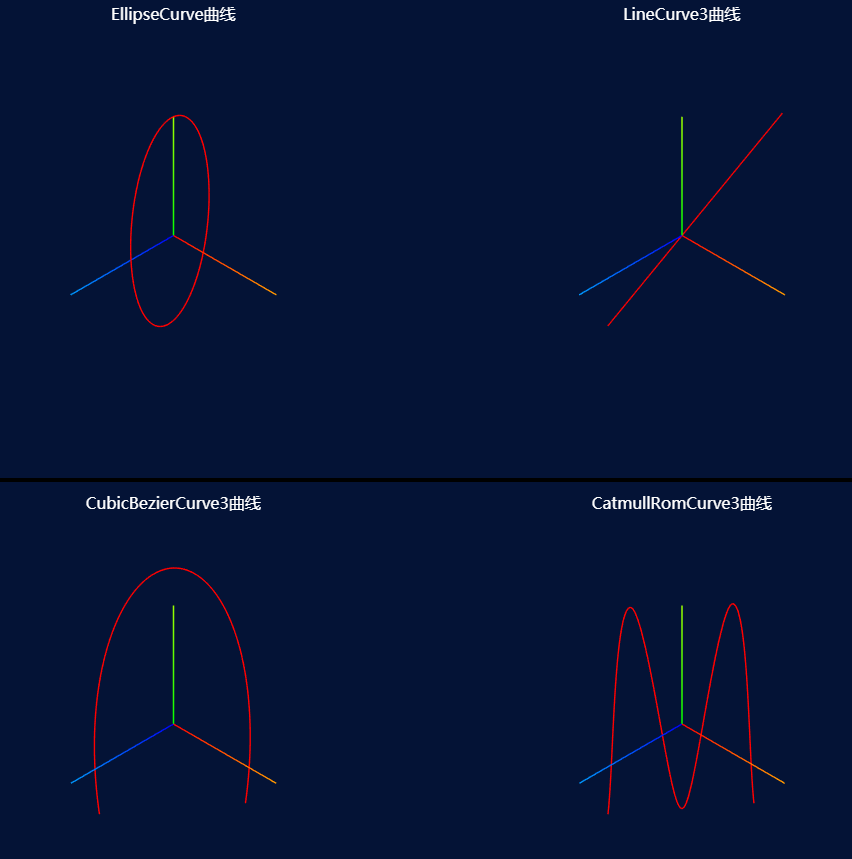
EllipseCurve（椭圆曲线）	aX – 椭圆的中心的X坐标，默认值为0。aY – 椭圆的中心的Y坐标，默认值为0。xRadius – X轴向上椭圆的半径，默认值为1。yRadius – Y轴向上椭圆的半径，默认值为1。aStartAngle – 以弧度来表示，从正X轴算起曲线开始的角度，默认值为0。aEndAngle – 以弧度来表示，从正X轴算起曲线终止的角度，默认值为2 x Math.PI。aClockwise – 椭圆是否按照顺时针方向来绘制，默认值为false。aRotation – 以弧度表示，椭圆从X轴正方向逆时针的旋转角度（可选），默认值为0。
LineCurve（二维线段曲线）	参数为起点v1:Vector2，和终点v2:Vector2
LineCurve3（三维线段曲线）	参数为起点v1:Vector3，和终点v2:Vector3
QuadraticBezierCurve（二维二次贝塞尔曲线）	参数为起点v1:Vector2，中间控制点a1:Vector2，终点v2:Vector2
QuadraticBezierCurve3（三维二次贝塞尔曲线）	参数为起点v1:Vector3，中间控制点a1:Vector3，终点v2:Vector3
CubicBezierCurve（二维三次贝塞尔曲线）	参数为起点v1:Vector2，中间控制点a1:Vector2，中间控制点a2:Vector2，终点v2:Vector2
CubicBezierCurve3（三维三次贝塞尔曲线）	参数为起点v1:Vector3，中间控制点a1:Vector3，中间控制点a2:Vector3，终点v2:Vector3
SplineCurve（样条曲线）	points – 定义曲线的Vector2点的数组。
CatmullRomCurve3（三维样条曲线）	points – Vector3点数组closed – 该曲线是否闭合，默认值为false。curveType – 曲线的类型，默认值为centripetal。tension – 曲线的张力，默认为0.5。

基本曲线主要是这些，ArcCurve和EllipseCurve是绘制圆和椭圆的，EllipseCurve是ArcCurve的基类，LineCurve和LineCurve3分别是二维和三维的曲线（数学曲线的定义包括直线），他们都是有起始点和终止点组成。QuadraticBezierCurve、QuadraticBezierCurve3、CubicBezierCurve和CubicBezierCurve3分别是二维和三维的二阶和三阶贝塞尔曲线，不知道贝塞尔曲线的人请移步至贝塞尔曲线，
SplineCurve和CatmullRomCurve3分别是二维和三维的样条曲线，它们使用Catmull-Rom算法，从一系列的点创建一条平滑的样条曲线。

2. 曲线的使用

这里我选取几个代表性的曲线

//椭圆曲线
var geometry = new THREE.Geometry();
var curve = new THREE.EllipseCurve(0,0,10,20);
var points = curve.getPoints(100);
geometry.setFromPoints(points);
var material = new THREE.LineBasicMaterial({color: 0xff0000});
var line = new THREE.Line(geometry, material);
scene.add(line);
//三维线段
var geometry = new THREE.Geometry();
var curve = new THREE.LineCurve3(new THREE.Vector3(10, 20, 10), new THREE.Vector3(-10, -20, -10));
var points = curve.getPoints(100);
geometry.setFromPoints(points);
var material = new THREE.LineBasicMaterial({color: 0xff0000});
var line = new THREE.Line(geometry, material);
scene.add(line);
//三维三阶贝塞尔曲线
var geometry = new THREE.Geometry();
var curve = new THREE.CubicBezierCurve3(new THREE.Vector3(-10, -20, -10), new THREE.Vector3(-10, 40, -10), new THREE.Vector3(10, 40, 10), new THREE.Vector3(10, -20, 10));
var points = curve.getPoints(100);
geometry.setFromPoints(points);
var material = new THREE.LineBasicMaterial({color: 0xff0000});
var line = new THREE.Line(geometry, material);
scene.add(line);
//三维样条曲线
var geometry = new THREE.Geometry();
var curve = new THREE.CatmullRomCurve3([new THREE.Vector3( -10, -20, -10 ),new THREE.Vector3( -5, 20, -5 ),new THREE.Vector3( 0, -20, 0 ),new THREE.Vector3( 5, 20, 5 ),new THREE.Vector3( 10, -20, 10 )]);
var points = curve.getPoints(100);
geometry.setFromPoints(points);
var material = new THREE.LineBasicMaterial({color: 0xff0000});
var line = new THREE.Line(geometry, material);
scene.add(line);

如下图

转载请注明地址：郭先生的博客