【题解】CIRU - The area of the union of circles [SP8073] \ 圆的面积并 [Bzoj2178]

传送门：

【题目描述】

给出 \(n\) 个圆的圆心坐标 \((x,y)\) 和半径 \(r\)，求它们覆盖的总面积。

【输入】

第一行一个整数 \(n\)，表示一共有 \(n\) 个圆，接下来 \(n\) 行每行三个整数 \(x,y,r\) 。

【输出】

答案保留三位小数。

【样例】

样例输入：
3
0 0 1
0 0 1
100 100 1
样例输出：
6.283

【数据范围】

\(100 \%:\) \(1 \leqslant n \leqslant 1000,\) \(|x|,|y| \leqslant 1000,\) \(0 \leqslant r \leqslant 1000\)

【分析】

【计算几何全家桶】

圆面积并的板题。

【前置芝士】

自适应辛普森积分 （乱搞）。

虽然不知道积分是什么东西，但老师说只要背了公式而且会用它求面积就可以了：\(ans(l,r)=\frac{(r-l)(F_l+4F_{mid}+F_r)}{6}\) 。

当计算平面图形面积时，\(F_Y\) 就是直线 \(y=Y\) 穿过图形的部分的长度。

例：一个底为 \(a\)，高为 \(h\) 的三角形面积可表示为： \(S=\frac{h*(a+4*\frac{a}{2}+0)}{6}=\frac{a*h}{2}\) 。如下图，\(r-l=h,F_l=a,F_{mid}=\frac{a}{2},F_r=0\)：

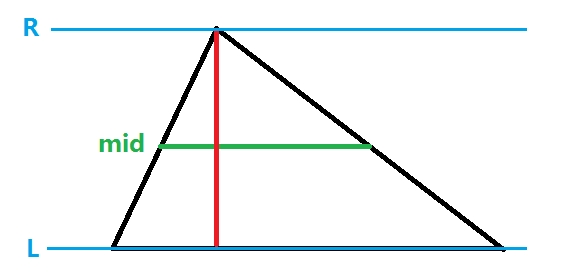
（另外，当计算立体图形体积时，\(F_Y\) 就是平面 \(z=Y\) 穿过图形的部分的面积。例：一个半径为 \(r\) 的球体积可表示为： \(V=\frac{2r*(0+4\pi r^2+0)}{6}=\frac{4\pi r^3}{3}\) ）

但并不是所有的图形都可以这样子做，比如在求圆面积时就会出问题（设半径为 \(r\)）： \(S=\frac{2r*(0+4*2r+0)}{6}=\frac{4 r^2}{3} \neq \pi r^2\) 。

这时候就需要用到自适应辛普森法：分别用公式出 \(ans(l,mid)\) 和 \(ans(mid,r)\)，若二者之和与 \(ans(l,r)\) 的差值小于 \(eps\)，则返回 \(ans(l,r)\)，否则递归求解 \((l,mid)\) 与 \((mid,r)\) 再加起来。

代码如下：

#define LD double
#define Rd register LD
inline LD F(Rd Y){return ???;}//视情况而定
inline LD Simpson(Rd L,Rd R){return (R-L)*(F(L)+4.0*F((L+R)*0.5)+F(R))/6.0;}//套公式
inline LD sakura(Rd L,Rd R,Rd now){//求解ans(L,R)
    Rd mid=(L+R)*0.5,FL=Simpson(L,mid),FR=Simpson(mid,R);//先用公式求左右两边
    if(!dcmp(now-FL-FR))return now;//满足精度要求
    return sakura(L,mid,FL)+sakura(mid,R,FR);//递归求解并求和
}

【问题求解】

回到这道题，求出最靠边上的两端点 \(Y_{min},Y_{max}\) 直接递归求解即可，至于上面的 \(F\) 函数可以暴力枚举所有圆求交弦，然后对其排序做线段覆盖。

注意精度要调好，\(\text{Bzoj}\) 需要 \(1e\!-\!13\)，\(\text{SPOJ}\) 需要 \(1e\!-\!7\) 。

时间复杂度： \(O( nlogn \times\) 玄学 \()\) 。其中 “玄学” 为 \(F\) 函数调用次数。

【优化】

只是单纯地求解 \((Y_{min},Y_{max})\) 会被 \(\text{Bzoj}\) 的【变态毒瘤数据】卡掉，\(\text{SPOJ}\) 也过不了。

为什么？

如果有 \(1\) 个孤零零的圆在最上面，\(999\) 个圆堆在最下面，最后算出来误差会非常大，所以要分段处理，即将所有圆划分为若干个联通块分别求解（可以将每个圆的上下端点连起来跑线段覆盖），这样子误差会小一些。

此时【变态毒瘤数据】成功地算了出来，但花了 \(30s\)，考虑对 \(F\) 函数进行记忆化，再经过一波卡常，本机 \(10.6s\)，交上去刚好卡过。

【再优化】

那么，连【八聚氧】都救不了的 \(\text{SPOJ}\) 又该怎么办呢？

提前预处理出大圆包含小圆的情况（把被包含的小圆删掉），大大减小 \(nlogn\) 部分的消耗。

呼呼，终于过了

【Code】

#include<algorithm>
#include<cstdio>
#include<cmath>
#include<map>
#define LD double
#define LL long long
#define Re register int
#define Rd register LD
#define Vector Point
using namespace std;
const int N=2003;
const LD eps=1e-13;
int n,m;map<LD,LD>vis;
inline int dcmp(Rd a){return a<-eps?-1:(a>eps?1:0);}
struct Point{
    LD x,y;Point(LD X=0,LD Y=0){x=X,y=Y;}
    inline void in(){scanf("%lf%lf",&x,&y);}
};
struct Segment{
    LD L,R;Segment(LD l=0,LD r=0){L=l,R=r;}
    inline bool operator<(Segment O)const{return L!=O.L?L<O.L:R<O.R;}
}Seg[N];
struct Circle{
    LD x,y,r,L,R,D,U;
    inline void in(){scanf("%lf%lf%lf",&x,&y,&r),L=x-r,R=x+r,D=y-r,U=y+r;}
    inline bool operator<(Circle B)const{return D<B.D;}//按下端点排序
}C[N],C_[N];
inline bool cmp(Circle A,Circle B){return A.r<B.r;}//按半径排序
inline LD dis(Circle A,Circle B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}
inline LD SS(Rd x){return x*x;}
inline LD F(Rd Y){
    if(vis[Y])return vis[Y];//记忆化
    Re t=0;Rd ans=0;
    for(Re i=1;i<=n;++i)
        if(dcmp(Y-C[i].D)>0&&dcmp(Y-C[i].U)<0){//如果直线穿过了该圆
            Rd tmp=sqrt(SS(C[i].r)-SS(C[i].y-Y));//勾股定理求交弦
            if(dcmp(tmp)>0)Seg[++t]=Segment(C[i].x-tmp,C[i].x+tmp);
        }
    if(!t)return 0.0;
    sort(Seg+1,Seg+t+1);
    for(Re i=1,j;i<=t;i=j+1){
        Rd L=Seg[i].L,R=Seg[i].R;j=i;
        while(j<t&&Seg[j+1].L<=R)++j,R=max(R,Seg[j].R);
        ans+=R-L;
    }
    return vis[Y]=ans;
}
inline LD Simpson(Rd L,Rd R){return (R-L)*(F(L)+4.0*F((L+R)*0.5)+F(R))/6.0;}//【辛普森公式】
inline LD sakura(Rd L,Rd R,Rd now){//【自适应】
    Rd mid=(L+R)*0.5,FL=Simpson(L,mid),FR=Simpson(mid,R);
    if(!dcmp(now-FL-FR))return now;
    return sakura(L,mid,FL)+sakura(mid,R,FR);
}
LD ans;
int main(){
//  freopen("789.txt","r",stdin);
    scanf("%d",&m);
    for(Re i=1;i<=m;++i)C_[i].in();
    sort(C_+1,C_+m+1,cmp),C[++n]=C_[m];//按半径大小排序
    for(Re i=m-1;i>=1;--i){//【大圆吃小圆】从大圆向小圆枚举
        Re flag=1;
        for(Re j=1;j<=n&&flag;++j)
            if(dcmp(C_[i].r-C[j].r+dis(C_[i],C[j]))<=0)flag=0;//小r+大r <= dis，则说明小圆C_[i]被包含了在了C[j]以内
        if(flag)C[++n]=C_[i];//C_[i]没有被大圆包含
    }
    sort(C+1,C+n+1);
    for(Re i=1,j;i<=n;i=j+1){//【分段处理】每个联通块单独处理
        Rd D=C[i].D,U=C[i].U;j=i;
        while(j<n&&C[j+1].D<=U)++j,U=max(U,C[j].U);
        ans+=sakura(D,U,Simpson(D,U));
    }
    printf("%.3lf",ans);
}