hdu1521 排列组合(指数型母函数)

题意： 有n种物品，并且知道每种物品的数量ki。要求从中选出m件物品的排数。         （全题文末）

知识点：

普通母函数

指数型母函数：（用来求解多重集的排列问题）

n个元素，其中a1，a2，····，an互不相同，进行全排列，可得n!个不同的排列。

若其中某一元素ai重复了ni次，全排列出来必有重复元素，其中真正不同的排列数应为 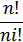，即其重复度为ni!

同理a1重复了n1次，a2重复了n2次，····，ak重复了nk次，n1+n2+····+nk=n。

对于这样的n个元素进行全排列，可得不同排列的个数实际上是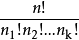

若只对其中的r个元素进行排列呢，那就用到了指数型母函数。

构造母函数G(x)=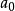+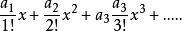则称G(x)是数列a0,a1…an的指数型母函数。

一般过程：

1.建立模型：物品n种，每种数量分别为k1,k2,..kn个，求从中选出m个物品的排列方法数。

2.构造母函数：G(x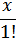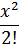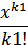)=(1+ 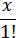+ 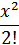…+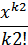)(1+ ++…)…(1+ ++…)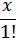

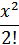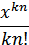=a0+a1·x+ 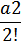· 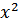+ 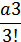· 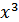+… 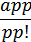· 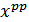（其中pp=k1+k2+k3…kn）

G(x)含义：ai为选出i个物品的排列方法数。

若题中有限定条件，只要把第i项出现的列在第i项的式中，未出现的不用列入式中。

如:物品i出现的次数为非0偶数，则原式改为…*(   + +     )*…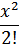

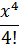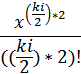题解：

标准指数型母函数题。

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long LL;
double a[15],b[15],num[15];

double jiecheng(int n)
{
    double ans=1.0;
    for(int i=1;i<=n;i++)
        ans*=i;
    return ans;
}

int main()
{
    int n,m;
    while(cin>>n>>m){
    for(int i=1;i<=n;i++)
        cin>>num[i];
    memset(a,0,sizeof(a));
    memset(b,0,sizeof(b));
    //a[0]=1.0;
    for(int i=0;i<=num[1];i++)
        a[i]=1.0/jiecheng(i);
    for(int i=2;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k<=num[i]&&j+k<=m;k++)
            {
                b[j+k]+=a[j]/jiecheng(k);
            }
        }
        for(int j=0;j<=m;j++)
        {
            a[j]=b[j];
            b[j]=0;
        }
    }
    printf("%.0lf\n",a[m]*jiecheng(m));
    }

}

排列组合

Time Limit:1000MS     Memory Limit:32768KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

有n种物品，并且知道每种物品的数量。要求从中选出m件物品的排列数。例如有两种物品A,B，并且数量都是1，从中选2件物品，则排列有"AB","BA"两种。

Input

每组输入数据有两行，第一行是二个数n,m(1<=m,n<=10)，表示物品数，第二行有n个数，分别表示这n件物品的数量。

Output

对应每组数据输出排列数。(任何运算不会超出2^31的范围)

Sample Input

2 2 1 1

Sample Output

2