[Luogu P2341] [HAOI2006]受欢迎的牛 (缩点+bitset)

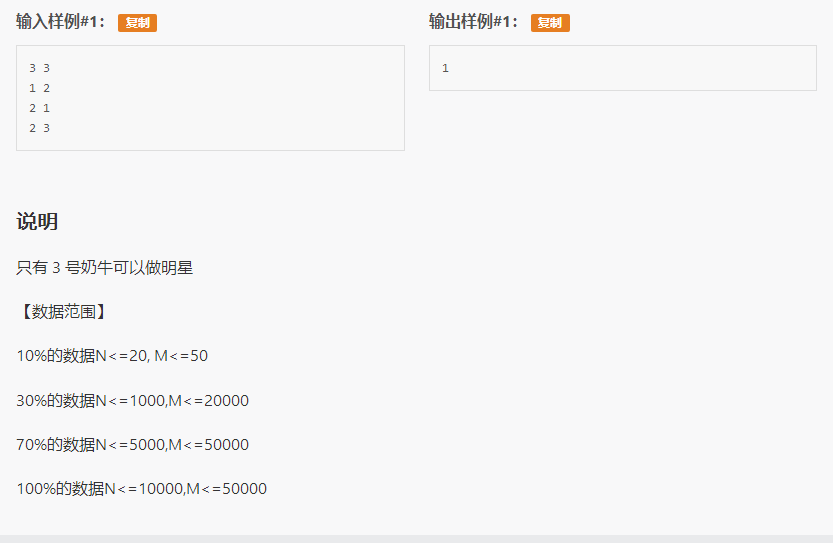
题面

传送门：https://www.luogu.org/problemnew/show/P2341

---

Solution

前排提示，本蒟蒻做法既奇葩又麻烦

我们先可以把题目转换一下。

可以把一头牛喜欢另外一头牛理解为另外一头牛被一头牛喜欢。

我们把被喜欢的关系建边，即B被A喜欢，从B向A连一条有向边。

显然，一个点若能到达其他所有节点，它就是题目中的明星牛。

接下来，我们可以考虑一个类似于DP的做法。

即一个点能访问到的点，等同于它的儿子们访问的到的点加上它自己。

显然，这种特性要在DAG（有向无环图）上才能方便的使用。

所以说，我们第一步要对题目做的是缩点。

缩完点之后，我们就可以进行图上DP了。

我们可以用一个01数组f[i][j]表示i能具体能到达的点为j（用010101数列表示）。

显然 f[i] |= f[k] （或运算）（k为i直接相连的点）

答案为f[i][j] j=11111111.... 的点

当然，这样做有一个问题。

点的最大数目为n，我们这样做是O(n^2)的，在最坏条件（没有一个点能缩在一起）的情况下，会T。

我们这时候就得请出bitset。

bitset的食用方法：https://www.cnblogs.com/RabbitHu/p/bitset.html（借用胡小兔dalao的博客）

使用bitset后，我们计算一个点能到达其他的点的复杂度一下子降为了O(n/32)

总复杂度为O(n^2/32) 

然后就可以过啦。

---

Code

//Luogu P2341 [HAOI2006]受欢迎的牛
//June,5th,2018
//缩点+（完全没必要的）bitset
#include<iostream>
#include<cstdio>
#include<vector>
#include<stack>
#include<bitset>
using namespace std;
long long read()
{
    long long x=0,f=1; char c=getchar();
    while(!isdigit(c)){if(c=='-') f=-1;c=getchar();}
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x*f;
}
const int  N=10000+100;
vector <int> e[N],e2[N];
int n,m,belong[N],nd_tot,dfn[N],mcount,low[N],cnt[N];
bool InStack[N];
stack <int> s;
bitset <N> arrival[N];
void Tarjan(int now)
{
    InStack[now]=true;
    s.push(now);
    dfn[now]=low[now]=++mcount;
    for(int i=0;i<int(e[now].size());i++)
        if(dfn[e[now][i]]==0)
        {
            Tarjan(e[now][i]);
            low[now]=min(low[now],low[e[now][i]]);
        }
        else if(InStack[e[now][i]]==true)
            low[now]=min(low[now],low[e[now][i]]);
    if(low[now]==dfn[now])
    {
        nd_tot++;
        while(s.empty()==false)
        {
            int temp=s.top();
            s.pop();
            InStack[temp]=false;
            belong[temp]=nd_tot;
            cnt[nd_tot]++;
            if(temp==now) break;
        }
        arrival[nd_tot][nd_tot]=true;
    }
}
bool vis[N];
int ans=0;
void dfs(int now)
{
    vis[now]=true;
    for(int i=0;i<int(e2[now].size());i++)
    {
        if(vis[e2[now][i]]==false)
            dfs(e2[now][i]);
        arrival[now]|=arrival[e2[now][i]];
    }
    if(int(arrival[now].count())==nd_tot)
        ans+=cnt[now];
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;i++)
        e2[i].reserve(4),
        e[i].reserve(4);
    for(int i=1;i<=m;i++)
    {
        int s=read(),t=read();
        e[t].push_back(s);
    }

    for(int i=1;i<=n;i++)
        if(dfn[i]==0)
            Tarjan(i);
    for(int i=1;i<=n;i++)
        for(int j=0;j<int(e[i].size());j++)
            if(belong[i]!=belong[e[i][j]])
                e2[belong[i]].push_back(belong[e[i][j]]);
    for(int i=1;i<=nd_tot;i++)
        if(vis[i]==false)
            dfs(i);

    printf("%d",ans);
    return 0;
}

正解（C++）